非古典邏輯:直覺主義
布勞威爾 (1881 – 1966)是最早脫離所謂「古典邏輯」系統的學者之一。他反對弗雷格和羅素將數學化約為邏輯的構想,認為數學根基於我們對某些基本數學物件(如數字和直線)的「直覺」,因此他的學說便稱為「直覺主義」。
 直覺主義。圖/大話題:邏輯
直覺主義。圖/大話題:邏輯惡魔論證
布勞威爾主要將焦點擺在無限集合和序列上,例如所有正數的集合和無理數(如 π 和)小數點後的數字形成的序列等等。他的論證大致如下:
我邏輯上能證明 666 這個序列一定會出現在任何無理數(如 π)的擴張裡。因為若主張 666 不在裡面,就代表 666 不出現在 π 的小數點後數字的任何地方,但這一點在數學上是無法證明的。就算世界上所有白紙都寫滿π的小數點後數字,還是有無限多的數字沒檢查到。
 惡魔論證。圖/大話題:邏輯。
惡魔論證。圖/大話題:邏輯。直覺邏輯的興起
雖然布勞威爾只想證明有些數學證明的方式和邏輯證明不同,但有些人發現他的論證也能用來證明某些數學領域的邏輯和其他數學領域不同,甚至有些人還據以建構出一套邏輯系統,並嘗試證明這套邏輯適用於所有數學領域。這套系統就叫「直覺邏輯」。
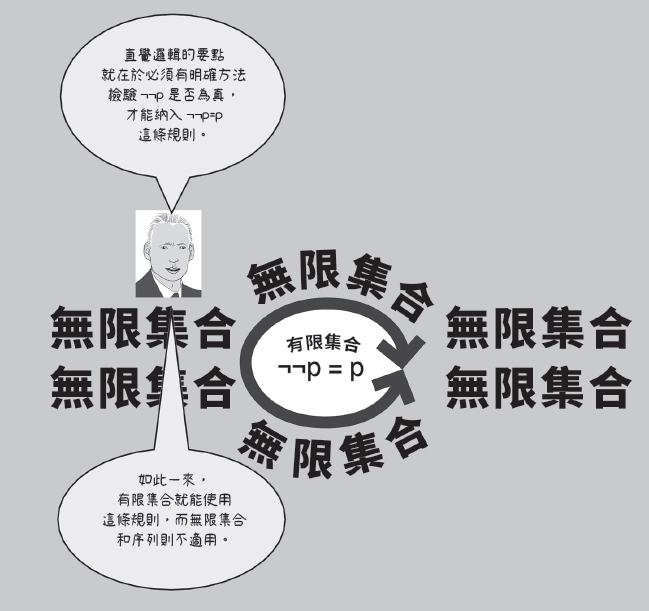 直覺邏輯系統。圖/大話題:邏輯。
直覺邏輯系統。圖/大話題:邏輯。直覺主義 v.s. 歸謬法
直覺邏輯有一個關鍵特點,就是不能用萊布尼茲的歸謬法。歸謬法是先假設某個數學陳述的否定為真,然後導出矛盾,進而證明該陳述為真。但要從「某事的否定為假」推導出「某事為真」就得仰賴排中律,因此在某些數學領域裡,歸謬法並不符合數學應該運作的方式,也就是從公理推導出數學語句。
 直覺邏輯與歸謬法互相對立。圖/大話題:邏輯。
直覺邏輯與歸謬法互相對立。圖/大話題:邏輯。直覺主義的數學熱潮
上述問題在 1930 年代引發了一波新的數學熱潮,不少學者嘗試用直覺邏輯替一些常用的基本數學陳述找到證明,也確實找到了不少。
數學系和哲學系紛紛成立,新的學術領域也隨之誕生。就連希爾伯特的方法明明是直覺邏輯的對手,也被加以改造,只使用得到認可的直覺主義程序。直到這股風潮引起了哥德爾的注意。
儘管後來學者對這場爭辯的興趣削弱了一些,但「唯有構造性證明才能確保一個陳述句為真」的基本看法至今仍然得到不少邏輯學家、數學家、科學家和哲學家支持。
 許多人試著用直覺邏輯替數學陳述找證明。圖/大話題:邏輯。
許多人試著用直覺邏輯替數學陳述找證明。圖/大話題:邏輯。
處理未來陳述句的老問題
大約同一時期,波蘭數學家盧卡西維茨(1897 – 1956)1920 年提出的構想勾起了一些學者的興趣。此前十多年,這個構想從來不曾在波蘭以外的地區引起多大反應。盧卡西維茨當時想解決的,是從亞里斯多德到羅素都面對過的老問題。
編按:「如何判斷大笨鐘一千年後會遇上大雪」這句話的真值?
 未來陳述句是邏輯無法確認之事。圖/大話題:邏輯。
未來陳述句是邏輯無法確認之事。圖/大話題:邏輯。



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


