重複賽局中的均衡結果
在 1883 年,法國經濟學家伯特蘭(1822 – 1900)研究了販售相同產品的廠商之間的價格競爭,在他的分析中,廠商面對的誘因問題很類似囚徒困境賽局。
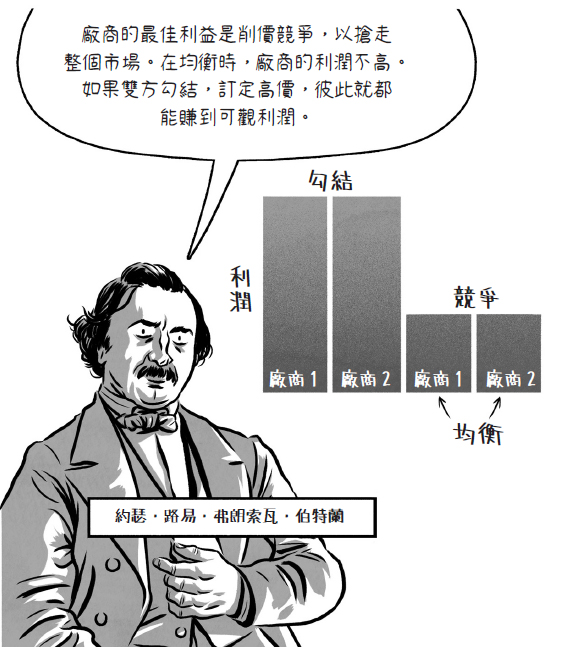 削價競爭是不同廠商間達到均衡的可能。圖/《大話題:賽局理論》
削價競爭是不同廠商間達到均衡的可能。圖/《大話題:賽局理論》伯特蘭預測在均衡時廠商之間會彼此削價,類似囚徒困境賽局中的{認罪,認罪}結果。但我們在現實中常常看到廠商彼此勾結並訂定高價。西方民主國家多數立有「反壟斷法」禁止這類勾結,以促進競爭。
為了瞭解在囚徒困境之類的處境中,參與者何時會勾結,我們必須跳脫一次性賽局,也就是參與者只進行一次後就結束的賽局。轉而考慮更符合現實的重複互動,也就是參與者會不斷進行同樣賽局。
 為避免削價競爭,廠商間可能會想透過合作訂出更好的價格。圖/《大話題:賽局理論》
為避免削價競爭,廠商間可能會想透過合作訂出更好的價格。圖/《大話題:賽局理論》如果參與者重複互動,我們能夠在囚徒困境中觀察到合作的均衡嗎?
假設兩位參與者都知道囚徒困境賽局會進行兩次。為了找出重複互動賽局的均衡,我們要先預測最後一回合賽局的均衡,然後倒推第一回合賽局的均衡。這種推理方式稱為逆向歸納法。
 預測下一次均衡的賽局來回推這次該採取的行動。圖/《大話題:賽局理論》
預測下一次均衡的賽局來回推這次該採取的行動。圖/《大話題:賽局理論》如果這就是結局?
在第二回合,參與者知道這是最後一次互動,也就沒有必要嘗試改變未來的結果。因此,最後一局結果就像是一次性囚徒困境:沒人合作。
參與者可以推論,不論第一回合如何,第二回合肯定沒有合作。那麼,從參與者的角度來看,第一回合也跟一次性囚徒困境沒有兩樣。因此,在均衡時兩回合都不會出現合作。
事實上,即使囚徒困境賽局進行多次,只要賽局有個確切的結束回合,我們永遠不會觀察到合作。逆向歸納法從最終回合拆解了整體賽局的結果。
 由於預測到結局,因此人們選擇不再合作了。圖/《大話題:賽局理論》
由於預測到結局,因此人們選擇不再合作了。圖/《大話題:賽局理論》現實世界沒有真正的「最終回」
以色列裔美國數學家歐曼(1930 年生)在 2005 年與謝林一起獲得諾貝爾經濟學獎。他的研究之一是無限回合賽局均衡下的合作行為。在無限回合中,逆向歸納法無法從最終局拆解合作情形,因為沒有明確的最終局。
合作要能成為均衡的結果,首要條件是參與者的策略能夠處罰過去的壞行為(不合作)。為了避免以後受罰,參與者可能選擇合作。
 此刻的合作將影響到未來自我的利益時….圖/《大話題:賽局理論》
此刻的合作將影響到未來自我的利益時….圖/《大話題:賽局理論》試看在無限回合的囚徒困境賽局中所謂的冷酷策略:參與者起初採取合作行動(例如囚徒保持沉默,也可能是室友賽局中的洗碗,或是廠商的勾結高價)。
在接下來的賽局中,只要對方合作,我也一直保持合作。但只要對方背叛了(例如囚徒認罪、室友不再洗碗、廠商用低價搶走市場),我就選擇背叛。
 此時的合作是怕雙方不合作的結果。圖/《大話題:賽局理論》
此時的合作是怕雙方不合作的結果。圖/《大話題:賽局理論》





 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


