強大的三角測量學！讓我們先回顧簡單的三角邊比——《數學大觀念》

三角學能讓我們解出一些無法用古典幾何學處理的幾何題目，舉例來說，考慮下面這個問題：

僅用一個量角器和一個袖珍計算機，測出附近某座山的高度。

對於這個問題，我們將提出五種不同解法。實際上，前三種解法幾乎連一丁點數學都沒用上！

方法一（費力解法）

爬上山頂，將你的計算機往下丟（這可能需要用上相當大的力氣），然後測出計算機撞到地面所需的時間（或聆聽下方背包客的尖叫聲）。如果總共花費了 t 秒，且忽略空氣阻力和終端速度帶來的影響，那麼標準的物理學方程式會指出這座山大約高 16t2 英尺。

這個方法的缺點是空氣阻力和終端速度的影響可能相當大，所以你的計算會變得不精確，而且要找回這台計算機也不太可能了。除此之外，這個方法需要用到的計時器可能就在你的計算機上。要說優點的話，則是這個方法並不需要用到量角器。

方法二（輕鬆解法）

找一位友善的保育巡查員，然後用你的嶄新量角器跟他交換山峰的高度這項情報。如果你找不到任何保育巡查員，那就看看附近有沒有一位親切的男士，他一身漂亮的古銅色肌膚表示他可能花了很多時間待在戶外，因而可能對你這個問題的答案相當清楚。

這個方法的優點是你有可能會交到新朋友，而且不需要犧牲你的計算機。此外，如果你對這位深膚色男士的回答心存懷疑，你還是可以親自爬上這座山，然後採用第一個方法找出答案。這個方法的缺點是你可能會失去你的量角器，還被冠上賄賂的罪名。

方法三（聰明解法）

在嘗試方法一和方法二之前，先試著找出一個告示牌，上面標有這座山的高度。這麼做的好處是你不需要犧牲任何一項裝備。

當然，如果這三種方法都不合你意，那麼我們就必須訴諸於數學的解法，也就是本章的主題。

研究三角形可以做什麼？

「三角學」（trigonometry）在字面上就是三角測量的意思，這個詞的字根源自希臘文「trigon」和「metria」。接下來我們先從分析一些經典的三角形開始。

等腰直角三角形

等腰直角三角形包含一個 90º 角，它的另外兩個角必定相同，所以兩者都是 45º（因為三角形的內角和為180º），這樣的三角形我們稱之為 45−45−90 三角形。如果兩個直角邊的長度都是1，那麼根據畢氏定理，斜邊長一定是 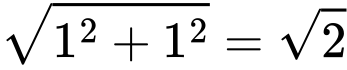。請注意，任何等腰直角三角形的邊長比例都是 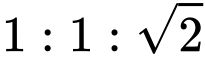，如下圖所示。

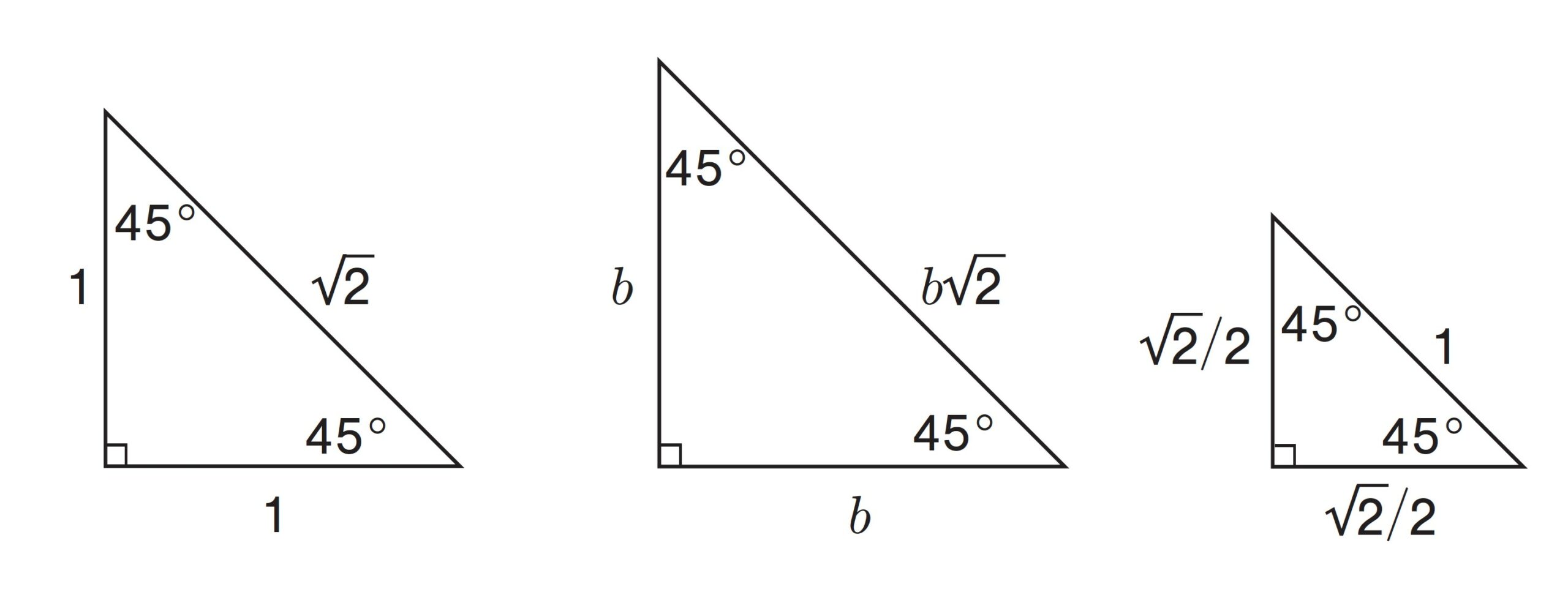在一個 45−45−90 三角形中，邊長的比例是 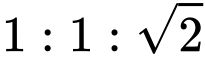。圖／數學大觀念

30− 60− 90 三角形

在一個等邊三角形中，每個邊長都相同，而且每個角的大小都是 60º。如果我們將一個等邊三角形分成全等的兩半，如下圖所示，就會得到兩個其內角分別是 30º、60º 和 90º 的直角三角形。如果這個等邊三角形的邊長為 2，那麼內含的兩個直角三角形的斜邊長就會是 2，而較短的直角邊長為 1。根據畢氏定理，較長的直角邊長會是。因此，所有 30− 60− 90 三角形的比例都會是 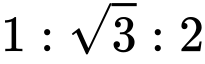（也可以學學我，用 1、2、 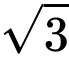這個簡單的順序來記憶）。特別是如果斜邊長為 1，則另外兩個邊長分別是 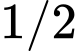以及 。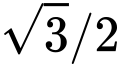

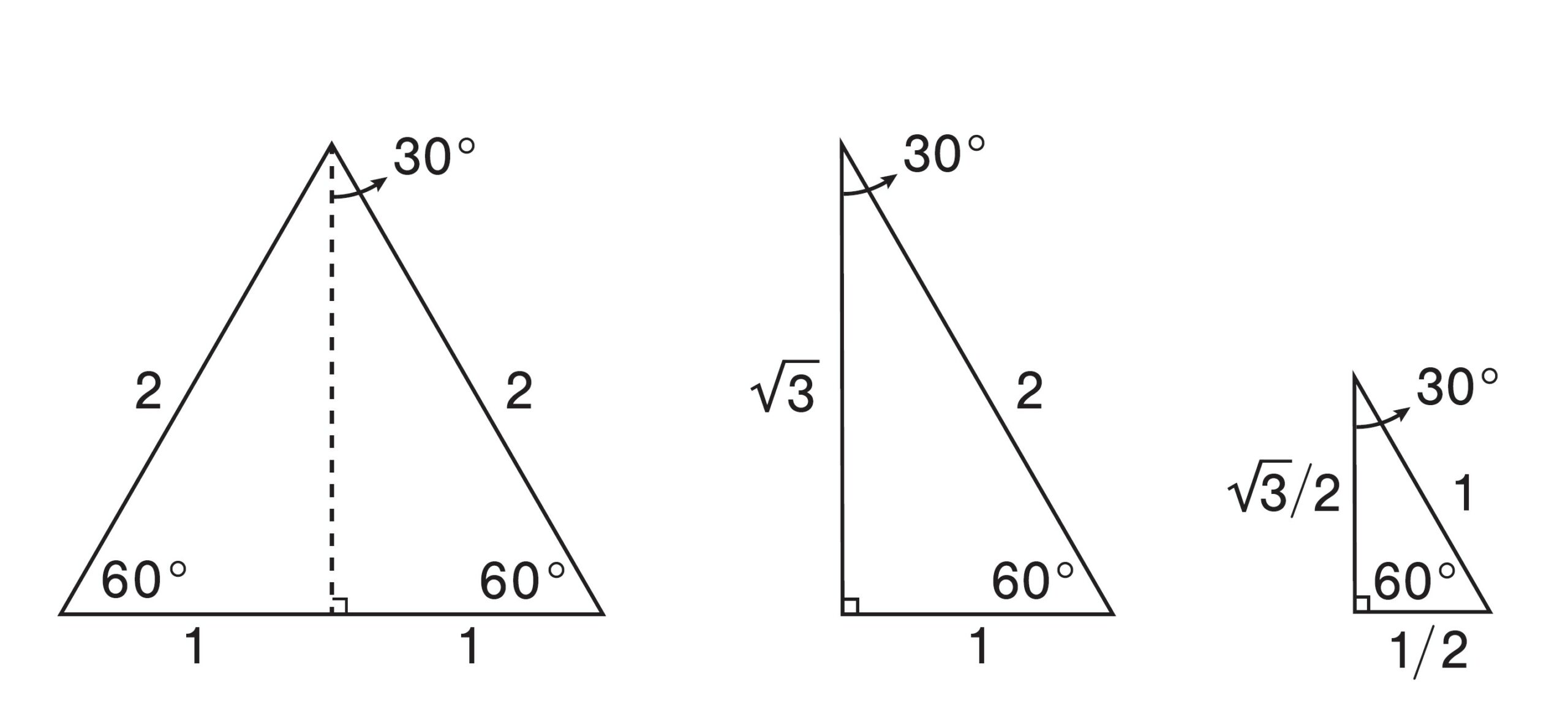在一個 30− 60− 90 三角形中，邊長的比例是 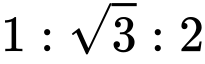。圖／數學大觀念

——本文摘自《數學大觀念：全面理解從數字到微積分的12大觀念》，2023 年 3 月，貓頭鷹出版，未經同意請勿轉載。

Read More