【数学】数学规划简介

前言

数学规划(mathematical programming)，也称数学优化(mathematical optimization)，是数学中的一个分支，它主要研究的目标在给定的区域中寻找可以最小化或最大化某一函数的最优解。数学规划在几乎所有的科学领域都有着不容忽视的应用，所以一直都是一门受到着重关注和研究的学科。本文是对数学规划问题的一个浅显的介绍，不涉及任何理论和算法。

数学规划

一个数学规划问题一般具有以下形式
\text{min}  &&f(x)\\
\text{s.t.} &&c_i (x) \le b_i, i=1,\dots,k  \\
&&x\in \mathbb{R}^n\text{min}  &&f(x)\\\text{s.t.} &&c_i (x) \le b_i, i=1,\dots,k  \\&&x\in \mathbb{R}^n

在这里面，函数 �:��→�,��:��→�,��∈�。函数 f 是我们想最小化的目标函数(objective function)；而函数 �� 和常量��则对可行集构成一些限制，不等式 ��(�)≤��叫做一个约束(constraint)，所有满足这些约束的点的集合

Ω={�∈��:��(�)∈��,�=1,…,�}

被称作这个问题的可行区域(feasible region)。

我们看一下实际应用中的问题是如何以数学规划的方式表达。假设呢，现在我们有两种金融资产可以进行选择，第一个资产平均每年有 10% 的收益，但是在最坏情况下可能损失 20%；第二个资产每年平均有 5% 的收益，但最大损失也不会超过 5%。方便起见，假设这两个资产是可以无限拆分的，也就是说我们可以买 1/2 个或者 ��1+5个。现在假设我们有本金 100，可以投资于这两个资产；我们希望在最坏的情况下损失不超过本金的 10%，也就是 10，目标嘛，当然是要最大化预期收益率。

好哟。首先确定我们的问题，是这两种资产要各配置多少钱。那么，这个问题所在的空间是 �2，对于里面的一个向量 x，坐标 �1 和 �2分别是两种资产购买的净值。其次，我们想最大化的是预期收益，也就是

�(�1,�2)=0.1�1+0.05�2

有两个要求。第一个是购买的资产总值不可以超过起始资金 100。让 �1 代表两种资产价值总和的函数， �1 代表总值产100，有�1(�1,�2)=�1+�2≤100=�1

还有呢，最坏情况下损失不可以超过 10，那么设 �2 为最大损失的函数，设 �2 等于 10，有�2(�1,�2)=0.1�1+0.05�2≤10=�2

好，新鲜的规划问题就出炉了：\text{max} &&0.1x_1+0.05x_2\\
\text{s.t.} &&x_1+x_2 \le 100\\
&&0.1x_1+0.05x_2 \le  10\text{max} &&0.1x_1+0.05x_2\\\text{s.t.} &&x_1+x_2 \le 100\\&&0.1x_1+0.05x_2 \le  10

当然，也可以写成矩阵的形式

\text{max} &&\begin{bmatrix}
0.1\ \ 0.05
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}\\
\text{s.t.} &&\begin{bmatrix}
 &1&1\\
&0.2&0.05
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}\le
\begin{bmatrix}
100\\
10
\end{bmatrix}\text{max} &&\begin{bmatrix}0.1\ \ 0.05\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}\\\text{s.t.} &&\begin{bmatrix} &1&1\\&0.2&0.05\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}\le\begin{bmatrix}100\\10\end{bmatrix}

格式上的细节:

• 你说，啊，教程里都是骗人的。说好了的最小化 f(x)，为什么上面的问题是最大化呢？
• 不，我才不会骗小孩。

上面的问题是可以转换成最小化问题的，只需要在目标函数前加上一个负号，最大化 f(x) 和最小化 −f(x) 是等同的，如果 (�1∗,�2∗)是 −f 的最小解，那么它也必定是 f 的最大解。同理的，如果有大于号的限制
��(�)≥��

加上负号就可以转换为等同的小于号限制

−��(�)≤−��

另外，如果我们需要等于号的限制

��(�)=��

也可以将它转换为一个大于一个小于两个限制的交集

��(�)≤����(�)≥��

第二个大于有可以转变成小于

c_i(x) &&\le b_i\\
-c_i(x) &&\le -b_ic_i(x) &&\le b_i\\-c_i(x) &&\le -b_i

同样变成了上面的标准格式。

经过这些转换的技巧，标准格式
\text{min} &&f(x)\\
\text{s.t.} &&c_i (x) \le b_i, i=1,\dots,k\text{min} &&f(x)\\\text{s.t.} &&c_i (x) \le b_i, i=1,\dots,k

实际上可以表达各种各样的问题。对于单独的问题，我们一般会以最方便的方式写出来，用大于号、等于号或最大化都没有关系；但在整体地研究优化理论时，一般会用统一的问题格式，这样研究和推导的过程会更方便。

规划问题的分类

数学规划问题可以分为很多很多种类，这里我们将介绍四个最常用到的类别。这四类问题并不是并列关系，而是（很大程度上的）包含关系，其中更小的类别会包含更少的问题，但是由于这些问题普遍有着同样的结构和性质，在这个类别中会有一致受用高效算法；而更大的类别会包含更多的优化问题，但是由于缺乏良好的函数结构，解决起来一般会更麻烦。

• 线性规划

如果一个规划问题的目标函数 f 和约束函数 �� 都是线性函数，我们说它是一个线性规划(linear programming)问题。线性规划都可以写成矩阵的形式：
\text{min} &&c^Tx\\
\text{s.t.} && Ax \le b\\
&&x\in\mathbb{R}^n\text{min} &&c^Tx\\\text{s.t.} && Ax \le b\\&&x\in\mathbb{R}^n

这里，�∈��,�∈��×�并且�∈��。第2节中举的例子就是一个线性规划问题。

线性函数是在实数域上最容易分析的一类函数，它们有很强的结构性，直线嘛，从哪里看都是一模一样的。也正是因为如此，解决线性规划问题也相对简单，所有线性规划问题都可以在多项式时间内找到最优解。

• 二次规划

满足以下格式的规划问题都被称作二次规划(quadratic programming)：
\text{min} && \frac{1}{2}x^T Q x + c^Tx\\
\text{s.t.} && Ax \le b\\
&&x\in\mathbb{R}^n\text{min} && \frac{1}{2}x^T Q x + c^Tx\\\text{s.t.} && Ax \le b\\&&x\in\mathbb{R}^n

这里，�∈��×� 是一个对称矩阵（也就是说 ��=�）， �∈��， �∈��×� 还有 �∈��。二次规划比线性规划多出了一个����项，也是由矩阵的乘积表示的，所以虽然不是线性函数，但是仍可以使用很多线性代数的技巧进行分析。二次规划问题的难度取决于矩阵 Q：如果 Q 是正定矩阵（所有的特征值都大于 0），那么可以在多项式时间内找到最优解；如果 Q 是不定的（有小于 0 的特征值），寻找最优解一般是 NP-难的。

应该指出，任何一个线性规划问题都是二次规划问题 — 将二次项的 Q 设成零矩阵即可。

• 凸规划

讲到凸规划，我们应该先了解凸函数什么。如果�:��→� 是一个连续函数，并且对于任何 x, ��∈�� 以及�∈[0,1]，满足

�(��+(1−�)�′)≤��(�)+(1−�)�(�′)

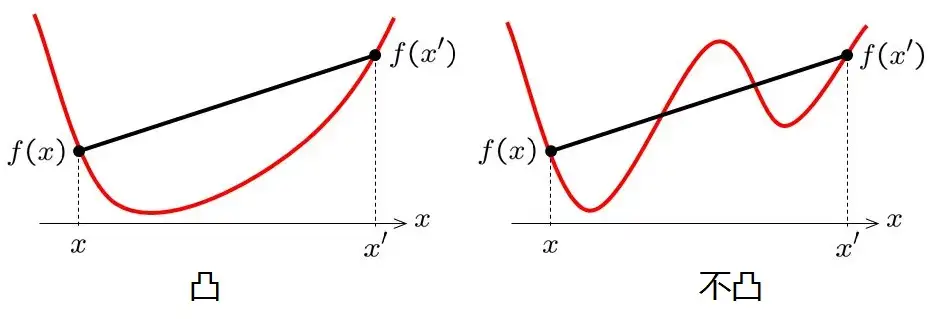
我们说 ff 是一个凸函数(convex function)。在直观的理解上，就是在这个函数的图上的任意连点之间连一条直线，这个函数不会超过这条直线。

那么，如果在一个规划问题中，

\text{min}  &&f(x)\\
\text{s.t.} &&c_i (x) \le b_i, i=1,\dots,k  \\
&&x\in \mathbb{R}^n\text{min}  &&f(x)\\\text{s.t.} &&c_i (x) \le b_i, i=1,\dots,k  \\&&x\in \mathbb{R}^n

函数 f 和 �� 都是凸的，我们说它是一个凸规划(convex programming)问题。凸函数有什么好处呢，我们举一个形象的例子：在上面的两个函数曲线（红色）上，我们在 f(x′) 的位置放一个圆珠，让它自己滚下去。在第一个凸函数里，圆珠会一路滚下去并停在整个函数的最低点；而在第二个不凸的函数里，圆珠会停在右边的局部低点里，却到不了全局的最低点。从这可以看出，如果 f 是凸函数，寻找它的最低点会更容易。但即便如此，很多凸规划问题的最优解还是 NP-难的。

对于一个二次规划问题，如果二次项的矩阵 Q 是半正定的，那么它也是一个凸规划问题；但是如果 Q 是不定的，那么二次目标函数并不是一个凸函数。

• 非线性规划

非线性规划是一个非常大的问题类型，一般来说，如果规划问题中
\text{min}  &&f(x)\\
\text{s.t.} &&c_i (x) \le b_i, i=1,\dots,k  \\
&&x\in \mathbb{R}^n\text{min}  &&f(x)\\\text{s.t.} &&c_i (x) \le b_i, i=1,\dots,k  \\&&x\in \mathbb{R}^n

函数 f 和 �� 都是连续的，它就是一个非线性规划(non-linear programming)问题。也许这个类别的名字起得有点不恰当，因为线性规划问题其实也属于非线性规划问题，而这个“非”字可以这么理解：线性规划是非线性规划中极其小的一部分，如果我们有一个线性规划问题，那么用线性规划的方法就可以很简便地解决，并不需要非线性规划的理论，所以非线性规划实际研究的是线性规划以外的问题。

非线性规划的涉及面太广，以至于很多未解的数学难题都可以写做为非线性规划的形式，可见普遍的非线性规划问题有多难。因此，在研究非线性规划问题时，我们一般会加上一些额外的条件限制，比如：目标函数 f 是可导的或是平滑的、 f 或 f 的导数是 Lipschitz 的、问题的可行区域是凸的，等等。不难看出，上面的所有其他类别的规划问题都属于非线性规划问题。

结语

本文概括性地介绍了数学规划的基本内容和一些问题的分类。在量化课堂未来的文章中，我们将介绍各类规划问题的数学理论、解题算法以及应用方法，敬请期待。