大家都知道「地球在動」，但你怎麼知道？

623次阅读

没有评论

賴昭正／前清大化學系教授、系主任、所長；合創科學月刊

在第一本書中，我將描述球體的所有位置，以及我歸因於地球的運動，因此本書可以說是包含宇宙的一般結構。在剩餘的書中，我將其它恆星和所有球體之運動與地球的移動性聯繫起來，這樣就可以確定如果歸因於地球的運動，它們的運動和外觀可以保存到什麼程度。

－哥白尼（Nicolaus Copernicus，1473 – 1543）

隨便找個國中生問：「地球是宇宙的中心嗎？」相信他們都會回答說：「不是。地球除了自轉外，還在繞著太陽公轉。」可是如果你緊接著問：「你怎麼知道它在動呢？」相信大部分的國中生（甚至大學生）可能就不知道怎麼回答了：「嗯⋯這？⋯那？⋯？？」

這事實上是一個非常難以回答的問題，因此雖然早在公元前 250 年希臘天文數學家阿里斯塔克斯（Aristarchus ，公元前 310 – 230）就曾經提出地球繞日說，但這一理論不但不為大眾所接受，還給他帶來了一生的嘲笑。

而希臘數學家蛇床子（Eudoxus of Cnidus，公元前 410 – 347）於公元前 380 年左右提出以不動之地球為中心的宇宙模型則幾乎統領了以後 2000 年的宇宙觀！

你該如何證明地球自轉？圖／envatoelements。

1543 年，波蘭哥白尼基於在數學上處理起來比較簡潔，在德國紐倫堡出版六本題為《De Revolutionibus Orbium Coelestium》（論天體運轉）之書，提出日心系統，謂地球不在宇宙中心之特別位置，而是與其它行星一起在圍繞太陽的圓形軌道上運動。

此後經伽利略（Galileo Galilei，1564 – 1642）、開普勒（Johannes Kepler 1571 – 1630）、及牛頓（Isaac Newton,1643 – 1727）等天文數學家的發展，地球繞日說不但慢慢地為天文學家所接受，也漸漸成為主流的宇宙觀。但這些發展似乎都是紙上談兵而已，並不是真正的觀察實驗結果。

有什麼方法可以證明地球是在動的呢？

加速度運動

相信大部分的讀者都有下面的經驗，那就是坐在平穩（等速）直線行駛的車廂內不會覺得火車在動；如果那個時候旁邊也有一輛類似的火車經過，我們根本無法知道到底是誰在動。

事實上不止不會覺得火車在動，伽利略早在四百多年前就告訴我們：不管在車廂裡做任何實驗都沒有辦法偵測出火車在動的（相對論）。但是如果火車突然加速，我們便可立即警覺到火車在動。

如果坐在等速前進的火車中你不會感受到火車在動。圖／envatoelements。

圓周運動因為運動方向一直在改變，所以不是直線運動，而是一種加速度運動。坐遊樂場所裡的旋轉木馬之所以有被往外甩的感覺便是因為加速度造成的。地球的自轉及公轉都是圓周運動，我們不是也應該有被往外甩的感覺嗎？

高中物理告訴我們圓周運動的加速度 a 為

大家都知道「地球在動」，但你怎麼知道？

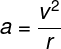
上式中的 v 為圓周上物體的運動速度，r 為圓半徑。地球自轉運動最厲害的地方在赤道上, 將其值及地球半徑代入上式，得地球自轉在赤道上的加速度為 0.033 m/s2，只有重力加速度 9.8 m/s2 的 300 分之 1 而已。

這加速度需要 14 分鐘才能將車子或火車從零加速到時速 100 公里（「高性能」車子大約只需十秒鐘），我們能感覺出來嗎？此一往外甩的慣性力【常被稱為「離心力」（centrifugal force）】與重力方向相反，因此如果有非常精確的體重機，原則上可以讓我們測出赤道上重量減輕，證明地球在自轉的。

將地球公轉的平均速度及半徑代入上式，則得地球公轉的加速度為 0.006 m/s2，與重力加速度一比更是微乎其微。所以想靠地球自轉及公轉的加速度來偵測地球在動顯然是相當困難的。

恆星視差

坐火車的人都有這一經驗：窗外比較近的東西從眼前飛過，越遠的東西就越不動。所以如果火車是從左往右，當你比較圖一中遠近不同之 A、B 兩點的相對位置時，你將發現中非常遠的 A 點不動；但是比較近的 B 點則會從 A 之右邊 B’ 移到 A 之左邊 B”。事實上這視差與火車動不動無關，而是因 A、B、及觀察者三者的相對位置而異。

圖／作者提供

同樣的道理，因為地球繞太陽公轉，我們可以在兩個不同的軌跡點（例如夏至及冬至兩點）看到這「恆星視差」（stellar parallax）現象（圖一）。1838 年，德國天文學家貝塞爾（Friedrich Bessel）成功測量了天鵝座（Cygni）61 號恆星的視差，證明地球並不是一年四季都在同一個位置。當然，不在同一個位置表示「動過」，所以間接地證明了地球在動。

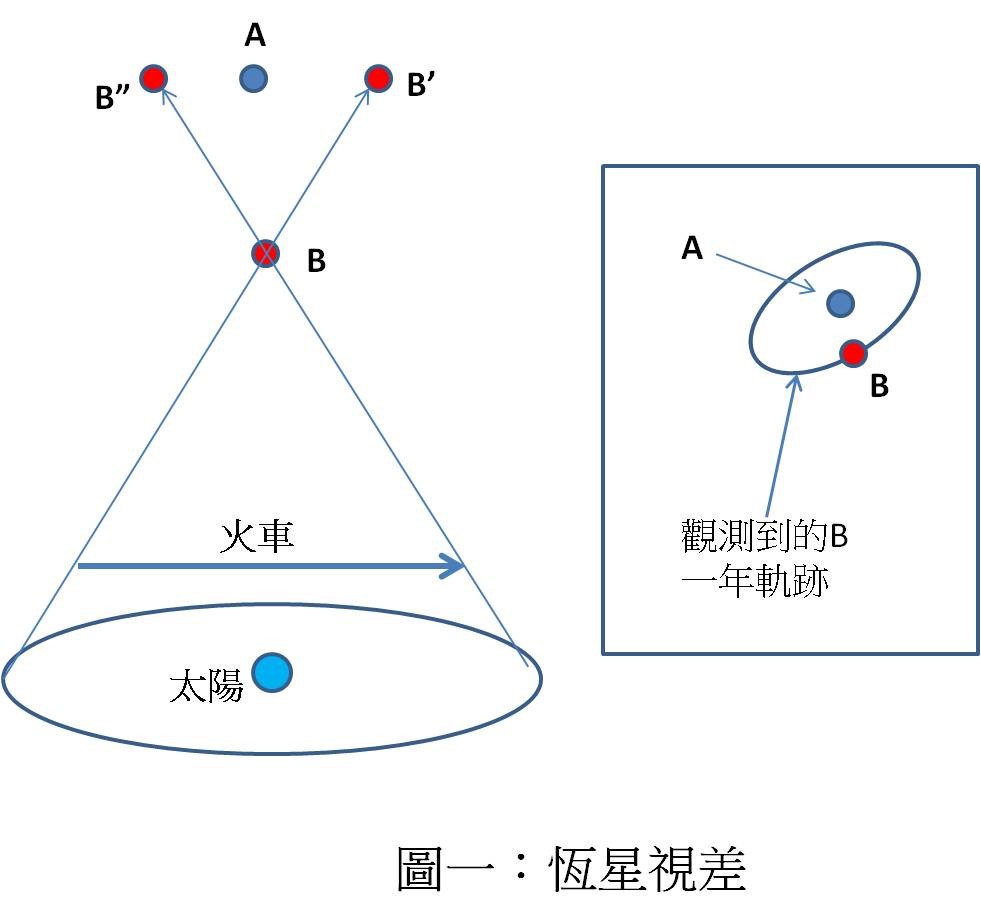
星光像差

站在大雨筆直而下的大街上時，你只需將雨傘直接舉過頭頂即可保持乾爽。可是當你開始走路時，你便必須將雨傘朝行走方向傾斜以免被淋濕，走得越快，傾斜度就需要越大。如果不知道雨是垂直而下（對地球而言），你將誤以為雨是從前方傾斜而至（對你而言）。

（左）在雨中靜止不動；（右）在雨中往右跑。圖／作者提供

同樣的道理。當地球繞太陽公轉運動時，我們也可以檢測到與運動速度有關之入射星光的「傾斜」（見圖二）——在天文學上稱為「星光像差」（stellar aberration）。因為地球一年四季的運動速度不同，所以「像差」也將因之而異。。

1725 年起，英國天文學家布拉德利（James Bradley）及同事一直在努力想測量天龍座伽馬（Gamma Draconis）的視差；他們雖然沒有找到預期的現象，但卻發現天龍座伽馬在三天內往「錯誤」的方向移動了驚人的弧度。在同事去世後不久，布拉德利終於意識到這無法用視差來解釋的現象是：因地球在恆星方向運動速率不同之「光像差」（light aberration）和光速有限所引起的。

布拉德利於 1729 年元月向英國皇家學會宣布此一首次確鑿證明地球在「動」的發現，提供了阿里斯塔克斯、哥白尼、和開普勒理論正確性的觀察證據。巴黎天文台台長德蘭布爾（Jean Delambre）認為這是「（18 世紀）最輝煌、最有用的發現」；在其 1821 年所出版之《18 世紀天文學史》中謂：「正是由於布拉德利的這⋯發現，我們才有了現代天文學的準確性。」

圖／作者提供

傅科

最能夠直接證明地球每日自轉的實驗是「傅科擺」（Foucault pendulum）。法國人傅科（Léon Foucault，1819 – 1868）小時候對學校功課沒興趣，喜歡自己在家建造玩具和機器。1839 年進入巴黎醫學院，看到血就昏暈，因此只好放棄從醫。但指導教授多內（Alfred Donné）慧眼識英雄，把他留聘為助手從事研究，兩人於 1845 年合作出版了《顯微鏡課程》(A Course of Microscopy)。

傅科與多內的合作開啟他作為科學傳播者的職業生涯：多內退休後，傅科成為具有影響力之《辯論雜誌》(Journal de Débats ) 的科學編輯，接替了多內向公眾報導最新科學領域發展的角色。透過每週生動地報導巴黎科學院會議，傅科很快引起了公眾和科學精英的注意，包括了法國具有影響力的數學家和政治家阿拉戈（François Arago）。

圖／作者提供

1850 年傅科突發出奇想：如果能夠設計出一個鐘擺，其頂點雖可以隨地球上的支架移動，但能完全自由轉動（也就是與支架間的旋轉摩擦力為零）；那麼鐘擺一旦開始擺動，因為不會跟著地球旋轉，地球將在其下方旋轉——但對地球上觀察者來說，將是擺動平面在旋轉。1851 年元月，傅科在家中地下室成功地建造了這樣一個鐘擺後，阿拉戈要求他在巴黎天文台也裝置一個。

不久後，巴黎的每一位科學家都收到了前往巴黎天文台參觀鐘擺的邀請。在天文台進行實驗證明地球確實在旋轉的 1851 年 2 月 3 日，阿拉戈也向科學院宣讀了現在稱為「傅科擺」的論文。幾週後，傅科在巴黎萬神殿（Panthéon）的圓頂上用一根 67 米長的金屬絲懸掛了一個重 28 公斤的黃銅塗層鉛擺，又復製了一個「傅科擺」（圖三，註 1）。

傅科擺的物理

台灣早期科教館曾經展示過「傅科擺」，現在已經找不到了。但相信許多讀者都曾在世界其它各地（如北京或廣州）看過。如果在北極的正上方掛一個「傅科擺」，我們很容易直覺地了解地球將在其下方以 24 小時的週期旋轉。將鐘擺掛在赤道上某一點的正上方，則它只受到地球自轉的前進推力（見後），筆者還可以了解（看出）地球在其下方不會旋轉；但筆者很難想像掛在台北的上空時，地球如何在其下方旋轉？

在忘寢廢食之苦思後，筆者終於領悟到伽利略 1630 年用來錯誤地「證明」地球在動的例子，事實上正是解釋 1851 年「傅科擺」的最佳工具。一個往東方前進之逆時針方向旋轉輪子，在任何一瞬間，對「一位靜止不動的旁觀者 A」來說（圖四左），最上方那一點的速度應該比中間點慢，最下方那一點則比中間點快（註 2）。

但是對於與輪子同時前進、但不旋轉之中間觀察者 B 來說（圖四中），兩個向量相減的結果，上方那一點的速度將是往左，下方那一點的速度則是往右，這正是為什麼他只看到輪子在逆時針方向旋轉的原因。對一位隨輪子旋轉及前進之中間觀察者 C 來說，則輪子不轉不動：如果觀察者 B 不是一個數學點的話，將依順時針方向旋轉（圖四右，註 3）！

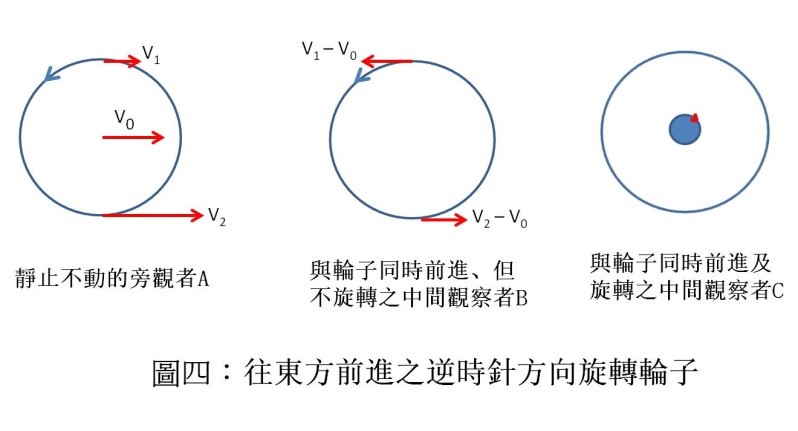圖／作者提供

地球自轉造成台北 101 大樓往右的旋轉推力；大樓南方因為旋轉圈子比正上方的中間點大，速度因之比中間點快；反之，大樓北方則因為旋轉圈子較小，速度應比中間點慢（圖五白色箭頭）。所以對旁觀者 A 來說， 101 大樓中間點及南、北方兩點之表面速度如圖四左所示；圖四中則為觀察者 B 所看到的：整個台北（地球表面）在圍他逆時針方向旋轉。

住在地球上的我們當然是隨著台北地球表面旋轉的觀察者 C：整個台北不轉不動，B 在順時針方向旋轉；如果 B 是「傅科擺」（記得掛它的條件嗎？），則是鐘擺平面在順時針方向旋轉！同樣的原理我們可以推論到：「傅科擺面」在北極會順時針方向旋轉（週期 24 小時）；在赤道上不旋轉（因南、北方兩點之速度一樣）；越北的「傅科擺」週期越短（因南、北方兩點之速度差別越大，註 5）。

結論

在「加速度運動」一節裡，我們談到了地球的自轉及公轉所產生的效應在日常物體的運動中，因與其它力相比太小了，很難偵測到。但在長距離和長時間的大規模運動中（如大氣中之空氣或海洋中之水），它還是可能脫穎而出變得很明顯的，例如海邊高（低）潮之所以每天出現兩次，正是因為地球自轉的關係（註 2）。

又如時常發生在台灣之熱帶氣旋（颶風）的形成，事實上也正是因地球自轉之故：在北半球產生逆時針的氣旋（註四），在南半球將產生順時針的氣旋。但赤道附近因旋轉太小，不會有颱風的。

除傅科擺外，要證明地球在動的原理似乎都很容易理解，但不容易執行；反之，傅科擺似乎容易製作，卻不容易理解。怪不得雖然早有人懷疑地球在動，但卻必須等了兩千年才能觀測到。即使在科技突飛猛進的今天，要證明地球在動似乎也不是幾個字就可以解釋清楚的，怪不得國中生（甚至大學生）只能支吾以對了。

*************** 猜猜看：旁觀者 A 是誰 ***************

我們在圖四及文中提到了「一位靜止不動的旁觀者 A」；不知讀者是否曾在心中質問「他是誰呢？」牛頓也曾想過這個問題：這位靜止不動的旁觀者在他心中是「絕對空間」——一個永遠存在那裡靜止不動的宇宙背景。

但是與他同時代的德國哲學家、科學家和數學家萊布尼茲（Gottfried Leibniz，1646 -1716）卻認為根本沒有這種空間，空間只是一種幻覺。對愛因斯坦發展廣義相對論有巨大啟發的馬赫（Ernst Mach，1838 -1916，奧地利物理學家兼哲學家）是一位十足的實證派人物，他認為任何可觀察到的現象都是相對於遙遠的恆星（或宇宙中所有的物體），因此從這裡得出地球在旋轉的結論是不合理的：我們怎麼知道不是恆星在旋轉呢？當太空沒有任何物體時，地球是否還在自轉呢？

德國哲學家、科學家兼數學家，萊布尼茲（Gottfried Leibniz，1646 -1716）　圖／wikimedia

奧地利物理學家與哲學家，馬赫（Ernst Mach，1838 -1916）　圖／wikimedia

他認為如果沒有其它物體比較，地球與靜止無異，旋轉沒有任何意義。因此對馬赫來說，加速不是絕對的、也是相對的！所以地球的自旋是相對於這「一位靜止不動的旁觀者」（遙遠的恆星）而言的，是它造成的！讀者相信馬赫的觀點嗎？或者根本沒有這個人（萊布尼茲幻覺空間）？或者還是比較相信牛頓的絕對空間？ ⋯⋯甚或是因為我去看它，所以地球才在旋轉的近代量子物理觀？對這些爭論有興趣的讀者請參考《我愛科學》。

註解

原來之擺錘在 2010 年 4 月 6 日因電纜斷裂損壞無法修復，現在的鉛擺為複製品。
伽利略錯誤地認為這一快一慢的（地球）速度變化正是造成潮汐現象的原因；依照他這一個理論，海邊高（低）潮每天只出現一次，但事實上我們知道因為地球自轉的關係，高（低）潮每天出現兩次。牛頓正確地解釋了潮汐現象主要是因月球引力造成的。
如果 B 或 C 向前丟出去一顆石子，則 B 將看到該石子直線前進；但是因為「科氏力」（Coriolis force ）的關係，C 將看到該顆石子沿右彎的曲線前進；詳見『「離心力」真的存在嗎？』。所以「科氏力」可用來解釋「傅科擺」在地球表面的軌跡（與地點緯度、從什麼地方啟動鐘擺、及鐘擺長度有關；加上鍾擺頂點雖然不隨地面旋轉，但並不是「絕對」靜止不動，而是隨地球自轉及公轉，因此細節上是很複雜的，以至於在網路上可以看到許多不同或不完全正確的軌跡圖）。
因為註 3 之「科氏力」。在網絡上可以看到不少用同樣的原理來解釋水槽、浴缸、或抽水馬桶排水時，在北半球的水流將是逆時針方向旋轉。筆者家中兩個抽水馬桶排水時都是逆時針旋轉，不知讀者府上是否也是一樣？但筆者覺得像加速度一樣，我們不可能偵測到地球自轉對這麼小之水體影響的，有興趣的讀者可參考英文《科學美國人》 2001 年的『有人終於以解決了「水流下排水管的方向是否會因您所在的半球而異」這個爭論？如果有，為什麼？』。
我們可以利用微積分來計算圖四中之旋轉速度。如果地球的半徑為 R，該中心點是地球表面緯度 Φ 上的一點，則其地球旋轉半徑應該是 Rcos(Φ)，將它乘以地球自轉速率 ė，即得在該點的直線速度。其上下兩點的直線速度微差 dėRcos(Φ) 造成對該點的旋轉（圖四中），將它除以旋轉微半徑 RdΦ 則得附近表面對該點的旋轉速率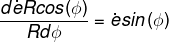：。鐘擺的週期與之成反比；台北的緯度為 25°N，故「傅科擺」的週期為 56.8小時[=(24小時)/sin (25°)]。