知乎精选 | 如何从零开始学习凸优化？

本文仅作为学术分享，如有侵权作删文处理

1：会打字的猿的回答

链接：

https://www.zhihu.com/question/68418633/answer/3178197426

我觉得Boyd这种大部头真心没必要看，当个工具书都嫌它啰嗦。花上一个月的时间看看比较好的讲义或者monograph完全足够打个基础了，剩下的根据想要做的具体方向看论文就好了。

推荐几个：

Bubeck的monograph: https://arxiv.org/abs/1405.4980 简洁明了，讲的东西不算很多（没有duality，ipm之类的）但是如果就入个门够用了。

Yin Tat Lee（这位绝对是tcs的巨星了）的课：https://yintat.com/teaching/cse535-spring21/  内容比Bubeck的丰富点儿，而且有不少比较前瞻性的讨论，但是不知道为啥找不到原先的讲义了，我记得曾经的版本里他还大致讨论了一下他和Sidford的技惊四座的path findingipm

Gärtner, Jaggi, Niao的讲义：https://github.com/epfml/OptML_course 这个是ETH和EPFL的孪生课程，和ML之类的更贴近一些

巨神Nesterov的https://link.springer.com/book/10.1007/978-1-4419-8853-9 这个稍微难一点儿，不过毕竟是Nesterov 的经典材料，也放在这里推荐吧

———————————————

另外我私心推荐一个稍稍偏题的：Vishnoi 的https://convex-optimization.github.io 这本书和其他几本不同在于它关注的是使用凸优化的手段求解离散优化问题，不夸张的讲，我个人认为最近十年凸优化真正重大的突破很重要的一部分都是从离散优化问题（尤其是网络流问题）推动的，最典型的就是YT Lee和Sidford的path finding ipm，连Lee都说他研究ipm的主要目的是搞网络流问题。其他的像box-simplex game，packing/cover LP的coordinate descent等等都是很精妙的东西。所以个人觉得Vishnoi这个视角很值得一看。

2：Martin Tan的回答

链接：

https://www.zhihu.com/question/68418633/answer/264232350

Boyd的书是本好书，但针对题目学习的目的，我强烈建议题主暂时不要学Boyd的Convex Optimization，理由如下：

1.  Boyd的书侧重凸分析的基础，花了非常长的篇幅介绍函数的凸性、对偶等，但在机器学习中，至少在刚入门不久的阶段这些东西用的不算多，或者说在大多数情况下只需要对这些有基本概念就行；

2. 这本书虽然很厚，但介绍的算法非常有限，学了很长时间你会觉得对你的研究基本毫无帮助，你要的东西书中没有，学的东西大多也用不上，让你很容易半途而废；

3.  目前机器学习领域优化研究的热点在往非凸优化转，ICML/NIPS上现在有越来越多的paper在研究算法在非凸情况下的收敛性（谁叫目前最热门的DNN是非凸的呢）。

我建议题目先读两个monograph：一个是Bubeck的《Convex Optimization: Algorithms and Complexity》，接下来再读Bottou、Curtis和Nocedal合作写的《Optimization Methods for Large-Scale Machine Learning》。前者从凸性的基本概念开始介绍，把常用的一阶算法都做了系统的介绍，它不需要任何优化基础就可以读懂；后者介绍了机器学习和优化交叉领域目前最新的研究成果，这个survey非常新，去年才写出来，今年也做过更新，而且作者也很牛，

Bottou是在机器学习和优化交叉方向最优秀的几位研究者之一，Nocedal是鼎鼎大名的传统优化大牛（目前在世的人中排前5应该不过分）。认真读过这两个过后，我相信题主看目前主流机器学习优化相关的paper、做一些相关研究毫无问题。

当然，如果题目想做好的研究，系统地学习凸优化的东西还是有必要的。这个可以等你入门了再一边做研究一边慢慢细读Convex Optimization、Numerical Optimization、Introductory Lectures on Convex Optimization等书。

本人也是做这方面研究的。我所在的组是做纯优化的，但我的研究方向更多偏向机器学习中的优化，paper也都发在NIPS等机器学习相关的会议上。所以我两边都比较了解，以上是以我自身体会给题主的建议。

3：齐思故齐在的回答

链接：

https://www.zhihu.com/question/68418633/answer/2267537558

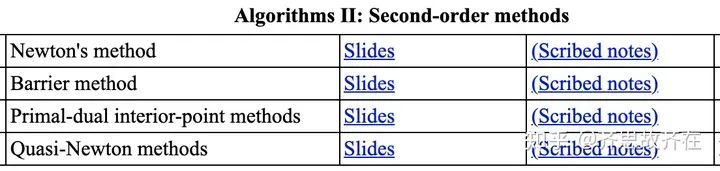
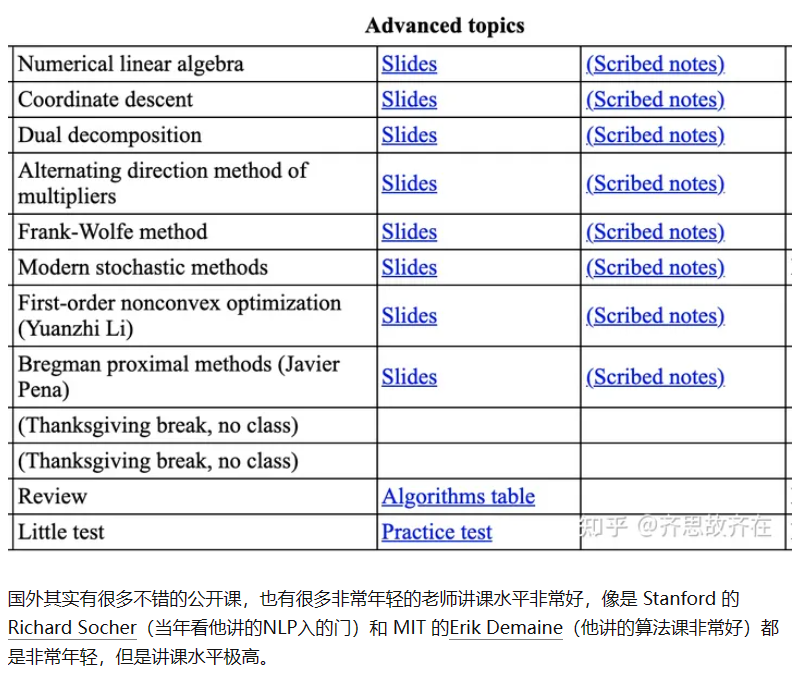
微信公众号后台回复

加群：加入全球华人OR|AI|DS社区硕博微信学术群

资料：免费获得大量运筹学相关学习资料

人才库：加入运筹精英人才库，获得独家职位推荐

电子书：免费获取平台小编独家创作的优化理论、运筹实践和数据科学电子书，持续更新中ing…

加入我们：加入「运筹OR帷幄」，参与内容创作平台运营

知识星球：加入「运筹OR帷幄」数据算法社区，免费参与每周「领读计划」、「行业inTalk」、「OR会客厅」等直播活动，与数百位签约大V进行在线交流

文章须知

文章作者：会打字的猿、Martin Tan、齐思故齐在等

责任编辑：疑疑

微信编辑：疑疑

文章由『运筹OR帷幄』转载发布

如需转载请在公众号后台获取转载须知

关注我们 

       FOLLOW US