人工智能的各个领域,包括自然语言处理、计算机视觉、语音处理,借助深度学习的强大威力,都取得了令人叹为观止的巨大进步。将深度学习技术应用于传统的科学领域,如物理、化学、生物、医学,即所谓的 AI for Science(科学智能),作为一个新的交叉学科,也逐渐兴起,孕育着巨大的潜力,受到广泛的关注。
ByteDance Research 也在进行 AI for Science 的研究,包括机器学习与量子化学、大规模量子化学计算、AI 制药等领域一些问题的研究,希望跟业界一起推动领域的发展。本文简要介绍我们这两年来取得的一些进展。也抛砖引玉,希望与业界进行更多的交流和合作。
在机器学习和量子化学方向,我们提出的 LapNet 算法,比有代表性的 FermiNet 模型训练速度提高了 10 倍,能计算的化学体系的规模和精度目前是领域最大的。
在大规模量子化学计算方向,我们开发了 Periodic DMET 算法,使用经典和量子混合计算机(实际是在经典计算机上的模拟),用于周期性体系的计算,只用 20 个量子比特就达到了之前方法用近万个量子比特才能达到的精度。
在 AI 制药方向,我们开发的 LM-Design 模型,利用大量蛋白质序列数据,以及一定数量的蛋白质结构和序列对应数据,学习从蛋白质结构到序列转换的模型,达到了目前蛋白质序列设计的最高精度。
机器学习与量子化学
物理学家狄拉克曾说:对大部分物理学和整个化学,进行数学建模所需要的基本定律已完全清楚,困难只在于这些定律的应用,得到的方程一般都太复杂而无法求解。
量子化学是根据量子力学的原理研究化学现象的学科。其重要的问题是用计算的方法求解分子或周期性体系(如固体)的电子薛定谔方程,从而推算出分子或周期性体系的基态能量、电极性等特性。是所谓的从头计算(ab initio)问题。传统的方法有密度泛函理论 DFT、耦合簇 CCSD 等。要么计算的精度不够高,要么能计算的规模不够大。
近年,用机器学习的方法解决从头计算问题成为倍受关注的新方向。其基本想法是借助深度学习强大的表示和学习能力,大幅提升从头计算的精度和规模。其中的一个路径是 NN-VMC(Neural Network based Variational Monte Carlo) 。用神经网络近似薛定谔方程的波函数,通过随机采样的方式获得体系中电子在空间中的样本,这样可以计算基于薛定谔方程的整个体系的能量。通过最小化能量的上界,优化神经网络的参数,不断迭代,最后得到近似最优的神经网络(波函数),以及体系的近似基态能量(最小能量)。(注:波函数的平方是电子在空间出现的概率密度函数,有了波函数,就可以进行电子在空间中的随机采样。)图 1 显示 NN-VMC 的基本原理。其核心问题是如何设计神经网络和学习算法。
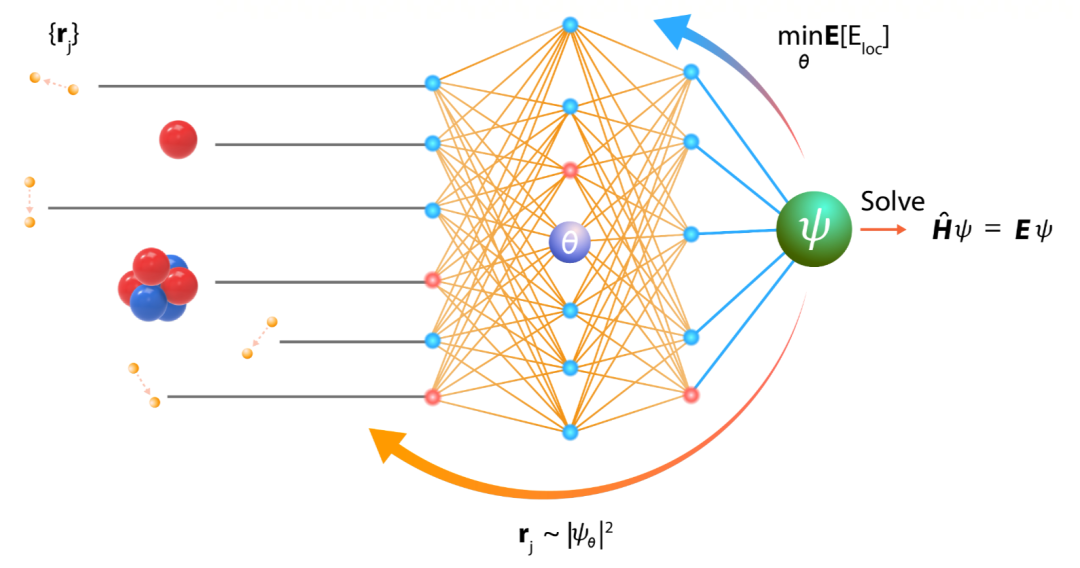
图 1. NN-VMC 方法的基本原理
NN-VMC 中有代表性的方法是 DeepMind 和 ICL 于 2019 年提出的 FermiNet。之后一些研究机构又提出了一些新的方法。ByteDance Research 从 2021 年起,与北京大学合作,进行了一系列相关研究,提出了几个新的方法。下面对这些方法做一简单介绍。
NN-VMC+ECP,是我们开发的结合 NN-VMC 和赝势 ECP(Effective Core Potential)的方法 [1],可以进一步提高计算的效率和体系的规模。计算化学体系的特性时,往往只需要关注原子中外侧轨道的电子。将原子中内侧轨道的电子的势能用定量表示,就可以大幅减少所需要的计算量。我们将 ECP 技巧应用于 NN-VMC,得到了这个新方法,取得了很好的效果。
NN-DMC,是我们提出的将神经网络和扩散蒙特卡洛法 DMC(Diffusoon Monte Carlo)结合的另一个方法 [2]。DMC 与 VMC 不同,不是计算体系基态能量的上界,而是使用虚时演化来计算体系的基态能量。这个方法,相比 FermiNet 等已有方法也能大幅提高计算的精度和规模。
最近开发的 LapNet 也是一种 NN-VMC 方法 [3],特点是在神经网络学习时使用前向拉普拉斯算子( Forward Laplacian)。基于薛定谔方程计算体系的能量上界的过程中,需要计算哈密顿算子,包括其中的动能部分。之前的方法都是通过计算相关的黑塞矩阵的方式计算动能,其算法复杂度高,成为学习的一个瓶颈。LapNet 在学习的前向传播中,通过拉普拉斯算子的计算,直接计算动能,以及哈密顿算子,从而省去了黑塞矩阵的计算。这样可以大幅提高学习的计算效率。相比 FermiNet,LapNet 有平均 10 倍左右的加速。
ECP、DMC 和 Forward Laplace 属于三种不同的技术改进(简化势能计算、优化采样,提高计算效率),三个技术结合起来原理上可以更大程度上提高计算规模,也是我们正在尝试的方法。另外,我们还将 NN-VMC 方法应用于固体的薛定谔方程求解 [4],分子体系的力场 [5]、电极化计算 [6] 等问题,证明了 NN-VMC 方法的实用性。
图 2 显示目前 NN-VMC 方法中代表性工作的精度和规模,纵轴表示精度,圆的大小表示规模。我们提出的 LapNet 方法能够以更高的精度计算更大的体系。最大的体系有 116 个电子。
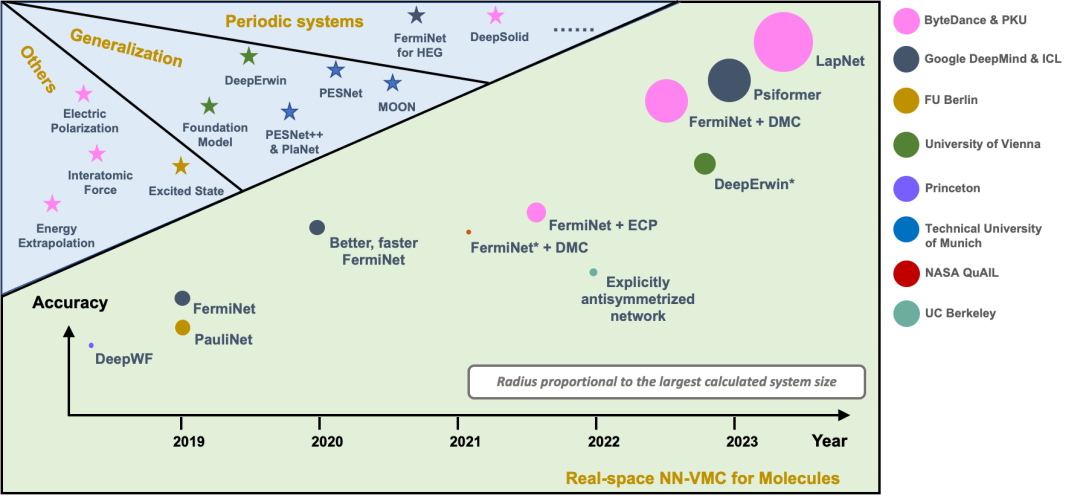
图 2. NN-VMC 方法的规模和精度
大规模量子化学计算
通过直接求解薛定谔方程计算化学体系特性(比如基态能量)的方法能处理的规模仍然有限。量子嵌入方法(Quantum Embedding Method)被认为是解决这个问题的一条有效路径。基本想法是通过分而治之和多精度计算实现大规模化。代表性的方法有密度矩阵嵌入理论 DMET(Density Matrix Embedding Theory)。将体系划分为若干部分(Fragment),对其中的每个 Fragment 及其对应的环境(Bath)进行高精度计算,对其他部分进行低精度计算。而且根据需要对每个 Fragment 进行并行处理。最后再把高精度计算的结果合并起来,不断迭代逼近原始体系。这样可以大幅提高可计算的体系的规模。
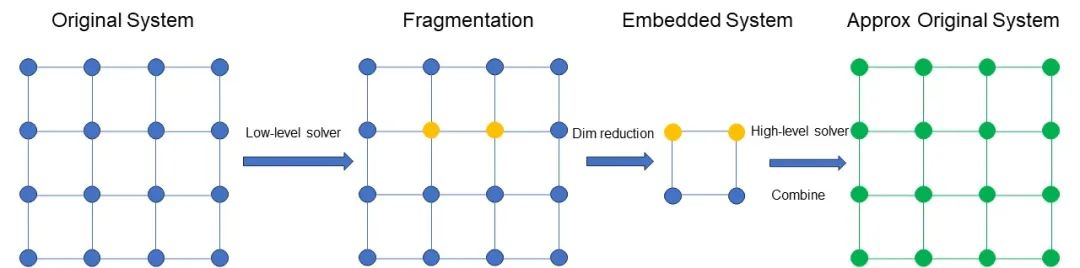
图 3 DMET 方法的直观解释
图 3 示意 DMET 方法的过程。首先对原始体系进行划分,得到一组 Fragment。假设图中黄色部分是我们关注的 Fragment,例如是两个原子。图中蓝色的部分包含环境和其他部分。对关注的 Fragment 及其环境用高精度的方法计算,例如 CCSD,对其他部分用低精度的方法计算,例如,Hartree–Fock 法。对所有的 Fragment 做同样的并行处理。
具体算法如下。首先,通过低精度求解,得到整体(关注的 Fragment、环境和其他部分)的约化密度矩阵,这个低精度解包含参数。其次,对这个矩阵的 Fragment 及其环境进行奇异值分解,构建投影算符 P(该投影算符仅关注 Fragment 及其环境),利用投影算符构建低维度的体系(图片),并对其进行高精度求解。之后,将所有 Fragment 的计算结果合并,作为体系整体的近似。最后,通过迭代,调节参数,使得原始的低精度解逐渐逼近合并的高精度解(在 L2 norm 的意义下),直到得到最终结果。
我们基于两种完全不同的计算范式,实现 DMET 及其变种的 SIE,进行大规模量子化学体系的计算。一是使用经典计算机,另一个是使用量子计算机。本文主要介绍后者的相关工作(前者的工作计划今后有更大进展时介绍),也称为量子计算化学。我们考虑在量子计算机上的实现,但只在经典计算机上进行模拟,希望为量子化学的发展做出贡献。无论是哪种计算范式,DMET 方法使得大规模计算成为可能,我们正在尝试努力实现 DMET,将可计算的体系提升几个数量级。
物理学家费曼曾说:自然不是古典力学,如果你想模拟自然,你最好用量子力学。开发量子计算技术的驱动力就是用量子层面的计算设备模拟量子现象。换言之,量子化学是量子计算最合适的应用领域之一。
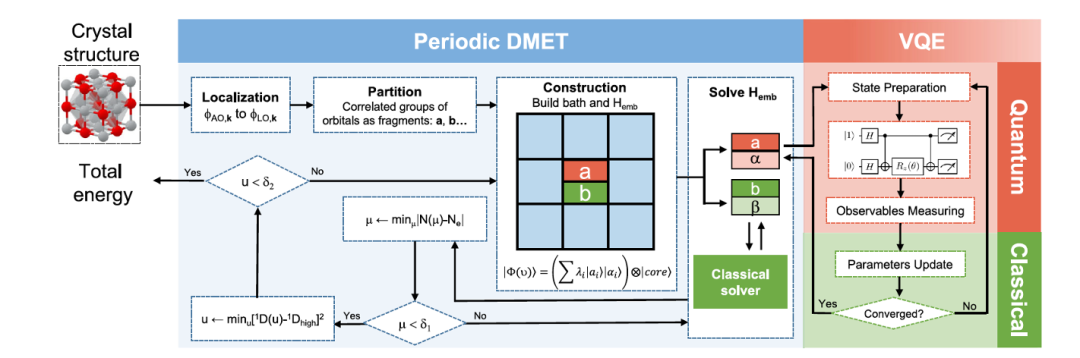
图 4. Periodic DMET 方法的示意
我们先后开发了两个量子计算化学方法,结合量子和经典混合计算机和 DMET 的特点,大幅提高了计算体系的精度和规模。基本想法是用量子计算机实现 DMET 高精度计算的部分,用经典计算机实现 DMET 低精度计算的部分。DMET-ESVQE 计算分子体系 [7], Periodic DMET 计算周期性体系 [8]。前者只用 16 个量子比特,就能实现之前的方法用 144 个量子比特的计算。后者只用 20 个量子比特就能实现之前的方法用将近 1 万个量子比特的计算。
图 4 显示在混合计算机上实现的 DMET Periodic 方法。输入是晶体,输出是体系的能量。首先对体系进行划分,然后并行地计算每一个 Fragment。对关注 Fragment 及其环境在量子计算机上用 U-CCSD 求解。对其他部分在经典计算机上用 Hartree–Fock 法求解。
量子蒙特卡罗法,包括 VMC、DMC,是量子化学的最有效的一系列算法 [9]。我们还提出了将量子计算和量子蒙特卡罗法结合的新方法。这个方法可以体现量子计算对量子化学的一些优势。具体地,量子计算可以部分解决量子蒙特卡洛法中的符号问题。
AI 制药
使用 AI 技术辅助药物发现已经成为被业界广为接受的新范式。近年有大量的研究,也有一些技术应用于实际的场景。我们进行了基于 AI 技术的药物设计的研究和开发,包括小分子药物和大分子药物(抗体药物)。
小分子药物设计过程包括蛋白质靶点的发现,小分子药物候选的生成,候选与靶点(target)的亲和性、候选的成药性、无毒性等的判断。目前有 AI 技术可以实现这些药物的开发步骤。我们开发了基于机器学习的小分子药物候选生成的方法,MARS 是利用打分函数自动生成候选的方法 [10],DESERT 是根据靶点的形状自动生成候选的方法 [11]。
MARS 从种子分子开始,不断编辑分子,直到最后得到最优的小分子药物候选。生成的过程中使用马尔可夫链蒙特卡洛法(MCMC),其平稳分布是由多个打分函数构成的概率分布。打分函数表示小分子药物候选的亲和性、成药性、无毒性等。建议分布表示基于图神经网络(MPNN)进行小分子药物候选的编辑前后的条件概率分布。图神经网络表示小分子化合物的分子式,结点是原子,边是化学键。对小分子的编辑包括增加新的结点和删除已有的结点。图神经网络上可以预测对小分子的可能的编辑操作(增加或删除),其参数通过学习得到。MARS 只需要有打分函数、小分子药物的数据库(分子式)就可以生成全新的和多样的小分子药物候选。目前 MARS 已经被用于实际的小分子药物设计工作中。
DESERT 通过两个步骤进行小分子药物候选的生成。Sketching:采样与蛋白质靶点的口袋(pocket)形状互补的药物候选的形状,Generating:基于药物候选的形状自动生成药物候选的分子式。图 5 显示这个过程。
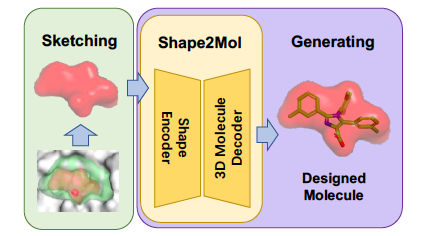
图 5. DESERT:自动生成小分子药物候选
候选和靶点结合,其必要条件是两者的形状能够进行很好的对接。在 Sketching 阶段,根据蛋白质靶点的形状,用启发式的方法产生候选的形状。在 Generating 阶段,用事先学好的形状到分子的生成模型 Shape2Mol 根据形状自动生成分子式。可以利用分子库里的大量的药物的分子式和形状,学习这个生成模型。如图 6 所示,Shape2Mol 中,编码器将分子 3D 形状进行编码,产生中间表示,解码器根据中间表示生成分子式。3D 形状使用体素表示,分子式使用符号序列表示。DESERT 是 2022 年小分子药物候选生成结合性能最好的方法。
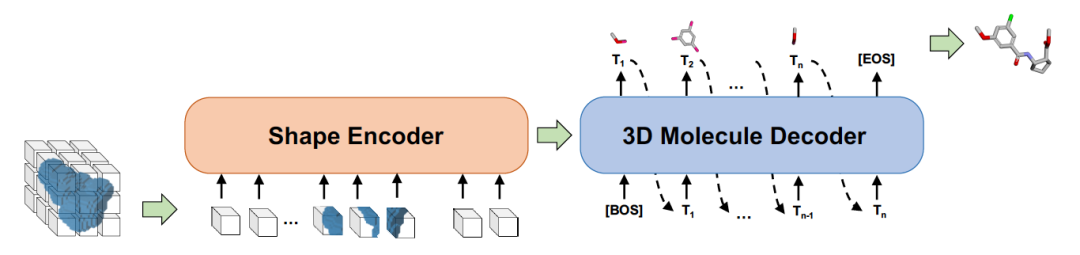
图 6. 形状到分子的生成模型 Shape2Mol 的示意
最近我们聚焦在大分子药物设计上,更一般的问题是蛋白质设计。蛋白质设计包括抗体药物设计,多肽药物设计等。如果知道了蛋白质序列(氨基酸序列),就可以预测其结构,知道了蛋白质结构也就能预测其功能。这就是著名的 AlphaFold 做的事情。蛋白质设计可以看作是一个反向的过程。一般从功能出发决定对应的蛋白质结构,再根据蛋白质结构决定对应的蛋白质序列。我们开发了从蛋白质结构生成蛋白质序列的模型 LM-Design。
LM-Design 的输入是蛋白质结构,输出是对应的蛋白质序列。LM-Design 由结构编码器和序列解码器组成。其中,结构编码器是已训练好的表示蛋白质结构的图神经网络;序列解码器基于已预训练好的大规模蛋白质语言模型(Protein Language Model),与 BERT/Transformer Encoder 相似(使用双向自注意力),在最后一层插入一个结构适配器(Structural Adaptor)。结构适配器的参数是待学习的。图 7 给出 LM-Design 的模型架构。
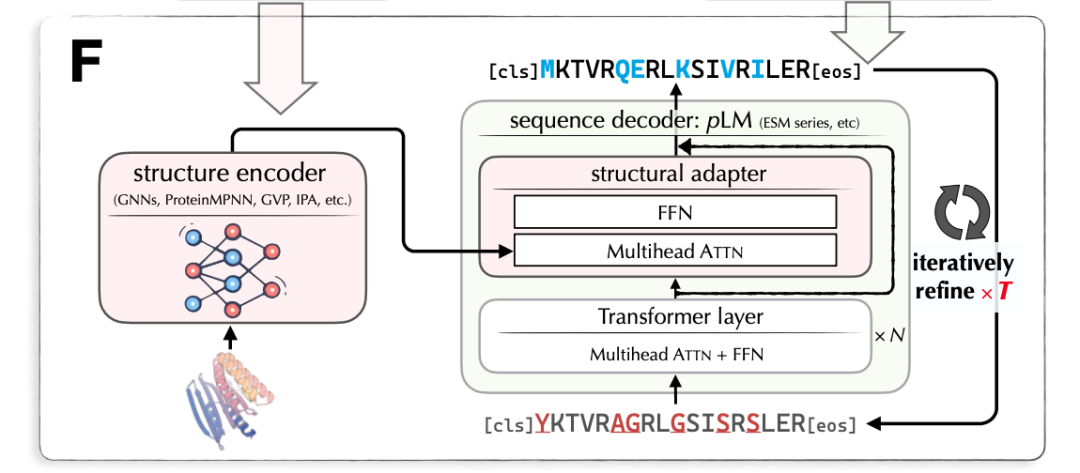
图 7. 蛋白质结构到序列的生成模型 LM-Design 的架构
LM-Design 的学习和预测是掩码语言建模(Masked Language Modeling),与 BERT 模型的训练相似,其目标是多次还原被掩码的序列中的符号(氨基酸)。也就是说,基于已训练好的蛋白质语言模型中的信息,以及当前的蛋白质结构信息,对蛋白质序列进行多次改写。LM-Design 基于全局序列信息对其中很少一部分符号(氨基酸)进行改写,所以对蛋白质远距离依存关系能够进行很好的表示和预测。注:蛋白质折叠之后,序列上距离很远的氨基酸在结构上也可能很近。
现实中有大量经过测序的蛋白质序列数据,但只有少量的蛋白质结构与序列对齐的数据。LM-Design 的一个优势是可以利用海量的蛋白质序列数据,充分学习和利用蛋白质序列之间的进化中产生的关联关系,大幅提高从蛋白质结构到序列生成的预测准确率。此外,我们发现增大预训练蛋白质模型的规模可以进一步提升准确率。如图 8 所示,LM-Design 是目前效果最好的蛋白质序列生成模型,图中圆的大小表示模型的参数量。

图 8. 蛋白质序列生成方法的精度
致谢
感谢任维络、吕定顺、顾全全、吴凯、郑在翔、周奕、罗曼平、张震宇为本文撰写提供的建议和帮助。
参考文献
[1] Xiang Li, Cunwei Fan, Weiluo Ren, and Ji Chen. Fermionic neural network with effective core potential. Phys. Rev. Research 2022.
[2] Ren, W., Fu, W., Wu, X. et al. Towards the ground state of molecules via diffusion Monte Carlo on neural networks. Nature Communication 14, 2023.
[3] Ruichen Li, Haotian Ye, Du Jiang, Xuelan Wen, Chuwei Wang, Zhe Li, Xiang Li, Di He, Ji Chen, Weiluo Ren, Liwei Wang. Forward Laplacian: A New Computational Framework for Neural Network-based Variational Monte Carlo. 2023.
[4] Li, X., Li, Z. & Chen, J. Ab initio calculation of real solids via neural network ansatz. Nature Communications 13, 2022.
[5] Yubing Qian, Weizhong Fu, Weiluo Ren, Ji Chen. Interatomic force from neural network based variational quantum Monte Carlo. Journal Chemical Physics. 157, 2022.
[6] Xiang Li, Yubing Qian, Ji Chen. Electric Polarization from Many-Body Neural Network Ansatz, 2023.
[7] Li, W., Huang, Z., Cao, C., Huang, Y., Shuai, Z., Sun, X., … & Lv, D. (2022). Toward practical quantum embedding simulation of realistic chemical systems on near-term quantum computers. Chemical science, 13 (31), 8953-8962.
[8] Cao, C., Sun, J., Yuan, X., Hu, H. S., Pham, H. Q., & Lv, D. (2023). Ab initio quantum simulation of strongly correlated materials with quantum embedding. NPJ Computational Materials, 9 (1), 78.
[9] Zhang, Y., Huang, Y., Sun, J., Lv, D. and Yuan, X., 2022. Quantum computing quantum monte carlo. arXiv preprint arXiv:2206.10431.
[10] Xie, Y., Shi, C., Zhou, H., Yang, Y., Zhang, W., Yu, Y. and Li, L., MARS: Markov Molecular Sampling for Multi-objective Drug Discovery, ICLR 2021.
[11] Long, S., Zhou, Y., Dai, X. and Zhou, H., 2022. Zero-shot 3d drug design by sketching and generating. Advances in Neural Information Processing Systems, 35, pp.23894-23907.
[12] Zheng, Z., Deng, Y., Xue, D., Zhou, Y., Ye, F. and Gu, Q. Structure-informed language models are protein designers. ICML 2023.



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


