【运动学】基于CV、CA、CT三种运动模型轨迹附Matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法       神经网络预测       雷达通信      无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

❤️ 内容介绍

在运动学中，我们经常使用不同的运动模型来描述物体的运动轨迹。在计算机视觉领域，CV（常速度）、CA（常加速度）和CT（常转弯率）是三种常见的运动模型。本文将详细介绍这三种模型，并讨论它们在轨迹预测和目标跟踪中的应用。

1. CV模型（Constant Velocity）

CV模型假设物体在运动过程中保持恒定的速度。这意味着物体的位置随时间线性变化。CV模型的数学表示如下：

x(t) = x(0) + v*t

其中，x(t)是物体在时间t时刻的位置，x(0)是初始位置，v是恒定的速度。

CV模型的优点是简单且易于实现。它适用于描述匀速直线运动的物体，如行人、车辆等。然而，CV模型无法捕捉到加速度和转弯的变化，因此在某些情况下可能不够准确。

1. CA模型（Constant Acceleration）

CA模型假设物体在运动过程中保持恒定的加速度。这意味着物体的速度随时间线性变化，位置随时间二次变化。CA模型的数学表示如下：

x(t) = x(0) + v*t + (1/2)at^2

其中，a是恒定的加速度。

CA模型比CV模型更加复杂，但也更加准确。它适用于描述加速度变化的物体，如运动车辆、飞机等。CA模型可以预测物体的位置和速度，并提供更准确的轨迹预测。

1. CT模型（Constant Turn Rate）

CT模型假设物体在运动过程中保持恒定的转弯率。这意味着物体的转向角速度随时间恒定，位置和速度随时间非线性变化。CT模型的数学表示如下：

x(t) = x(0) + v*(sin(ψ(t)) – sin(ψ(0)))/ω

y(t) = y(0) – v*(cos(ψ(t)) – cos(ψ(0)))/ω

其中，(x(t), y(t))是物体在时间t时刻的位置，(x(0), y(0))是初始位置，v是恒定的速度，ψ(t)是物体在时间t时刻的转向角度，ψ(0)是初始转向角度，ω是恒定的转弯率。

CT模型是描述弯道运动的理想选择，如飞机的曲线飞行或车辆的弯道行驶。它可以更准确地预测物体的位置和速度，并提供更真实的轨迹模拟。

在计算机视觉中，CV、CA和CT模型在目标跟踪和轨迹预测中发挥着重要的作用。根据物体的运动特征和场景需求，选择合适的模型可以提高跟踪和预测的准确性。

总结起来，CV模型适用于描述匀速直线运动，CA模型适用于描述加速度变化，CT模型适用于描述弯道运动。了解这三种运动模型的特点和应用场景，有助于我们更好地理解和应用运动学原理，提高计算机视觉领域的相关技术。

🔥核心代码

% 跟踪函数function data = simutrack_cv(x0, y0, z0, v0, theta, phi, sigma_ax, sigma_ay, sigma_az, sigma_r, sigma_theta, sigma_phi, sigma_v, T, N)%simutrack 仿真带加速度扰动的匀速直线运动目标的二维航迹.%% 'x0' 目标在x方向上的初始位置% 'y0' 目标在y方向上的初始位置% 'z0' 目标在z方向上的初始位置% 'v0' 目标运动方向上的初始速度% 'theta' 目标初始运动方向与x轴的夹角% 'phi' 目标初始运动方向与xy平面的夹角% 'sigma_ax' x轴方向的随机加速度(过程噪声)% 'sigma_ay' y轴方向的随机加速度(过程噪声)% 'sigma_az' z轴方向的随机加速度(过程噪声)% 'sigma_r' 极坐标下距离的测量标准差% 'sigma_theta' 极坐标下方位的测量标准差，单位度% 'sigma_phi' 极坐标下俯仰的测量标准差，单位度% 'sigma_v' 极坐标下径向速度的测量标准差% 'T' 雷达扫描周期% 'N' 采样点数% 'data' 仿真得到的N点目标航迹[斜距 方位角 俯仰角 径向速度] % 角度转变为弧度theta = theta*pi/180;phi=phi*pi/180; % xyz方向上的初始速度vx0 = v0 * cos(theta)*cos(phi);vy0 = v0 * sin(theta)*cos(phi);vz0 = v0 * sin(phi);
% 状态转移矩阵F = [1 T 0 0 0 0; 0 1 0 0 0 0; 0 0 1 T 0 0 ; 0 0 0 1 0 0;0 0 0 0 1 T;0 0 0 0 0 1];
% 过程噪声分布矩阵Tao = [T^2/2 0 0;T 0 0;0 T^2/2 0 ; 0 T 0;0 0 T^2/2;0 0 T];
% 测量矩阵% H = [1 0 0 0 0 0;0 0 1 0 0 0;0 0 0 0 0 1 ]; % 构造真实航迹X(:,1) = [x0 vx0 y0 vy0 z0 vz0]';for m = 2:N X(:,m) = F*X(:,m-1)+Tao*[sigma_ax*randn(1) sigma_ay*randn(1) sigma_az*randn(1)]'; %N个点迹的坐标end % 极坐标下的数值r0 = sqrt(X(1,:).^2+X(3,:).^2+X(5,:).^2); %斜距theta0 = atan(X(3,:)./X(1,:))*180/pi; %方位角phi0 = atan(X(5,:)./sqrt(X(1,:).^2+X(3,:).^2))*180/pi; %俯仰角vr0 = -(X(1,:).*X(2,:)+X(3,:).*X(4,:)+X(5,:).*X(6,:))./r0; %径向速度
for i=1:N if(X(1,i)>=0&&X(3,i)>0) theta0(i)=theta0(i); else if(X(1,i)>=0&&X(3,i)<0) theta0(i)=theta0(i)+360; else theta0(i)=theta0(i)+180; end endend
% 加高斯观测噪声 r = r0 + sigma_r*randn(1,N); theta = theta0 + sigma_theta*randn(1,N); phi = phi0+sigma_phi*randn(1,N);vr = vr0+sigma_v*randn(1,N);
data = [r', theta',phi',vr'];







❤️ 运行结果

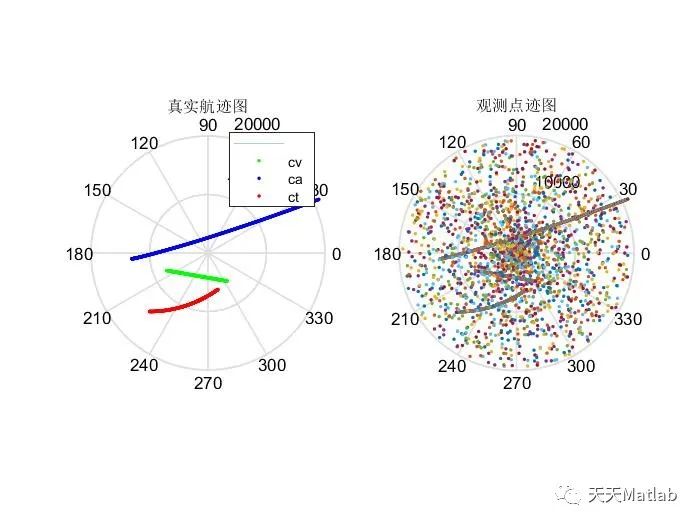
⛄ 参考文献

[1] 王耀林、盖梦欧、周敏.IMM算法在空中复杂机动目标跟踪中的应用[J].现代信息科技, 2020, 4(13):3.DOI:CNKI:SUN:XDXK.0.2020-13-003.

[2] 刘成成.复杂环境下强机动目标跟踪算法研究[D].上海交通大学[2023-09-09].DOI:CNKI:CDMD:2.1015.806555.

[3] 潘雁鹏.基于时差量测的目标定位与跟踪算法研究[D].西安电子科技大学,2020.

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料

🍅 私信完整代码和数据获取及论文数模仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配

、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长 火灾扩散

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合、状态估计