✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
🔥 内容介绍
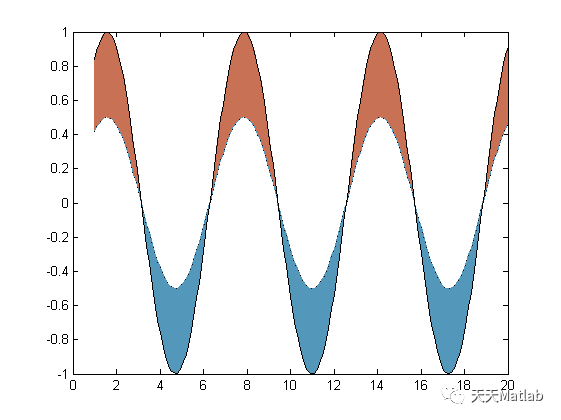
climanomaly plots two lines (y vs. x and y vs. ref) and visualisespositive and negative anomalies by shading the area between both lines intwo different colors. This is useful for visualising anomalies of a timeseries relative to a climatology. The function can further be used toplot anomalies relative to a constant baseline or two threshold baselines(positive anomaly above upper threshold, negative anomaly below lowerthreshold).
Syntax
climanomaly(x,y,ref) climanomaly(…,’top’,ColorSpec) climanomaly(…,’bottom’,ColorSpec) climanomaly(…,’mainline’,’LineSpec’) climanomaly(…,’refline’,’LineSpec’) [hlin,href,htop,hbot] = CLIMANOMALY(…)
Description
climanomaly(x,y,ref) plots a y vs. x (main line) and y vs. ref (referenceline) and shades areas line values above zero; blue fills the areabetween zero and any values below zero.
-
To shade anomalies relative to a variable reference (e.g. aclimatology) specify ref as a vector the length of y.
-
To shade anomalies relative to a constant baseline, specify a singleref value.
-
To shade anomalies relative to an upper and a lower threshold, specifytwo ref values (e.g., let ref be [-0.4 0.5] to shade all values lessthan 0.4 or greater than 0.5).
climanomaly(…,’top’,ColorSpec) specifies the top color shading, whichcan be described by RGB values or any of the Matlab short-hand colornames (e.g., ‘r’ or ‘red’).
climanomaly(…,’bottom’,ColorSpec) specifies the bottom shading color.
climanomaly(…,’mainline’,’LineSpec’)climanomaly(…,’refline’,’LineSpec’)Specifies line types, plot symbols and colors of the reference line.LineSpec is a string of characters, e.g. ‘b–*’. Refer to the ‘plot’documentation for more options. By default, the main line will be plottedas a solid black line (‘k-‘) and the reference line as a dotted blackline (‘k:’).
[hlin,href,htop,hbot] = climanomaly(…) returns the graphics handles ofthe main line, top, and bottom plots, respectively.
📣 部分代码
clcclear allclose allx = 1:.1:20;y = sin(x);ref = sin(x)/2;figureclimanomaly(x,y,ref);
function [hlin,href,htop,hbot] = climanomaly(x,y,ref,varargin) CLIMANOMALY plots two lines (y vs. x and y vs. ref) and visualises positive and negative anomalies by shading the area between both lines in two different colors. This is useful for visualising anomalies of a time series relative to a climatology. The function can further be used to plot anomalies relative to a constant baseline or two threshold baselines (positive anomaly above upper threshold, negative anomaly below lower threshold).% Syntax CLIMANOMALY(x,y,ref) CLIMANOMALY(...,'top',ColorSpec) CLIMANOMALY(...,'bottom',ColorSpec) CLIMANOMALY(...,'mainline','LineSpec') CLIMANOMALY(...,'refline','LineSpec') [hlin,href,htop,hbot] = CLIMANOMALY(...) % Description CLIMANOMALY(x,y,ref) plots a y vs. x (main line) and y vs. ref (reference line) and shades areas line values above zero; blue fills the area between zero and any values below zero. - To shade anomalies relative to a variable reference (e.g. a climatology) specify ref as a vector the length of y. - To shade anomalies relative to a constant baseline, specify a single ref value. - To shade anomalies relative to an upper and a lower threshold, specify two ref values (e.g., let ref be [-0.4 0.5] to shade all values less than 0.4 or greater than 0.5). CLIMANOMALY(...,'top',ColorSpec) specifies the top color shading, which can be described by RGB values or any of the Matlab short-hand color names (e.g., 'r' or 'red'). CLIMANOMALY(...,'bottom',ColorSpec) specifies the bottom shading color. CLIMANOMALY(...,'mainline','LineSpec') CLIMANOMALY(...,'refline','LineSpec') Specifies line types, plot symbols and colors of the reference line. LineSpec is a string of characters, e.g. 'b--*'. Refer to the 'plot' documentation for more options. Use 'none' to plot the anomalies without By default, the main line will be plotted as a solid black line ('k-') and the reference line as a dotted black line ('k:'). [hlin,href,htop,hbot] = CLIMANOMALY(...) returns the graphics handles of the main line, top, and bottom plots, respectively.% Examples Example 1: Simple plot% Example 2: Change line and patch appearance x = 1:.1:20; y = sin(x); ref = sin(x)/2; figure [hlin,href,htop,hbot] = CLIMANOMALY(x,y,ref,'top','k','bottom',[.9 .9 .9],... 'mainline','b-','refline','r--'); hlin.LineWidth = 2; href.LineWidth = 2; alpha(htop,0.7) alpha(hbot,0.7) % Author Info Jake Weis, University of Tasmania, Institute for Marine and Antarctic Studies (IMAS), April 2021 This function is based on the 'anomaly' function, written by Chad A. Greene (<a href="matlab:web('https://github.com/chadagreene/CDT')">Climate Data Toolbox</a>). Subfunction used: 'intersections' by Douglas M. Schwarz. See also: plot, boundedline, area, patch, and fill.%% Error checks:narginchk(3,inf)assert(numel(ref)<=2 | numel(ref)==numel(y),'Input error: The refold must either be one or two scalars or the length of y.')assert(numel(x)==numel(y),'Input error: The dimensions of x and y must agree.')assert(isvector(x),'Input error: x and y must be vectors of the same dimension.')assert(issorted(x),'Input error: x must be monotonically increasing.')%% Set defaults:% These are RGB values from cmocean's balance colormap (Thyng et al., 2016):topcolor = [0.7848 0.4453 0.3341];bottomcolor = [0.3267 0.5982 0.7311];% Reference line will be plotted by defaultmainspec = 'k-';refspec = 'k:';%% Input parsing:if nargin>3 % Top face color: itop = find(strncmpi(varargin,'topcolor',3),1); if ~isempty(itop) topcolor = varargin{itop+1}; varargin(itop:itop+1) = []; end % Bottom face color: ibot = find(strncmpi(varargin,'bottomcolor',3),1); if ~isempty(ibot) bottomcolor = varargin{ibot+1}; varargin(ibot:ibot+1) = []; end % Main and reference line properties: imai = find(strncmpi(varargin,'mainline',3),1); iref = find(strncmpi(varargin,'refline',3),1); if ~isempty(imai) mainspec = varargin{imai+1}; varargin(imai:imai+1) = []; end % Reference line: iref = find(strncmpi(varargin,'refline',3),1); if ~isempty(iref) refspec = varargin{iref+1}; varargin(iref:iref+1) = []; endend%% Data manipulation:% Convert ref into a top and a bottom column vector the length of yif numel(ref) == 1 reft = repmat(ref,numel(y),1); refb = repmat(ref,numel(y),1);elseif numel(ref) == 2 reft = repmat(max(ref),numel(y),1); refb = repmat(min(ref),numel(y),1);else reft = ref(:); refb = ref(:);end% Columnate inputs to ensure consistent behavior:x = x(:);y = double(y(:));% Archive the x and y values before tinkering with them (we'll plot the archived vals later).x_archive = x;y_archive = y;reft_archive = reft;refb_archive = refb;% If y contains nans, ignore them so filling will work:ind = (isfinite(y) & isfinite(reft) & isfinite(refb));x = x(ind);y = y(ind);reft = reft(ind);refb = refb(ind);% Find zero crossings so shading will meet the refline properly: First for the bottom:[xct,yct] = intersections(x,y,x,reft); % intersections is a subfunction by Douglas Schwarz, included below. Now for the top:[xcb,ycb] = intersections(x,y,x,refb); % intersections is a subfunction by Douglas Schwarz, included below.% Add zero crossings to the input dataset and sort them into the proper order:xb = [x;xcb];xt = [x;xct];yb = [y;ycb];yt = [y;yct];reft = [reft;yct];refb = [refb;ycb];[xb,ind] = sortrows(xb);yb = yb(ind); % sorts yb with xbrefb = refb(ind); % sorts refb with xb[xt,ind] = sortrows(xt);yt = yt(ind); % sorts yt with xtreft = reft(ind); % sorts reft with xt% Start thinking about this as two separate datasets which share refline values where they meet:refb) = refb(yb>refb);yt(yt<reft) = reft(yt<reft);%% Plot top and bottom y datasets using the area function:% Get initial hold state:hld = ishold;% Plot the top half:htop = fill([xt;flipud(xt)],[yt;flipud(reft)],topcolor,'LineStyle','none');hold on Plot the bottom half:hbot = fill([xb;flipud(xb)],[yb;flipud(refb)],bottomcolor,'LineStyle','none');if ~strcmp(mainspec,'none') % Plot the main line (the "archive" values are just the unmanipulated values the user entered) hlin = plot(x_archive,y_archive,mainspec);else hlin = cell(1,1);endif ~strcmp(refspec,'none') % Plot the main line (the "archive" values are just the unmanipulated values the user entered) href(1) = plot(x_archive,reft_archive,refspec); if numel(ref) == 2 % Plot the main line (the "archive" values are just the unmanipulated values the user entered) href(2) = plot(x_archive,refb_archive,refspec); endelse if numel(ref) ~= 2 href = cell(1,1); else href = cell(2,1); endend% Return the hold state if necessary:if ~hld hold offend%% Clean up:if nargout==0 clear hlin href htop hbotendend%% * * * * * * S U B F U N C T I O N S * * * * * * *function [x0,y0,iout,jout] = intersections(x1,y1,x2,y2,robust)INTERSECTIONS Intersections of curves. Computes the (x,y) locations where two curves intersect. The curves can be broken with NaNs or have vertical segments. Example: [X0,Y0] = intersections(X1,Y1,X2,Y2,ROBUST); where X1 and Y1 are equal-length vectors of at least two points and represent curve 1. Similarly, X2 and Y2 represent curve 2. X0 and Y0 are column vectors containing the points at which the two curves intersect. ROBUST (optional) set to 1 or true means to use a slight variation of the algorithm that might return duplicates of some intersection points, and then remove those duplicates. The default is true, but since the algorithm is slightly slower you can set it to false if you know that your curves don't intersect at any segment boundaries. Also, the robust version properly handles parallel and overlapping segments. The algorithm can return two additional vectors that indicate which segment pairs contain intersections and where they are: [X0,Y0,I,J] = intersections(X1,Y1,X2,Y2,ROBUST); For each element of the vector I, I(k) = (segment number of (X1,Y1)) + (how far along this segment the intersection is). For example, if I(k) = 45.25 then the intersection lies a quarter of the way between the line segment connecting (X1(45),Y1(45)) and (X1(46),Y1(46)). Similarly for the vector J and the segments in (X2,Y2). You can also get intersections of a curve with itself. Simply pass in only one curve, i.e., [X0,Y0] = intersections(X1,Y1,ROBUST); where, as before, ROBUST is optional.% Version: 1.12, 27 January 2010 Author: Douglas M. Schwarz Email: dmschwarz=ieee*org, dmschwarz=urgrad*rochester*edu Real_email = regexprep(Email,{'=','*'},{'@','.'})% Theory of operation: Given two line segments, L1 and L2, L1 endpoints: (x1(1),y1(1)) and (x1(2),y1(2)) L2 endpoints: (x2(1),y2(1)) and (x2(2),y2(2)) we can write four equations with four unknowns and then solve them. The four unknowns are t1, t2, x0 and y0, where (x0,y0) is the intersection of L1 and L2, t1 is the distance from the starting point of L1 to the intersection relative to the length of L1 and t2 is the distance from the starting point of L2 to the intersection relative to the length of L2. So, the four equations are (x1(2) - x1(1))*t1 = x0 - x1(1) (x2(2) - x2(1))*t2 = x0 - x2(1) (y1(2) - y1(1))*t1 = y0 - y1(1) (y2(2) - y2(1))*t2 = y0 - y2(1) Rearranging and writing in matrix form, [x1(2)-x1(1) 0 -1 0; [t1; [-x1(1); 0 x2(2)-x2(1) -1 0; * t2; = -x2(1); y1(2)-y1(1) 0 0 -1; x0; -y1(1); 0 y2(2)-y2(1) 0 -1] y0] -y2(1)] Let's call that A*T = B. We can solve for T with T = AB. Once we have our solution we just have to look at t1 and t2 to determine whether L1 and L2 intersect. If 0 <= t1 < 1 and 0 <= t2 < 1 then the two line segments cross and we can include (x0,y0) in the output. In principle, we have to perform this computation on every pair of line segments in the input data. This can be quite a large number of pairs so we will reduce it by doing a simple preliminary check to eliminate line segment pairs that could not possibly cross. The check is to look at the smallest enclosing rectangles (with sides parallel to the axes) for each line segment pair and see if they overlap. If they do then we have to compute t1 and t2 (via the AB computation) to see if the line segments cross, but if they don't then the line segments cannot cross. In a typical application, this technique will eliminate most of the potential line segment pairs.% Input checks.narginchk(2,5)% Adjustments when fewer than five arguments are supplied.switch nargin case 2 robust = true; x2 = x1; y2 = y1; self_intersect = true; case 3 robust = x2; x2 = x1; y2 = y1; self_intersect = true; case 4 robust = true; self_intersect = false; case 5 self_intersect = false;end% x1 and y1 must be vectors with same number of points (at least 2).if sum(size(x1) > 1) ~= 1 || sum(size(y1) > 1) ~= 1 || ... length(x1) ~= length(y1) error('X1 and Y1 must be equal-length vectors of at least 2 points.')end x2 and y2 must be vectors with same number of points (at least 2).if sum(size(x2) > 1) ~= 1 || sum(size(y2) > 1) ~= 1 || ... length(x2) ~= length(y2) error('X2 and Y2 must be equal-length vectors of at least 2 points.')end% Force all inputs to be column vectors.x1 = x1(:);y1 = y1(:);x2 = x2(:);y2 = y2(:);% Compute number of line segments in each curve and some differences we'll need later.n1 = length(x1) - 1;n2 = length(x2) - 1;xy1 = [x1 y1];xy2 = [x2 y2];dxy1 = diff(xy1);dxy2 = diff(xy2);% Determine the combinations of i and j where the rectangle enclosing the i'th line segment of curve 1 overlaps with the rectangle enclosing the j'th line segment of curve 2.[i,j] = find(repmat(min(x1(1:end-1),x1(2:end)),1,n2) <= ... repmat(max(x2(1:end-1),x2(2:end)).',n1,1) & ... repmat(max(x1(1:end-1),x1(2:end)),1,n2) >= ... repmat(min(x2(1:end-1),x2(2:end)).',n1,1) & ... repmat(min(y1(1:end-1),y1(2:end)),1,n2) <= ... repmat(max(y2(1:end-1),y2(2:end)).',n1,1) & ... repmat(max(y1(1:end-1),y1(2:end)),1,n2) >= ... repmat(min(y2(1:end-1),y2(2:end)).',n1,1));% Force i and j to be column vectors, even when their length is zero, i.e., we want them to be 0-by-1 instead of 0-by-0.i = reshape(i,[],1);j = reshape(j,[],1);% Find segments pairs which have at least one vertex = NaN and remove them. This line is a fast way of finding such segment pairs. We take advantage of the fact that NaNs propagate through calculations, in particular subtraction (in the calculation of dxy1 and dxy2, which we need anyway) and addition. At the same time we can remove redundant combinations of i and j in the case of finding intersections of a line with itself.if self_intersect remove = isnan(sum(dxy1(i,:) + dxy2(j,:),2)) | j <= i + 1;else remove = isnan(sum(dxy1(i,:) + dxy2(j,:),2));endi(remove) = [];j(remove) = [];% Initialize matrices. We'll put the T's and B's in matrices and use them one column at a time. AA is a 3-D extension of A where we'll use one plane at a time.n = length(i);T = zeros(4,n);AA = zeros(4,4,n);AA([1 2],3,:) = -1;AA([3 4],4,:) = -1;AA([1 3],1,:) = dxy1(i,:).';AA([2 4],2,:) = dxy2(j,:).';B = -[x1(i) x2(j) y1(i) y2(j)].';% Loop through possibilities. Trap singularity warning and then use lastwarn to see if that plane of AA is near singular. Process any such segment pairs to determine if they are colinear (overlap) or merely parallel. That test consists of checking to see if one of the endpoints of the curve 2 segment lies on the curve 1 segment. This is done by checking the cross product (x1(2),y1(2)) - (x1(1),y1(1)) x (x2(2),y2(2)) - (x1(1),y1(1)). If this is close to zero then the segments overlap.% If the robust option is false then we assume no two segment pairs are parallel and just go ahead and do the computation. If A is ever singular a warning will appear. This is faster and obviously you should use it only when you know you will never have overlapping or parallel segment pairs.if robust overlap = false(n,1); warning_state = warning('off','MATLAB:singularMatrix'); % Use try-catch to guarantee original warning state is restored. try lastwarn('') for k = 1:n T(:,k) = AA(:,:,k)B(:,k); [~,last_warn] = lastwarn; lastwarn('') if strcmp(last_warn,'MATLAB:singularMatrix') % Force in_range(k) to be false. T(1,k) = NaN; % Determine if these segments overlap or are just parallel. overlap(k) = rcond([dxy1(i(k),:);xy2(j(k),:) - xy1(i(k),:)]) < eps; end end warning(warning_state) catch err warning(warning_state) rethrow(err) end % Find where t1 and t2 are between 0 and 1 and return the corresponding % x0 and y0 values. in_range = (T(1,:) >= 0 & T(2,:) >= 0 & T(1,:) <= 1 & T(2,:) <= 1).'; % For overlapping segment pairs the algorithm will return an % intersection point that is at the center of the overlapping region. if any(overlap) ia = i(overlap); ja = j(overlap); % set x0 and y0 to middle of overlapping region. T(3,overlap) = (max(min(x1(ia),x1(ia+1)),min(x2(ja),x2(ja+1))) + ... min(max(x1(ia),x1(ia+1)),max(x2(ja),x2(ja+1)))).'/2; T(4,overlap) = (max(min(y1(ia),y1(ia+1)),min(y2(ja),y2(ja+1))) + ... min(max(y1(ia),y1(ia+1)),max(y2(ja),y2(ja+1)))).'/2; selected = in_range | overlap; else selected = in_range; end xy0 = T(3:4,selected).'; % Remove duplicate intersection points. [xy0,index] = unique(xy0,'rows'); x0 = xy0(:,1); y0 = xy0(:,2); % Compute how far along each line segment the intersections are. if nargout > 2 sel_index = find(selected); sel = sel_index(index); iout = i(sel) + T(1,sel).'; jout = j(sel) + T(2,sel).'; endelse % non-robust option for k = 1:n [L,U] = lu(AA(:,:,k)); T(:,k) = U(LB(:,k)); end % Find where t1 and t2 are between 0 and 1 and return the corresponding % x0 and y0 values. in_range = (T(1,:) >= 0 & T(2,:) >= 0 & T(1,:) < 1 & T(2,:) < 1).'; x0 = T(3,in_range).'; y0 = T(4,in_range).'; % Compute how far along each line segment the intersections are. if nargout > 2 iout = i(in_range) + T(1,in_range).'; jout = j(in_range) + T(2,in_range).'; endendend
⛳️ 运行结果
🔗 参考文献
🎈 部分理论引用网络文献,若有侵权联系博主删除
🎁 关注我领取海量matlab电子书和数学建模资料
👇 私信完整代码和数据获取及论文数模仿真定制
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化
2 机器学习和深度学习方面
卷积神经网络(CNN)、LSTM、支持向量机(SVM)、最小二乘支持向量机(LSSVM)、极限学习机(ELM)、核极限学习机(KELM)、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断
2.图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知
3 路径规划方面
旅行商问题(TSP)、车辆路径问题(VRP、MVRP、CVRP、VRPTW等)、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化
4 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化
5 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化
6 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化
7 电力系统方面
微电网优化、无功优化、配电网重构、储能配置
8 元胞自动机方面
交通流 人群疏散 病毒扩散 晶体生长
9 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


