新智元报道
编辑:编辑部
【新智元导读】陶哲轩的新论文,竟是用GPT-4辅助写的?前不久,GitHub Copilot的惊人能力已经让陶哲轩不安,现在,众大佬齐呼数学研究亟需AI协助。
今年6月,陶哲轩曾在博客中预言,2026年,AI将与搜索和符号数学工具相结合,成为数学研究中值得信赖的合著者。
这个预言,如今已经愈发成真。
就在6月底,加州理工、英伟达、MIT等机构的学者,曾构建了一个基于开源LLM的定理证明器。
最近,陶哲轩又发现,在使用Lean进行自然数游戏研究时,GPT-4竟然也起到一些作用。
在AI的辅助下,他得到了关于有限多个实变量不等式理论的成果,论文很快就会发在arXiv上。
如何用GPT-4研究自然数游戏
什么是自然数游戏?
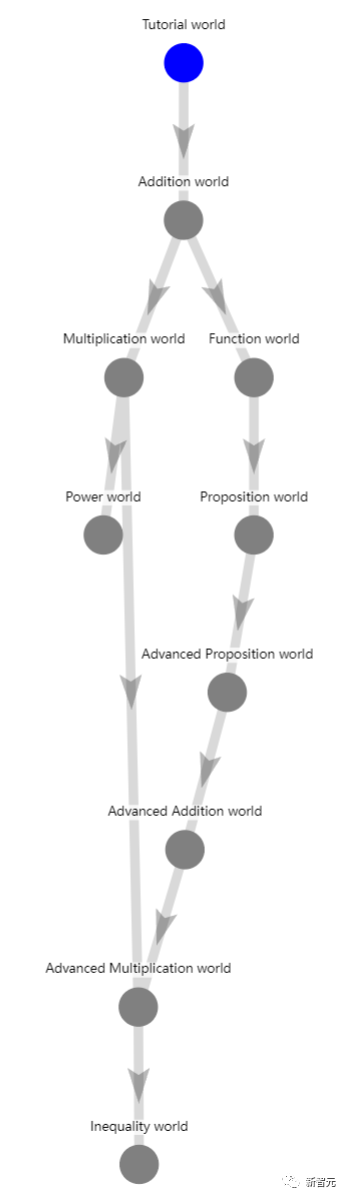
这个游戏,神奇地展示了归纳的力量。
如图所示,我们从蓝色节点上输入,而灰色节点上方的所有结点都完成时,灰色节点将变为蓝色。
在这个过程中,我们当然可以随时尝试任何级别的节点,但如果它是灰色的,我们可能就没有足够的知识来完成这个节点。

引理:对于所有自然数x、y和z都有xy+z=xy+z。证明开始!
在自然数游戏中,我们就会在定理证明器Lean中,得到自己的一个自然数版本——mynat。这个自然数满足了数学归纳定理,以及其他原理(比如皮亚诺公理)。

不过,问题在于,目前还没有人证明这些关于自然数的定理,比如,你可以定义加法,但还没有人证明x + y = y + x。
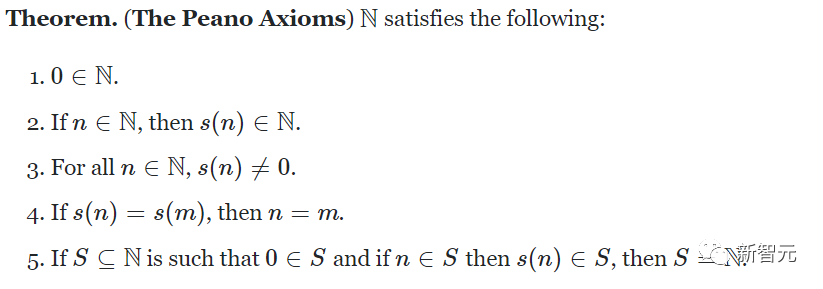
皮亚诺公理
而自然数游戏,就需要你解决游戏中的关卡,用Lean定理证明器来证明数学定理。

我们证明了n+0=n,这个证明被称为add_zero。但并不能证明zero_add,0+n=n。这两个定理不是一样吗?并非如此!事实上x + y = y + x,这是加法世界的BOSS级难题。
陶哲轩是出于怎样的机缘巧合,开始玩自然数游戏的呢?
原来,他是在IPAM机器辅助证明研讨会上看到过几次Lean的演示,并且被建议玩一玩自然数游戏,来熟悉Lean中用于证明定理的基本语法和策略。
让陶哲轩感到惊喜的是,这个游戏越玩越熟悉,因为它证明的结果和自己写的本科实分教材前几章的结果分成相似。

比如,从皮亚诺公理建立基本的算术事实,例如乘法的交换性和结合性。
另外,自然数游戏还让他想起了自己编码的逻辑游戏。
才玩了三个小时,陶哲轩就已经到达了「高级乘法」世界。他表示,在以后的空闲时间里他会继续玩这个游戏。

高级乘法世界:证明两个非零自然数的乘积为非零:a≠0 → b≠0 → a*b≠0
当然,GPT-4也知道Lean,它可以提供一些有用的回答。
不过,因为自然数游戏中可用的工具集很有限,所以GPT-4对于这个游戏没有直接的帮助,因为它提出的解决方案中涉及的方法,通常还没有被纳入游戏中。
不过,当他开始使用Lean的时候,GPT-4就变得非常有帮助了。

随着关卡变得越来越难,GPT的作用开始逐渐显现出来。
在Z显而易见是X和Y的结果的情况下,如果向GPT提问——
如果我已经知道X和Y,该如何证明Z呢?
这个过程就解决了各种微妙的语法问题,否则这些问题会十分令人沮丧。
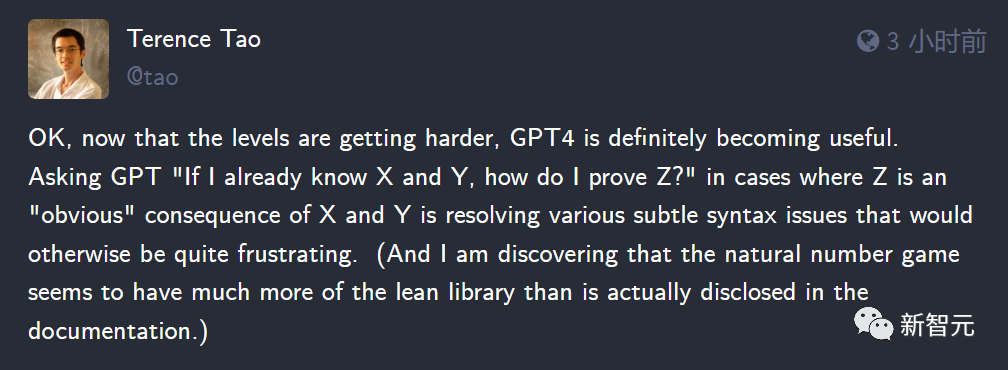
而且,陶哲轩发现,自然数游戏中包含的Lean库,似乎比文件中宣称的要多得多。
GitHub Copilot,让我不安
总之,AI工具辅助研究数学的奇迹,一次次让陶哲轩称赞不已,甚至发展到了让他「不安」。
前不久陶哲轩发现,GitHub Copilot已经能够预测到自己文章中数学论证的步骤了。
在10月初,陶哲轩表示,Github Copilot的能力惊艳到他了。
而且他强调,并不是它的编码能力,而是它编码之外的补充其他内容的能力,经常能让他喜出望外。
最近,他又称赞到——
我发现Github Copilot在我最近撰写博客文章的过程中出奇地有帮助。它能够正确预测该帖子中数学论证的几个步骤;在下面给出的示例中,我将积分分成三部分,并描述了如何估计第一部分,然后copilot正确地说明了如何估计其余两部分。
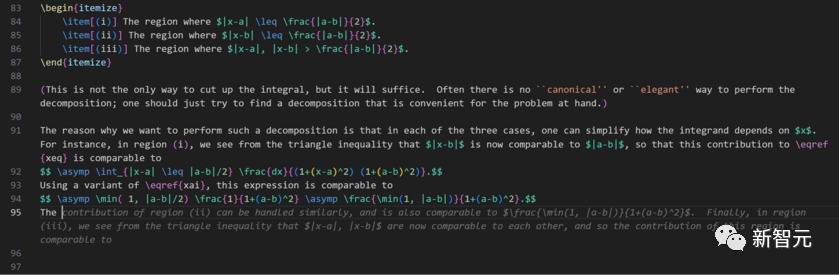
陶哲轩给出的例证
只要简单说明一下如何对第一部分进行估计,剩下的工作GitHub Copilot就能完成了,这也太惊艳了!
对此,陶哲轩的评价是:「Copilot的性能给我留下了深刻的印象(并且让我有点不安)」。
他补充说「虽然其中的许多建议并不那么合适,我估计Copilot可能建议了十几句话,最终以某种形式出现在我的博客文章中。」
而他说的博客文章就是这篇关于「非负量的和或积分的上界」。
博文地址:https://terrytao.wordpress.com/2023/09/30/bounding-sums-or-integrals-of-non-negative-quantities/
估计某个量的大小,是数分、概率论、组合学等领域中的常见问题,如估计函数、序列、结合等的和或积分。
因此陶哲轩这篇估计非负量的和或积分上界,探讨的正是数学领域的重要问题。

陶哲轩在博客中总结了3种估算大量非负量和以及积分的方法,如算术平均值-几何平均值不等式、Holder不等式、Markov不等式等。

其中的内容和代码没有关系,但是Github Copilot依然给出了让陶哲轩都感到惊叹的内容建议。

能让陶哲轩都感到有点不安的Github Copilot,源于Github和OpenAI的合作。
它主要功能是利用生成式AI的能力为程序提供编码的建议,自动补充等编码功能。而之所以它有如此强大的功能,和背后微软,OpenAI的大量投入是分不开的。
最近外媒报道,微软提供的Github Copilot每月10刀的订阅服务,在算力成本上,每个用户要让微软亏损20美元/月。

文章地址:https://www.wsj.com/tech/ai/ais-costly-buildup-could-make-early-products-a-hard-sell-bdd29b9f?mod=followamazon
这些服务成本如此高昂的原因之一,是使用了最强大的AI模型,与普通的软件或云服务相比,这些模型需要更多的电力,并对处理器的运行造成更大的压力。
文章中甚至将现在的AI工具的能力和成本做了一个让人绷不住的比喻:
「用AI去做文章总结就像开着兰博基尼去送披萨一样」。
足见现在科技巨头们,为了让用户充分享受AI带来的便利,真的是下了血本!
所以让陶哲轩惊叹的Github Copilot能在编码之外还有如此强大的能力,也似乎不那么奇怪了。
AI如何辅助数学研究
显然,现在所有人都已经意识到:AI具有巨大潜力,它可以通过指导猜想生成、协助形式化数学等方式为数学发展做出贡献。

在9月26日举行的一场关于使用AI辅助数学推理的网络研讨会上,众数学大咖云集,一起讨论了人工智能技术如何用于推进数学科学,跨学科合作如何开辟新的机会。
陶哲轩也参与了会议,并结合自己与AI合作的经历谈了自己的观点。

大会对于AI辅助数学研究,AI专家和数学家协作配合的新机会和新挑战,都展开了充分地讨论,可谓是干货满满:
尝试应用机器学习方法来辅助或完成形式数学论证,现在已经是人工智能应用的一个独特领域
AI在辅助数学研究中的独特之处在于,数学具有一种自我验证的方法,可以用来检查AI产生的结果,而其他AI任务通常需要人类参与来评估反馈的质量。
数学表达本身具有一种内在的准确性,因此机器学习在数学领域能够在数据相对稀缺的情况下有效地推进工作,这使得AI在数学领域具备明显的优势。
在研讨会上,多位数学领域专家进行了知识分享和交流。

在使用机器学习协助数学发现方面,会议中数学家Heather提到了具体的几个例子:

(1) DeepMind和数学家合作,利用机器学习从大量数据中寻找模式,形成了关于模形的新猜想。
(2) Sutherland等数学家也使用机器学习在模形式的工作中找到了新公式。
(3) Adam Wagner使用机器学习来寻找图论问题的反例。
(4) Javier Pena利用机器学习找到偏微分方程近似的数值解,以方便后续的严格数值方法的推进。
在使用AI辅助证明方面,会议提到形式化证明可以将一个大证明分解成小块,不同人可以负责不同部分。

这可能会开启新的科研协作模式——计算机可以自动化证明中的某些步骤,已经有许多前沿的数学领域使用了这种模式。
这种形式化证明的过程有利于数学家以新方式与AI进行创造性的互动。
这也体现了AI协助数学发现和传统数学研究的不同:既有大公司提供计算资源的大规模合作,也有小规模的个人之间的合作探索。
学界需要对这些不同的合作模式保持开放。

会议中,还有多位学者讨论了AI在数学翻译中的应用
数学翻译是指将一个数学问题从一个领域翻译到另一个领域的等价表达,这是数学家解决问题的基本工具之一。
数学家以一个图论问题为例。图论问题可以翻译成代数问题,两者逻辑上是等价的,但表达上的术语和形式明显不同。
AI转换工具可以将一个看似毫无头绪的问题,转化成一个可以用已有技术来解决的问题。
还有学者进一步指出,证明思路到形式证明的转换,以及形式证明到实际算法的转换,也是一种翻译过程。
鉴于AI在不同语言之间的翻译上取得了巨大进展,未来可以研究如何应用机器学习来实现数学领域内的翻译。
例如将不完整的证明草图自动翻译成可证明的形式表达。这是当前一个非常有前景的研究方向。
会议中多位数学家也强调了。由于数学翻译能显著拓展问题解决的视角,应用机器学习来实现数学翻译将可能大大推进数学研究。
AI专家和数学家进行跨界合作,需要面对的差异和挑战
AI界和数学界,存在着诸多差异。
比如,机器学习研究者习惯处理大规模数据集,而数学家习惯于处理相对较少的数据。机器学习研究者注重在一类任务上的平均表现,而数学家则更关注单个案例的解释。
另外,两者的出版文化不同,机器学习界会公开发表绝大部分研究内容,数学界则不然。机器学习界普遍第一作者为主要贡献者,数学界作者顺序就比较随机。
大规模合作项目的学术贡献认定上,二者也存在差异。形式化研究使得每个参与者只负责一小块,如何评价贡献是一个新问题。
还有一个差异,是资源获取方式。
机器学习需要大数据集和计算资源,数学家对这方面的需求就相对较少。如何使各界研究者公平获取资源也会是一个问题。开源文化不同。机器学习界更看重开源共享,而数学界不一定。如何处理二者关系需要考量。
由于这是一个全新的交叉领域,双方在一些根本理念和工作方式上存在差异,需要在合作中加以认识和调适,以实现更好的协同效果。
参考资料:https://mathstodon.xyz/@tao/111206761117553482






 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


