论文 | 一切皆可连接：图神经网络 | 大牛GAT作者Petar Velickovic最新综述

本文是大牛GAT作者Petar Velickovic在2023年结构生物学中的人工智能 (AI) 方法的一篇综述文章。

在许多方面，图是我们从自然界接收数据的主要形式。这是因为我们看到的大多数模式，无论是在自然系统还是人工系统中，都可以使用图结构语言来优雅地表示。突出的例子包括分子（表示为原子和键的图）、社交网络和运输网络。这种潜力已经被主要的科学和工业团体看到，其已经受到影响的应用领域包括流量预测、药物发现、社交网络分析和推荐系统。此外，前几年机器学习最成功的一些应用领域——图像、文本和语音处理——可以被视为图表示学习的特例，因此这些领域之间存在大量的信息交换。这项简短调查的主要目的是使读者能够吸收该领域的关键概念，并在相关领域的适当背景下定位图表示学习。

https://doi.org/10.1016/j.sbi.2023.102538

简介：为什么要研究图数据？

在本次调查中，我将介绍深度学习研究的一个充满活力且令人兴奋的领域：图表示学习。或者，简单地说，基于图（由边连接的节点的互连结构）上的数据构建机器学习模型。这些模型通常称为图神经网络，简称 GNNs。

有充分的理由研究图数据。从分子（通过化学键连接的原子图）一直到大脑的连接体结构（通过突触连接的神经元图），图是描述各个组织层次的生物体的通用语言。同样，人类感兴趣的最相关的人工构造，从交通网络（由道路连接的交叉口图）到社交网络（由友谊链接连接的用户图），最好用图来推理。

近年来，科学和工业团体都意识到了这一潜力，GNN 现在被用来发现新型强效抗生素、在 Google 地图中提供估计的旅行时间、在 Pinterest 中提供内容推荐和在 Amazon 中提供产品推荐，并设计最新一代 机器学习硬件：TPUv5。此外，基于 GNN 的系统帮助数学家揭示了数学对象的隐藏结构，从而在表示论领域提出了新的顶级猜想。毫不夸张地说，数十亿人每天都在接触 GNN 的预测。因此，研究 GNN 可能是一项有价值的追求，即使其目的不是直接为其发展做出贡献。

除此之外，在某种意义上，驱动我们推理和决策的认知过程很可能是图结构的。也就是说，套用一句话：没有人真正在头脑中想象出他们所知道的所有信息；相反，他们只想象选定的概念以及它们之间的关系，并使用它们来表示真实的系统。如果我们接受这种认知解释，那么如果没有某些依赖于图表示学习的组件，我们就不太可能构建一个通用的智能系统。请注意，这一发现与许多近期熟练的 ML 系统基于 Transformer 架构的事实并不冲突，正如我们将在这篇评论中发现的那样，Transformer 本身就是 GNN 的一个特例。

基本原理：排列等变性和不变性

在上一节中，我们了解了为什么研究图中的数据是个好主意。现在我们将了解如何通过图结构数据学习有用的函数。阐述大致如下。

对于图结构输入，我们通常假设一个图 G=(V, E)，即我们有一组边 E=V*V，它指定 V 中连接的节点对。

由于我们对节点上的表示学习感兴趣，因此我们为每个节点 u=V 附加一个特征向量，x^u=R^k。该数据呈现给机器学习模型的主要方式是采用节点特征矩阵的形式。也就是说，通过堆叠这些特征来准备矩阵 X=R^(|V|*k)：

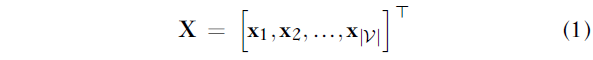
即X的第i行对应xi。

E的表示方法有很多种；由于我们的上下文是线性代数之一，因此我们将使用邻接矩阵 A=R^(|V|*|V|)：

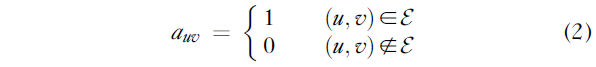
请注意，通常有可能，特别是在生化输入中，我们希望将更多信息附加到边（例如距离标量，甚至整个特征向量）。我故意不考虑此类情况，以保持清晰——我们在这些情况下得出的结论是相同的。

然而，使用上述表示的行为本身就强加了节点排序，因此是一个任意选择，与无序的节点和边不对齐！因此，我们需要确保排列节点和边（PAP^T，对于排列矩阵 P）不会改变输出。我们恢复 GNN 必须满足的以下规则：

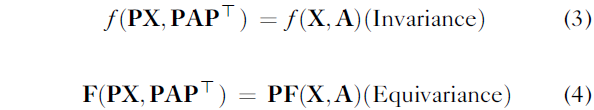
在这里，为了简单起见，我们假设函数 f，F 不会改变邻接矩阵，因此我们假设它们仅返回图或节点级输出。

此外，图的边允许这些函数中的局部性约束。就像 CNN 在图像每个像素的小邻域上运行一样，GNN 也可以在节点的邻域上运行。定义该邻域 N_u 的一种标准方法如下：

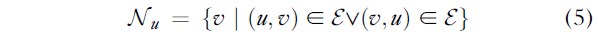
因此，我们可以定义所有邻域特征的多重集 X_N_u ：

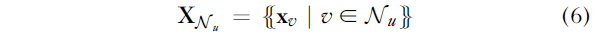
我们的局部函数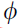可以考虑邻域，即：

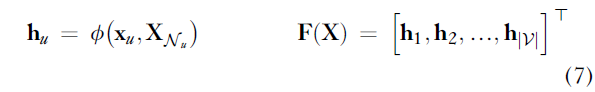
通过简单的线性代数操作，可以证明如果 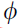在 X_N_u 中是排列不变的，那么 F 将是排列等变的。剩下的问题是，我们如何定义？

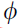图神经网络

不用说，定义 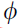是当今机器学习研究最活跃的领域之一。根据文献上下文，它可以被称为“扩散”、“传播”或“消息传递”。正如所声称的；其中大多数可以分为三种空间风格之一：

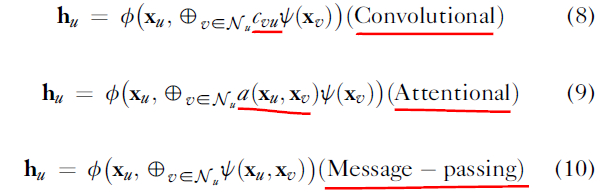
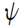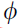其中和 是神经网络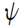(x) = ReLU(Wx + b)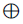，是任何排列不变聚合器，例如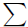、平均或最大值。GNN 的表达能力从方程（8）-（10）开始逐渐增强，但代价是可解释性、可扩展性或学习稳定性。对于大多数任务，在选择正确的形式时需要仔细权衡。

本综述并不试图全面概述特定的 GNN 层。话虽这么说：代表性的卷积 GNN 包括切比雪夫网络; (ChebyNet)，图卷积网络; (GCN)和简化图卷积; (新加坡GC); 代表性的注意力 GNN 包括混合模型 CNN; (MoNet)，图注意力网络; (GAT) 及其最近的“v2”变体; (GATv2); 代表性的消息传递 GNN 包括交互网络; (IN)，消息传递神经网络; (MPNN)和图网络; (GN)。

给定这样一个 GNN 层，我们可以通过适当组合 h_u 在图上学习任何有趣的任务。我以生物学例子为基础，举例说明了三项主要的此类任务：

节点分类。 如果目标是预测每个节点 u=V 的目标，那么我们的输出是等变的，我们可以直接在 h_u 上学习共享分类器。一个典型的例子是在给定的蛋白质-蛋白质相互作用网络中对蛋白质功能进行分类（例如使用基因本体数据），这首先是由 GraphSAGE 完成的。

图分类。如果我们想要预测整个图的目标，那么我们需要一个不变的输出，因此需要首先将所有 h_u 简化为通用表示，例如通过执行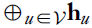，然后在生成的平面向量上学习分类器。一个典型的例子是根据分子的量子化学特性对其进行分类，估计药理学特性，如毒性或溶解度或虚拟药物筛选。

链接预测：最后，我们可能对预测边（u，v）的属性感兴趣，甚至预测边是否存在；从而产生了“链接预测”这个名称。在这种情况下，可以通过特征 h_u || h_v 以及任何给定的边级特征的串联来学习分类器。典型任务包括预测药物和疾病之间的联系、药物再利用、药物和靶标、结合亲和力预测，或药物和药物、预测复方用药的不良副作用。

可以使用上述主要任务中的构建块来超越对输入图给出的实体进行分类的范围，并拥有产生新分子甚至进行逆合成的系统——估计用于合成给定分子的反应。

在对集合进行类似讨论之后，自然会出现一个问题：如方程 (10) 所示，GNN 是否表示图上所有有效的排列等变函数？意见分歧。前几年的主要结果似乎表明，此类模型从根本上限制了它们可以解决的问题。然而，大多数（如果不是全部）解决这些限制的建议仍然可以使用等式（10）的成对消息传递形式来表达；主要要求是仔细修改应用方程的图。为了进一步补充这一点，表明在适当的初始特征、足够的深度宽度乘积（#layers * dim h_u）以及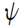和 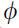 的正确选择下，等式（10）中的GNN是图灵通用的——可能能够模拟任何计算机可以对此类输入执行的任何计算。

考虑到所有要点，作者认为本节中的形式主义很可能是我们构建强大的 GNN 所需的全部，当然，不同的观点可能有益于不同的问题，并且强大的 GNN 的存在并不意味着很容易找到使用随机梯度下降。

没有图的 GNN：深度集和 Transformer

在上一节中，我们做了一个看似无辜的假设：我们得到了一个输入图（通过 A）。然而，很多时候，我们不仅不会对 A 做出明确的选择，而且我们可能对 A 是什么也没有任何先验的信念。此外，即使给出一个没有噪声的真实值 A，它也可能不是最优的计算图：也就是说，通过它传递消息可能会出现问题——例如，由于瓶颈。因此，研究能够调节输入图结构的 GNN 通常是一种有用的追求。

因此，我们假设我们只有一个节点特征矩阵 X，但没有邻接。一个简单的选项是“悲观”选项：假设根本没有边，即 A = I，或 N_u = {u}。在这样的假设下，方程（8）-（10）都简化为 h_u = 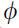(x_u)，产生 Deep Sets 模型。因此，这里没有利用基于图的建模的能力。

相反的选项（“惰性”选项）是假设一个完全连接的图；即 A = 11^T，或 N_u = V。这使得 GNN 能够充分利用任何被认为合适的边，并且对于较少数量的节点来说是一个非常受欢迎的选择。可以看出，在这种情况下，卷积 GNN（方程（8））仍然会简化为深度集，这促使使用更强的 GNN。层次结构中的下一个模型是注意力 GNN（方程（9）），可简化为以下方程：

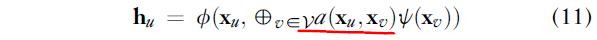
这本质上是 Transformer 的前向传播。为了逆向分析 Transformer 出现在这里的原因，让我们考虑 NLP 的角度。即，句子中的单词相互作用（例如主语-宾语，副词-动词）。此外，这些交互不是微不足道的，当然也不是连续的，也就是说，即使单词相隔很多句子，它们也可以交互。因此，我们可能想在它们之间使用图。但这个图是什么？甚至注释者也不愿意达成一致，并且最佳图很可能取决于任务。在这样的设置中，一个常见的假设是使用完整的图，并让网络自行推断关系——此时，Transformer 几乎被重新导出。进行深入的重新推导。

Transformer 成为如此主导的 GNN 变体的另一个原因是，使用完全连接的图结构允许使用密集矩阵乘积来表达所有模型计算，因此它们的计算与当前流行的加速器（GPU 和 TPU）非常吻合。此外，它们比消息传递变体（公式（10））具有更有利的存储复杂性。因此，Transformers 可以被视为目前赢得硬件彩票的 GNN！

在结束本节之前，值得注意的是在没有输入图的情况下学习 GNN 的第三种选择：推断用作 GNN 边的图结构。这是一个被称为潜在图推理的新兴领域。这通常是相当具有挑战性的，因为边选择是一种不可微分的操作，并且近年来提出了各种范式来克服这一挑战：非参数学习、监督学习、变分学习、强化学习和自监督学习。

超越排列等方差的 GNN：几何图

为了结束我们的讨论，我们重新审视另一个假设：我们假设我们的图是离散的、无序的、节点和边的集合，仅容易受到排列对称性的影响。但在很多情况下，这并不是故事的全部！事实上，该图通常可能被赋予一些空间几何形状，这对于利用起来非常有用。分子及其三维构象异构体结构就是一个典型的例子。

一般来说，我们假设我们的输入是几何图：节点被赋予特征 f_u 和坐标 x_u=R^3。我们可能有兴趣设计一个不仅与排列等变，而且与 3D 旋转、平移和反射等变的模型（欧几里得群，E(3)）。

E(3) 等变消息传递层转换坐标和特征，并产生更新的特征 f_u’ 和坐标 x_u’。存在许多遵循 E(n) 等方差的 GNN 层，一种特别优雅的解决方案是：

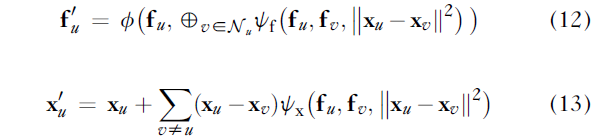
该模型背后的关键见解是旋转、平移或反射坐标不会改变它们的距离 ||x_u – x_v||^2，即此类操作是等轴测。因此，如果我们将所有节点旋转转换为 x_u <- Rx_u + b，则输出特征 f_u’ 保持不变，而输出坐标相应地变换：x_u’ <- Rx_u’ + b。

虽然确实非常优雅，但像这样的模型隐藏了一个警告：它仅适用于标量特征 f_u。如果我们的模型需要支持任何类型的向量输入（例如原子之间的力），则方程（12）中的模型是不够的，因为向量需要随 R 适当旋转。确实提出了一种允许显式更新向量的变体特征，v_u：

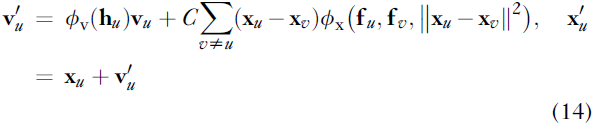
但随着功能变得“紧张”，这些问题将继续出现。因此，在这种情况下，表征支持所有可能的旋转平移等变模型的通用方程，然后学习其参数可能会很有用。这种分析是在张量场网络中针对点云进行的，然后扩展到针对一般图的 SE(3)-Transformers。

也许这项调查的一个合适的结论是一个简单的认识：在展示了 Transformer 和几何等方差约束如何在 GNN 的背景下发挥作用之后，我们现在拥有了定义一些最著名的几何 GNN 架构的所有关键构建块。例如 AlphaFold 2，但也有类似的蛋白质相关文章，这些文章在《自然方法》中都成为了头条新闻；MaSIF）和自然机器智能。蛋白质折叠、蛋白质设计和蛋白质结合预测似乎都是几何 GNN 的一个极其有效的攻击领域；这只是结构生物学领域将从这些最新发展中受益的众多坚实原因之一。

微信群                   公众号