导语

1950年，后来被誉为“计算机科学之父”和“人工智能先驱”的艾伦·图灵（Alan M. Turing）发表了划时代论文《计算机器与智能》（Computing Machinery and Intelligence），探讨“机器是否能思考”这一根本问题。文中图灵设计了“模仿游戏”（Imitation Game）的思想实验，这就是后世广为人知的“图灵测试”。然而，透过“图灵测试”的光环仔细研读，会发现图灵在文中表达了对机器与智能远远更为深刻的思考。为此集智俱乐部AGI社区对这篇经典论文做了完整翻译，希望能够回归本源，探讨其丰厚内涵，也希望对读者有所启发。
研究领域：人工智能，图灵测试，模仿游戏，学习机器Alan M. Turing | 作者何瑞杰、徐博文、刘兆庭、冯睿洋 | 翻译徐博文 | 审校梁金 | 编辑

论文题目：Computing Machinery and Intelligence论文地址：https://academic.oup.com/mind/article/LIX/236/433/986238
目录

1. 模仿游戏

2. 对新问题的批评

3. 模仿游戏中的机器

4. 数字计算机

5. 数字计算机的通用性

6. 关于主要问题的争议

7. 学习机器

1. 模仿游戏

考虑以下问题：“机器能思考吗？”（Can machines think?）要回答这个问题，首先需要定义“机器”和“思考”这两个术语。定义的表述或许要尽可能反映这两个词的通常用法，但这种看法是危险的。如果我们通过考察这两个词的通常用法来找到它们的含义，那么很难避免得出这样的结论：这两个词的含义和“机器能思考吗”这一问题的答案，将在“盖洛普民意测验”之类的统计调查中寻求。这是荒谬的。我并不试图给出这样的定义，而是提出另一个问题，它与原问题密切相关，并用相对清晰的词汇表达。

新的问题可以通过一个游戏来描述，称之为“模仿游戏”（imitation game）。游戏中有一个男人（A）、一个女人（B）和一个提问者（C，不论男女）。提问者待在一个与另外两人相隔离的屋子里，其目标是判断出外面哪个是男人、哪个是女人。提问者用标签 X、Y 指称外面的两个人。游戏结束时，他要说出“X 是 A，Y 是 B”或者“X 是 B，Y 是 A”。例如，提问者 C 可以向 A 和 B 提出下面这样的问题：

C：请 X 告诉我你头发的长度。

现在假如 X 实际上是 A，那么 A 必须回答。A 在游戏中的目标是努力使 C 做出错误的判断，他的回答可能是：

A：我留短发，最长的一缕大约有 9 英寸长。

为了防止人声帮助提问者得出结论，问题的回答应该写出来，或最好是打印出来：理想的安排是，让两个屋子用远程打印通信，或通过中间人传递问题和答案。而 B  在这个游戏中的任务是努力帮助提问者 C，她的最优策略可能就是如实回答。她可以在她的回答中加入“我是女的，别听他的”这样的话，但是这毫无用处，因为男人 A 同样也能说类似的话。

现在提出这样一个问题，“如果用机器代替 A，将会发生什么情况？”（What will happen when a machine takes the part of A in the game?）和 A、B 分别是两个人的时候相比，当 A  是机器时，提问者判断错误的频次会有所不同吗？这些问题将替换原问题“机器能思考吗”。

2. 对新问题的批评

人们可能不仅仅会问“新问题的答案是什么”，还可能问“这个新问题是否值得研究”。我们首先探讨第二个问题，以避免陷入无休止的递归（This latter question we investigate without further ado, thereby cutting short an infinite regress）。

这个新问题的优势在于，其在一个人的体力和智力之间划出一条相当清晰的界线。没有任何工程师或化学家声称能够生产出与人的皮肤完全相同的材料。即使在未来的某一天，这可能成为现实，但试图用这种人造皮肤来装扮一个“思维机器”以使它更像人类也是没有意义的。这种规则防止了提问者看到、接触到或听到其他人，该游戏的其他优势可在下面的示例中看出：

问：请写一首以福斯桥[1]为主题的十四行诗 (sonnet)。答：我还是算了。我从不写诗。问：34957 + 70764 等于多少？答：(停顿 30 秒后给出答案) 105621。问：你会下国际象棋吗？答：会。问：我的王在 K1，没有其他棋子，你只有一个王在 K6，一个车在 R1。现在该你走，你怎么走?

答：(停顿 15 秒) 车移动到 R8，将军。

这种问答方式似乎适用于我们所希望囊括的人类活动的任何领域。我们不希望机器因为在选美比赛中失利而受罚，正如我们不希望人类因为在与飞机的竞速中失败而受罚一样。这种游戏设置使得这些“无能”变得无关紧要：只要参与者认为合适，他们可以夸耀他们的魅力、力量或勇气，而提问者不能要求他们做实际的展示。

这个游戏可能会受到一些批评：“机器的胜算太大了。”(The odds are weighted too heavily against the machine）如果一个人试图冒充机器，他显然会表现得很差。他可能会因为做算术缓慢和不准确而立马露馅。难道机器不会做某些应该被说成思维但和人所做的很不同的事吗？这是个很有力的反对意见，但我们至少可以说，如果能够成功地玩模仿游戏的机器可以被构造出来，我们无需为这种反对意见而烦恼。[2]

有人可能会指出，在玩“模仿游戏”时，机器的最佳策略也许不是模仿人类的行为。这是可能的， 但我认为这无伤大雅。在任何情况下，这里不打算研究博弈的理论（theory of the game），并且假定机器的最佳策略是努力提供人会自然给出的回答。

3. 模仿游戏中的机器

只有在我们明确了“机器”这个词的含义之后，第一节中提出的问题才能被明确解答。当然，我们期望任何一种技术都可用于我们的机器。同时，我们也愿意接受这种可能性：一位或一组工程师采用主要是实验的方法，制造出一个可运行的机器，但却不能很好地描述其工作方式。最后，我们希望自然方式出生的人不被归类为机器。让定义同时满足这三个条件是具有挑战性的。例如，你可能要求这些工程师是同一性别[3]。但实际上，这也无法令人满意，因为即使通过个体的一个皮肤细胞也许可以产生一个完整的生命体——这将是生物科技具有划时代意义的突破——但我们不会将其视为“构建思维机器”的情形。这迫使我们放弃“允许任何一种技术”这一要求。我们更倾向于此，因为当前“思维机器”的研究主要集中在一种通常被称为“电子计算机”或“数字计算机”的特殊机器上，因此，我们只允许“数字计算机”参与我们的游戏。

这种限制乍看过于严格，但我将尝试说明实际情况并非如此。为此，须简要说明这些计算机的本质和特性。

有人可能会说：将机器与数字计算机等同起来，就像我们对“思考”的标准一样，可能是不具说服力的，因为这可能会证明数字计算机无法在模仿游戏中表现出色（这与我的信念相反）。

目前已经有许多数字计算机在运行，人们可能会问：“为什么不直接进行实验呢？这样很容易满足游戏的要求。让许多提问者同时参与游戏，然后统计出判断正确的概率”。对这个问题的简要回答是：我们并不是在问是否所有的数字计算机都能在游戏中表现出色，也不是在问是否有现有的计算机能够通过实验，而是在问：是否存在可以想象到的计算机能够通过游戏。这只是一个简要回答，我们稍后将从不同的角度来考察这个问题。

4. 数字计算机

数字计算机可被理解为能够执行任何人类计算员能够完成的操作。一个人类计算员应该严格遵守规则，不得偏离。我们可以假设这些规则写在一本书上，每次被分配新的任务时，这本书中指令的执行顺序将被更改。他有无限的纸进行计算，也可以用“台式机器”进行乘法和加法运算，但这并不重要。

若使用上述解释定义数字计算机，我们将面临循环论证的危险。为此，我们通过概述我们预期数字计算机能达到的效果来避免这种情况。一个数字计算机通常由以下三个部分组成：

• 存储器（Store）
• 执行器（Executive unit）

• 控制器（Control）

存储器用来存储信息，对应于计算员的纸，计算员既可以在纸上计算，或是使用这些纸打印计算规则书。在计算员进行心算的情况下，一部分存储器将对应于他的记忆。

执行器是一次计算中各种单步操作进行的地方，这些操作随着机器而变化。比如一个较长的操作可能是“3540675445 乘以 7076345687”，但是一些机器可能只执行“写下 0”一类的简单操作。

上面曾经提到计算员的“规则书”由机器中的一部分存储器代替，不妨把它们称为“指令表” (Table of instructions)。控制器的功能就是保证指令按照正确的顺序执行，而其结构就是要确保这一点。

存储器中的信息通常被分解成大小适中的数据块，例如在一个机器中，一个数据块由十个十进制数组成，数据以某种方式被分配到存储单元中。一个典型的指令可以是：

“把存放在 6809 的数加上存放在 4302 的数，并把结果存入后面的存储单元。”

显然，此指令不会用英语表达，而是更有可能编码成“6809,4302,17”这样的形式，这里，17 表示对这两个数进行什么操作，在此就是“加法操作”。请注意，指令共占用了 10 个数字，因此正好是一个数据块，非常方便。控制器保证指令按照它们在指令表中的存储顺序被执行，但偶尔会碰到这样的指令：

“现在执行存储在 5606 的指令，并从那里继续执行。”

或者“如果 4505 位置是 0，那么执行存储在 6707 的指令，否则继续”。

后面这种指令非常重要，因为它能让一段操作序列重复执行、直到某种条件被满足，但这样做时，不是通过每次重复时执行新的指令，而是一遍又一遍执行相同的指令。可以类比为生活中的情景：如果妈妈想让汤姆每天上学时都到鞋匠那里看看她的鞋是不是修好了，妈妈可以每天都告诉他一遍；另一种方式是，在一个汤姆每天上学都能看到的地方贴个便条，告诉他到鞋匠那里去看一下，当汤姆拿回鞋时，就撕掉那个便条。

读者必须接受数字计算机可以，而且事实上就是按照我们所提出的原则建造的，几乎完全能够模仿一个人类计算员的行为。

当然，上面描述的人类计算员所使用的规则书仅仅是为了方便叙述虚构的，实际中计算员记得住他要做什么。如果一个人想让机器模仿计算员执行复杂的操作，他必须告诉计算机如何做，并把结果翻译成某种形式的指令表。这种构造指令表的行为通常被称为“编程”，“给一个机器编程使之执行操作 A”，意味着把合适的指令表放入机器以使它能够执行 A。

数字计算机的一个有趣变体是“带有随机元素的数字计算机”，它们有特定的指令进行掷骰子或者别的等价的电子学过程，例如一个指令可能是“掷那个骰子并把结果存入编号为 1000 的位置”。有时这样的机器被描述为具有自由意志（尽管我自己并不使用这种表达），但我们通常并不能通过观察判断出一台机器是否有随机元素，因为类似的效果可以通过诸如将选择依赖于的小数位数的设备来产生。

大多数现实中的数字计算机仅有有限的存储空间，让一个计算机具有无限的存储空间并不存在理论上的困难，当然在任何时候都只有有限的部分被使用。同样，制造出的计算机都只有有限的存储空间，但我们可以想象越来越多的存储空间可以根据要求添加。这样的计算机具有特殊的理论价值，我们称之为无限容量计算机。

有关数字计算机的设想很早就产生了。1828 到 1839 年担任剑桥大学的 Lucasian 数学教授的 Charles Babbage 设想了一个这样的机器，并称之为分析机（Analytical Engine），但并没有完成。尽管 Babbage 有了所有的基本想法，他的机器在那个时代却没有引人注目的前景，它能够达到的运算速度肯定比一个计算员要快，但比曼彻斯特机（Manchester Machine）慢 100 倍，而后者也是现代计算机中相当慢的一个，分析机的存储全部由用轮子和卡片组成的机械结构实现。

事实上，仅由机械结构实现的 Babbage 分析机帮助我们破除了一个迷信。现代数字计算机是电子的，神经系统也是电子的，这一事实常常被过分强调了。既然 Babbage 的机器没有使用电，而且所有的数字计算机在某种意义上都是等价的，那么我们就会明白是否使用电在理论上并不重要。当然，通常高速运算需要用电信号，因此，我们就会发现在这些地方使用电信号是理所当然的。在神经系统中， 化学过程至少和电过程同样重要。某些计算机的存储器主要基于声学原理。因此，计算机和神经系统都使用电仅仅是表面的相似。如果我们希望寻找相似性，倒不如寻找功能上的数学相似性。

5. 数字计算机的通用性

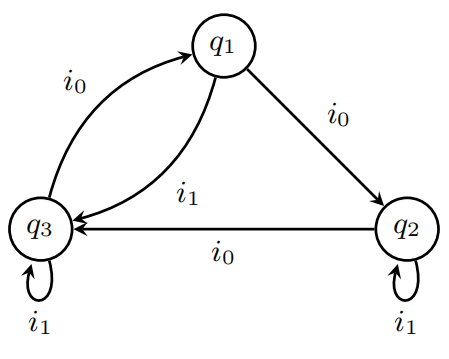
前文中考察的数字计算机可被归类为“离散状态机”，这类机器能够从一个确定状态跳变至另一个确定状态。这些状态的区别足够显著，以至于我们可以忽略它们之间可能的混淆。严格来说，这样的机器实际上并不存在。一切事物实际上都是连续变化的。然而，有很多种机器可以被视为离散状态机。例如，在照明系统中的开关，我们可以将开关看作只有开和关两个状态。它们之间肯定存在中间状态，但在大多数情况下我们可以忽略这些中间状态。作为离散状态机的一个例子，考虑一个每秒转 动 120 度的轮子，这个轮子可能会因为外部操纵杆而停止转动。在轮子上有一个发光的灯。这个机器可以抽象描述如下。机器的内部状态（通过轮子的位置来描述）可以是 q1，q2 或 q3，输入信号是 i0 或 i1（操纵杆的位置）。如下图所示，任何时候内部状态都可以由上一状态和输入信号决定，如下表所示。

这个例子是一个典型的离散状态机，只要它们的状态是有限的，就可以用这样的表格描述。[4]

可以看出，只要给出初始状态和输入信号，所有的未来状态都是可以预测的。这让人联想到拉普拉斯（Laplace）的观点，即只要给出某一时刻宇宙的完整状态（由所有粒子的位置和速度描述），就应该能预知未来的所有状态。但我们考虑的预测与拉普拉斯相比更接近实用性。对于“整个宇宙”这一系统，只要初始条件有一个很小的误差，后果将会截然不同。某个时刻一个电子位置的十亿分之一厘米的偏移，将决定一个人会在雪崩中死去还是逃生。我们称之为“离散状态机”的机械系统的一个基本特性是，这样的现象不会发生。即使是考虑实际的物理机器而不是理想化的机器，只要有关于某个时刻的状态的准确知识，就能得到任意未来时刻的准确知识。

正如我们之前提到的，数字计算机属于离散状态机，但是这样的机器所能够达到的状态集合通常是相当大的。例如，现在在曼彻斯特机可以有 2165000 个状态，也就是大约 1050000。而上面描述的轮子仅有 3 个状态。找到有如此多状态的原因并不困难，计算机具有一个存储器，对应于计算员的纸，这些存储器中应该能够写入任何能够写入计算员所用纸上的符号。为了简单起见，假设仅仅用从 0-9  的数字作为符号，忽略手写笔迹的差别。假如计算机具有 100 张每张 50 行，每行 30 个数字的存储空间，那么状态的数目将是 10(100×50×30)，即 10150000，这大约是 3 个曼彻斯特机状态数量的总和。状态数的以 2 为底的对数通常被称为机器的“存储容量”，因此曼彻斯特机的存储容量是 165000，而上面例子中轮子的存储容量是 1.6。如果两个机器加在一起，它们的存储大小应该是原来存储大小的和。因此 我们可以说“曼彻斯特机具有 64 个容量是 2560 的磁带存储器、8 个容量为 1280 的电子管。各种各 样存储器加在一起大约是 300 个，总容量共 174380”。

只要给出对应于离散状态机的状态转换表，就能够预测出机器将会做什么。这样的计算没有理由不能通过数字计算机来完成。只要运行足够快，数字计算机就能够模拟任何离散状态机的行为。模仿游戏可以变成在前面问题中的机器（B）和数字计算机（A）之间进行，并且提问者将不能区分它们。当然，数字计算机除了必须有足够的存储空间，且运行足够快。并且，模仿不同的机器之前，它（数字计算机）必须被重新编程。

由于数字计算机可以模拟任意离散状态机的性质，它可称为“通用机器（universal machines）”。具有这样性质的机器带来一个重要结果就是，除了对运行速度的考虑，不必设计出不同的新机器来执行不同的计算过程。不同计算过程都可以用同一个数字计算机来实现，只要根据不同情况适当编程。由此可见，所有数字计算机在某种意义上是等价的。

我们现在可以重新考虑在第三章末尾提出的问题。第三节中初步提出了将问题“机器能思考吗？”替换为“是否存在可想象其在模仿游戏中表现出色的数字计算机？”（Are  there  imaginable  digital computers which would do well in the imitation game?），如果愿意，我们还可以问“是否存在表现出色的离散状态机？”（Are there discrete state machines which would do well?），但是考虑到（数字计算机的）通用特性，我们可以看出这两个问题都等价于这一问题：“让我们把注意力集中在一个数字计算机 C 上，如果我们可以让其具有足够大的存储空间，足够快的计算速度，而且对它进行适当的编程。C 扮演角色 A，人扮演角色 B，C 能不能在模仿游戏中表现出色？”

6. 关于主要问题的争议

当前，我们可以认为基础问题已经整理清楚，准备对“机器是否能够思考？”以及上一章结尾的引申问题展开辩论。我们并不能完全放弃问题的原始形式，因为对所替代的问题的合理性会存在不同的看法，至少我们应该听取这方面的意见。

如果我首先解释我的看法，可能会让读者觉得更加明了。首先，让我们来看看这个问题更确切的形式。我相信，大约 50 年后，人们将有可能对存储容量将达到 109 左右的计算机进行编程，使其在模仿游戏中表现出色，以至于一般提问者在提问 5 分钟后准确判断的几率不会超过 70%。我相信，这时“机器能思考吗”这个就没有什么意义、不值得讨论了。尽管如此，我认为到本世纪末，语词用法和常识观点（general educated opinion）会有很大变化，因而人们能够谈论机器思维而不会受到反驳。我也相信，隐瞒这些信念没有任何好处。人们普遍认为科学家进行科学研究总是从可靠的事实导出可靠的事实，不受任何未经证明的猜想（conjectures）所影响。然而，这种看法实际上是错误的，只要能清晰地划分哪些是经过证明的事实，哪些是猜想，就不会有害处。猜想往往是非常重要的，因为它们提示了有用的研究方向（lines of research）。

现在开始考虑与我相反的意见。

6.1 神学上的异议

思考是人类不朽灵魂的一项特质，上帝赋予每个男人和女人一颗不朽的灵魂，但从未将其赋予其他动物或机器。因此，动物或机器无法进行思考。

尽管我无法接受这种观点，但我试图以神学的术语进行回应。如果将动物和人划分为一个范畴，我认为这个观点更为有说服力，因为在我看来，生物与非生物之间的差异远远大于人与其他动物之间的差异。如果站在其他宗教团体成员的立场上看，这种正统观点的武断性可能更为明显。伊斯兰教认为妇女没有灵魂，基督教对此有何感想？但我们暂时不深入讨论这一点，让我们回到主要争论上。在我看来，上文引述的论据对上帝全能的观念有相当大的限制：它承认上帝在某些方面也是无能为力的，比如，他不能让 1 = 2。但我们难道不应该相信，只要他认为合适，他就有自由赋予大象灵魂吗？我们或许可以预期上帝通过自己的力量，让大象拥有更为发达的大脑，以满足灵魂的需求。类似的论点也可以用在机器上。这可能看起来有所不同，因为它更难以让人接受（It may seem different because it is more difficult to “swallow”.）。但这实际只是意味着我们认为上帝不大可能考虑赋予灵魂的合适环境，有关情况将在后文中进一步讨论。在试图制造这样的机器时， 我们不应该无礼地剥夺上帝创造灵魂的权能，就如同我们不应该剥夺我们生育子女的权利一样。不论是制造机器还是生育，我们实际上都是上帝意志的工具，为他所创造的灵魂提供住所。

然而，这只是一种猜测。我对神学上的论据不太感兴趣，不管它们可能被用来支持什么论点。以往这些论据常常不能令人满意。在伽利略（Galileo）时代，有人主张：“日头在天当中停住，不急速下落，约有一日之久。”（《约书亚记（Joshua）》，10:13）以及“将地立在根基上，使地永不动摇。”（《诗篇（Psalm）》，104:5）这些经文充分反驳了哥白尼（Copernicus）的理论。从我们今天的知识来看，这样的论证是徒劳无益的。若没有这些知识，给人的感觉就大不相同了。

6.2 “鸵鸟”式的异议

“机器能思考的后果太可怕了，但愿它们不会思考。”这种论点可能没有上面表达得那么直白，但它影响到了我们大多数人（我们或多或少会如上那么想）。我们通常倾向于相信人类以某种微妙的方式比其他生物更为卓越。如果能够证明人类确实是地球上最高级别的存在，那再好不过，因为这样一来，我们就不必担心失去那至高无上的地位。这种感觉与神学的立场紧密相连，特别是在知识分子中更为流行，因为他们更注重思维力量，更倾向于相信人类在这方面的能力是无可比拟的。

我认为这个观点不值一驳。大概寻找些宽慰之词更恰当：或许这应该在灵魂轮回中寻找。

6.3 数学上的异议

在数理逻辑中的许多结果可用来指出离散状态机的能力局限，其中最著名的是哥德尔定理（Gödel’ s theorem）。该定理声称，在任何“足够强大”的逻辑系统中都有一种陈述，在该系统中既不能被证真，也不能被证伪，除非该系统本身是不一致的（Gödel 不完备定理。任何包含一阶谓词逻辑与初等数论的形式系统都存在一个命题，在该系统中无法被证明为真或假。）。邱奇（Church）、克林（Kleene）、罗瑟（Rosser）和图灵（Turing）等人也得到了类似的结果。图灵的结果最容易理解，因为它直接涉及到机器，而其他人的结果相对来说是间接的：例如，如果要使用哥德尔定理，我们还需要有一些用机器来描述逻辑系统的方法，用逻辑系统来描述机器。所讨论的结果是指一种机器，它本质上是具有无限容量的数字计算机。它指出，有些事情是这样的机器无法做到的。如果计算机被设计成能够像在模仿游戏中那样回答问题，那么对于某些问题，无论给它多长时间，它要么给出错误的答案，要么干脆无法回答。当然存在许多这样的问题，也存在一台机器无法回答但另一台机器却能够给出满意回答的问题。我们现在假设问题只需要回答“是”或“否”，而不是像“你认为毕加索怎么样”这样的问题。我们知道机器无法回答的是这类问题：“考虑一台具有以下⋯⋯特点的机器，这台机器是否会对任何问题都给出‘是’ 的回答？”这里省略号这些点将被替换为标准形式的某种机器的描述（可能类似于第 5  节中使用的描述）。如果这里描述的“机器”与被提问的机器具有某些相对简单的联系，那么我们就能知道，要么答案是错误的，要么没有得到。这就是数学上的结论：此结论认为机器的能力是有限的，而人类的智力则没有这种限制。 [5]

对于这个论点的简短回答是，尽管可以确定的是任何特定机器的能力都存在限制，但人类的智力没有限制（这只是一个陈述，没有任何证明）。但我认为这个论点不能轻易糊弄过去。每当一台这样的机器被问及那种适当的关键问题，并给出确定的答案，而我们知道此答案一定是错误的，我们无疑会产生一种优越感，这种感觉是否是错觉？毫无疑问，这是真实的感觉，但我认为不应过分强调它。我们自己也经常会回答错误，却对机器的错误感到自鸣得意。而且，我们的优越感来自于对付一台机器， 但我们无法同时对付所有的机器而不出差错。总而言之，人类可能比任何特定的机器更聪明，但可能会有其他更聪明的机器。

我认为，坚持数学论证的人大多愿意将模仿游戏作为讨论的基础，而那些相信前两个反对意见的人可能对任何标准都不感兴趣。

6.4 来自意识的争论

关于这个论点，我引用了杰弗森（Jefferson）教授在 1949 年利斯特演讲（Lister Oration）中的一段话，他说：“如果我们要认为机器等同于大脑，那么机器就需要能够感受到思想和情绪，而不是偶然地涂写出十四行诗或协奏曲。也就是说，它不仅能做这些，还能知道自己在做什么。任何机器都无法感知到（不只是简单地发出信号）成功时的喜悦，保险丝熔断时的沮丧，被奉承时的沾沾自喜，犯错时的痛苦，性爱的享受，无法满足欲望时的愤怒或沮丧。”

这个观点看起来是否定了我们的测试方法。根据这种极端观点，一个人要确定机器是否思考，就只能成为那台机器，亲自体验思维活动。然后向其他人描述，但显然他说的没人会当真。类似地，根据这个观点，要确定某人是否在思考，唯一的方法就是成为那个人，这实际上是唯我论的观点，这或许是最有逻辑性的观点，但如果事实如此，那思想交流就会变得非常困难，A 认为“我在思考，但 B 没有在思考”，而 B 认为“我在思考，但 A 没有在思考”。与其无休止地争论这一点，不如约定每个人都在思考。

我确信杰弗森教授不愿接受那种极端和唯我论的观点。他可能会愿意接受模仿游戏作为一种测试。模仿游戏（忽略游戏者 B）通常通过“口试（viva voce）”方式来考察受试者是否是真正理解某事，而不只是鹦鹉学舌。让我们看一条这种“口试”的片段：

面试官：你的十四行诗的第一行，“我欲比君为夏日”若将“夏日”改成“春日”，是否更好？

受试者：这样就不押韵了。

面试官：改为“冬日”呢？这样会押韵。

受试者：可以，但是没有人愿意被比作冬日。

面试官：你说 Pickwick 先生 (Charles Dickens 笔下的小说人物。) 让你想到圣诞节了？

受试者：某种程度上。

面试官：然而圣诞节是冬天的一天，我认为 Pickwick 先生不会在意这个比喻。

受试者：我认为你在开玩笑，冬日是指一个典型的冬日，而不像圣诞节那样特殊的一天。⋯⋯

如果那台写十四行诗的机器在“口试”中能像这样回答，Jefferson 教授会有何看法呢？我不确定他是否会将那些机器的回答视为“人工信号”，但如果回答像上面引述的那样连贯且令人满意，我认为他不会简单地把它归因于“简单的设计”，即播放一个人念十四行诗的录音并能适时按下开关。

总的来说，我认为大多数支持来自意识方面的异议的人会被说服而放弃原先的主张，不至于堕入唯我论的困境，这样的人也可能会愿意接受我们的测试。

我不想给人一种印象，觉得我认为关于意识没有任何神秘之处。例如，存在着与定位（localise）意识有关的一些悖论，但在我们能够解答本文中探讨的问题之前，解决它们并无必要。

6.5 来自各种能力限制的争论

这些论点可以概括如下：“我确信，你可以让机器执行你提到的任何任务，但你永远也不能使一台机器具有 X 类特征。”这样的特征有很多，在这里列举一些：

善良、机智、美丽、友好、有创新精神、富有幽默感、明辨是非、会犯错误、会坠入爱河、享受草莓和奶油、会让某人爱上它、会从经验中学习、会恰当使用词汇、会成为自己思想的主人、像人一样有多样的行为、会做一些真正新颖的事情。

这些陈述通常未经证实，我相信它们大多是基于科学归纳法。一个人一生中看过成千上万的机器，由此得出一般性的结论：它们外观丑陋，应用范围狭窄，只要稍有变动要求就束手无策，行为变化微小等等。这时此人很自然地认为这是一般机器的“必备特征”。大多数机器的能力限制与机器的存储量大小有关（我假设存储量这个概念不仅仅限于离散状态的机器，还涉及到其他类型的机器，目前的讨论无须强调数学的准确性，因此定义的准确性不是很重要）。数年前，当数字计算机刚刚开始被提及时，如果你只谈论其特征而不提及其构造，人们会认为你是在信口开河。我认为这也是因为人们使用了科学归纳原则，而且很大程度上是无意识应用的结果。“一个被火烫过的小孩害怕蜡烛，于是回避蜡烛”。我认为这正是在使用科学归纳（当然，我也可以用许多其他方式来解释这一现象），但它似乎并不适用于人类的行为和习惯。如果你想要可靠的结果，就需要花费大量的人力物力进行研究，否则我们会像大多数英国儿童一样认为世界上所有的人都讲英语，学法语是一种愚蠢的行为。

关于刚才提到的机器的许多能力限制，还需要特别说几句。断言机器没有能力享受草莓和奶油，会使读者觉得有点草率。我们有可能使机器喜欢这些美味，但任何强迫这样做的企图都是愚蠢的。值得注意的是，这种能力限制对于解释其他能力限制有所帮助，比如，我们难以使人与机器之间形成像人与人之间的友好情感那样的关系。

宣称“机器不会犯错”似乎是一个奇怪的说法。人们不禁会反驳：“无法犯错会导致更糟的结果吗？”让我们站在对方的立场，来看看这（译注：“机器不会犯错”）究竟是什么意思。我认为可以用模仿游戏来解释这种批评。有人声称，在游戏中，提问者简单问几道算术题就能分辨出哪个是机器，哪个是人。由于极高的精确性，机器毫无疑问会暴露自己。对此的回复很简单，（编程用于玩模仿游戏的）机器不会试图给出算术题的正确答案，而是故意算错，以蒙骗提问者。机器也可能由于故障，在做算术题时出现错误而暴露自己。即使是对批评的这种解释，也没有充分站在对方立场上考虑，但是限于篇幅不能进一步讨论。在我看来，这种批评源于混淆了两个不同性质的错误，这两个错误我们称之为“功能错误”和“结论错误”。功能错误是由某些机械或电气故障引起的，它们导致机器不能够按照指令工作。在进行哲学讨论时，我们希望忽略发生这种错误的可能性，这样一来我们实际上是在谈论“抽象的机器”，而这些抽象的机器与其说是实在的物体，不如说是数学的虚构。从定义上讲，我们完全可以这么说：“机器从不犯错。”只有当机器的输出信号有一定的含义时才会出现结论错误。比方说，机器能够自动打出数学方程或英语句子。当机器打出一个错误的命题时，我们就认为这台机器犯了结论错误。很明显，找不到理由说机器从不犯这类错误，一台机器有可能别的什么也不能做，只会连续打出“0=1”。举一个不太反常的例子，可能有通过科学归纳得出结论的方法，但这种办法有时无疑会导致错误的结果。

有人说，机器不能成为它自己思维的主体，如果能证明机器的某些思维是有主体的话，就能驳回这种说法。尽管如此——至少对于研究它的人来说——“机器操作的主体问题”确实有一定的意义。比如，如果一台机器试图解 x2−40x−11 = 0 这个方程，我们不禁会认为，这时，这个方式本身就是机器主体的一部分。从这种意义上说，机器无疑能够成为它自己的主体。这对编排它自己的程序，对预测因自身结构变化带来的后果都会有所帮助，机器能够通过观察自己行为的结果，修改自己的程序，以便更有效地达到某种目的。这并不是乌托邦式的空想，而是不久的将来可能办到的事。

有人说，机器的行为比较单一，也就是说，机器不能够有很大的存储能力，直到最近，达到 1000 字节的存储量都很罕见。

我们这里考虑的批评，实际上都是关于意识存在异议的不同形式。通常，如果我们坚持认为，一台机器有能力做其中的一件事，并对机器所能采用的方法进行描述，这样的描述可能不会给别人留下深刻印象，人们会认为机器所使用的方法（不管是什么方法，总是机械性的）实在太低级了，参见前面所引杰弗森演讲中括号内的话。

6.6 拉芙莱斯（Lovelace）夫人的异议

有关巴贝奇分析机（Babbage’s Analytical Engine）最详细的信息来自于拉芙莱斯夫人的回忆录，她写道：“分析机没有创造任何东西的野心。对于任何事情，只要我们知道如何指挥它，它就可以执行。”（回忆录原文中使用斜体），哈特里（Hartree）引用了这段话（第 70 页），并补充道：“这并不意味着就无法制造能够‘独立思考’的电子设备，用生物学的术语来说，我们可以在其中建立条件反射， 用来构建‘学习’的基础。这一设想在原则上是否可行，是一个令人兴奋的话题，但当时制造的机器似乎还没有这个特性。

我完全同意哈特里的观点，值得注意的是，他并没有断言当时的机器不具备这个特性，而是指出拉芙莱斯夫人能获得的证据还不足以使她相信这些机器已经具备了这个特性。从某种意义上说，这些机器很有可能已经具备了这个特性，因为我们设想某些离散状态机具有这个特性，分析机实际上是一台通用数字计算机，因此如果它的存储能力和速度达到一定程度，就能通过适当的编程模仿我们所讨论的机器，也许伯爵夫人或巴贝奇（Babbage）并没有考虑到这一点。不管怎样，他们并没有义务陈述一切可以陈述的事情。

整个问题将在学习机器（Learning Machines）的标题下再次考虑。

拉芙莱斯夫人的异议还有另一种说法，即机器“永远不能创新”，这种说法可以用谚语“太阳底下无新事” (There is nothing new under the sun) 来暂时支撑。谁能保证，他的“独创性工作”不是通过教育让身上的种子成长的结果，或者不是因循著名的普遍原则的结果？此异议还有另一个稍好的说法，即机器永远也不能“让我们吃惊”，这种说法是一个更直截了当的挑战，但也可以回应：机器经常令我吃惊，这主要是由于我对机器能做什么估计不足，更确切地说是由于即使我做了估计，也是很草率的。我也许这样对自己说：“我认为这里的电势应与那里相同：不管怎样，就假设一样吧。”自然我经常出错，结果我大吃一惊，一旦实验完成，这些假设就被忘得一干二净。我承认自己的错误，但请读者不要因此对我所经历的这些令我吃惊的事产生怀疑。

我的回答可能并不会使批评者就此缄口沉默，他也许会说，所谓吃惊都是因为我自己富于想象的心理活动，与机器本身毫不相干。这导致我们又回到意识的争论上，而背离了吃惊不吃惊的话题。因此我们不得不认为这是循环论证，但也许值得一提的是，要将某事物认作令人吃惊，的确需要许多“富于想象力的心理活动”，不管这件令人吃惊的事件是由一个人、一本书、一台机器还是其他任何东西引起的。

我相信，那种认为机器不会令人吃惊的观点，是哲学家和数学家特别关注的一个谬误。它是一个这样的假设：心灵一接受了某个事实，由此事实所引起的一切后果都会同时涌入心灵。在许多情况下，这种假设十分有用，但人们太容易忘了这是个错误的假设。如果这么做的话，其必然结果就是认为，仅仅从数据和普遍原则推出的结果会毫无价值。

6.7 来自神经系统连续性的争论

神经系统显然不是离散状态机，神经元激活的脉冲幅度的信息存在的小误差，可能导致输出脉冲幅度的信息相差甚远。由此可能有人认为：使用离散状态系统无法模拟神经系统的行为。

虽然离散状态机与连续机器有所不同，但如果我们遵守模仿游戏的规则，提问者将无法利用这种差异。对于其他一些更简单的连续机器，情况更加清晰：一台微分分析机（微分分析机是一种非离散状态的用于计算的机器）已足以胜任，一些机器能够打字输出答案，因此可以参与模仿游戏。数字计算机不可能准确预测微分分析机对问题的回答，但它（译注：微分分析机）却完全能给出正确的回答。例如，如果要求其回答 π 的值是多少（实际上约等于 3.1416），它会在 3.12、3.13、3.14、3.15、3.16之间随机选择，选择概率可以是 0.05、0.15、0.55、0.19、0.06。这使得提问者很难区分它们。

6.8 来自行为非形式化的争论

机器不可能制定一套旨在描述在每种情况下该采取何种行动的规则，例如可能有这样一条规则：红灯停，绿灯行，但是，如果由于某种错误红绿灯同时亮了，该怎么办？我们可能会决定，为了安全起见最好停止，但这个决定还会引发其他问题。试图提出一套考虑到各种可能性的行为规则，即使是如红绿灯这样的规则，似乎都是不可能的。我完全同意这一观点。

由此有人认为我们不能成为机器。我会尽力重现这一论证，但我担心很难做到公正。似乎可以这么说：“如果每个人都有一套行动规则来调控其生活，那么他与机器就相差无几了。但不存在这样的规则，因此人不能成为机器”。这里的中项不周延[6]很明显，我认为没人这样论证过，但实际上就是这样。然而，“行为规则”和“行为规律”之间可能存在一定的混淆，所谓“行为准则”，我是指诸如“红灯 停”这样的规则，你能采取行动，并意识到；而所谓“行为规律”则是指适用于人体的自然法则，例如“如果你捏他，他就会叫”。如果我们在上述论证中用“规范他的生活的行为规律”来替代“规定他的生活的行为规则”，那么这个论证中的不周延的中项就不再是不可克服的了。因为我们认为，受行为规律调控意味着人就是某种机器（尽管不一定是离散状态机），而且反过来说，这样的机器意味着受这样规律调控。然而，我们很难轻易地说服自己，不存在完备行为规律，就像不存在完备行为规则一样。我们知道，找到这些规律的唯一方法是科学观察，而在任何情况下都不能说“我们已充分寻找过了，不存在这样的规律。”

我们可以更有力地证明这种说法不合理。假定我们确信，如果存在这种规律，则我们肯定能够找到。然后给定一个离散状态机，应该有可能通过观察找到规律，在合理的时间内（比如 1000 年）预测其未来行为，但事实似乎并非如此。我在曼彻斯特电脑上安装了一个只占 1000 个存储单元的小程序，机器给定一个十六进制输入可以在两秒钟内给出对应的十六进制输出。我绝对不相信任何人仅从这些回答中就能充分了解这个程序，能对未来的输入值做出准确的预测。

6.9 来自超感官知觉的争议

我假设读者对超感官知觉（extra-sensory perception）有所了解，这包括心灵感应（telepathy）、遥视（clairvoyance）、预知未来（precognition）和意念移物（psycho-kinesis）。这些现象似乎与一般科学观念相悖，有些令人不安，我们很想对这些提出质疑，但统计证据至少支持了心灵感应。人们难以改变自己的观念来接受这些新事物，接受了这些现象，仿佛就距离相信鬼怪不远了。进入这一领域的第一步，是相信我们的身体可能遵循未知但相似于已知物理学规律的规则。

在我看来，这是一个强有力的论点。有人可能会说，许多科学理论实践上仍然有效，尽管与超感知觉相冲突；事实上，即使忽略这些现象，人们也可以生活得很好。这种说法有点冷漠，因为人们害怕思维与超感官知觉之间可能存在特殊联系。

基于超感官知觉的更具体论证大致如下：“让我们再来玩模仿游戏：让一个擅长心灵感应的人和一台数字计算机参赛。提问者问道：“我右手的牌是什么花色？”这样的问题。能心灵感应或遥视的人可以在 400 张牌中答对 130 张，而机器只能随机猜测，可能只能答对 104 张，提问者就可以做出正确的判断。”这里开启了一个有趣的可能性。如果这台数字计算机有一个随机数字生成程序，那么我们会用这个程序来决定答案。但这个随机数字生成程序也会受到提问者心理活动的影响，这种影响可能会让计算机的答对次数高于概率预测，这时提问者就无法做出正确判断。另一方面，提问者也可能通过遥视而不用提问就猜对。超感官知觉的介入会带来各种可能性。

如果允许心灵感应参与模仿游戏，我们就需要严格规定测试方式。这就好比在模仿游戏中，被询问的对象则贴着墙偷听提问者的自言自语。假如将受试者置于一间“防心灵感应室”，那就能满足所有要求。

7. 学习机器

读者可能会猜测我缺乏令人信服的正面论据来支持我的观点，否则我不会花费那么多精力来指出异议中的问题。现在我将提供这样的证据。

让我们暂时回到拉芙莱斯夫人的异议，她认为机器只能执行我们告诉它的任务，可以说，人类向机器“注入”一个念头，机器在某种程度上作出反应，最后又回到静止，就像被琴槌敲击的钢琴弦一样。另一个比喻是一个低于临界体积的反应堆：注入的念头就像从外部轰击反应堆的中子，每个中子会引起一些反应，但最终逐渐消失。然而，如果反应堆足够大，中子引起的反应可能会持续增加，直到反应堆解体。思维中是否存在这种现象？在机器中呢？这种现‍‍象在人脑中应该存在。绝大多数思想都处于“亚临界”状态，对应于亚临界体积的反应堆，一个思想进入这样的状态，平均下来只会产生少于一个的思想。有一小部分思想处于超临界状态，进入其中的思想将会产生二级、三级……越来越多的思想，最终形成一个完整的“理论”。动物的大脑似乎是处于亚临界状态。由于这种相似性，我们不得不问：“机器能否达到超临界状态？” (Can a machine be made super-critical?)

“洋葱皮”的类比也有用。在研究思维或大脑功能时，我们发现一些操作完全可以用纯“物理”的方式解释，我们说这并不符合真正的思维。但在剩下的部分里，我们发现还有“洋葱皮”需要剥去，一直这样下去。用这种方式，我们是否能够达到真正的“智能”，或者最终发现皮里面什么也没有了？如果是后一种情况，那么整个思维都是机械的。（但它不是一个离散状态机，我们已经做了说明）

上述两段并没有提供令人信服的论据，倒不如称作“趋于产生信念的陈述”（recitations tending to produce belief）。

要在第六部分开始时提出的观点得到真正令人满意的支持，只能等到本世纪末再进行所描述的实验了。但是在此期间，我们可以说些什么呢？如果实验将来会成功，我们现在应该采取什么步骤？

正如我所解释，问题主要在于编程。工程上的进步也是必要的，但似乎无法满足所需。人们估计大脑的存储能力在 1010 到 1015 之间，我倾向于取下界，认为只有一小部分用于进行高级思考，其余大部分用于保存图像。在模仿游戏中应对一个盲人，如果所需的存储量超过 109，会让我感到惊讶（注：大英百科全书第 11 版中的脑容量为 2 × 109），即使采用现有技术，107 的存储量也是完全可行的，也许不需要提高机器的运行速度。被视为模拟神经细胞的现代机器速度比神经细胞快 1000 倍，在许多方面提供了“安全余地”，剩下的问题主要是如何编程让机器能够完成游戏。按照我目前的工作速度，我一天大概能编写 1000 字节的程序，所以大约需要 60 个工人连续稳定工作 50 年，而且没有东西扔进废纸篓，才能完成这项工作，但似乎需要一些更快捷的方法。

在试图模拟成人大脑的过程中，我们必须考虑大脑是如何变成我们现在这样的。我们考虑其中的三个部分：

• 心智的初始状态，即出生时的状态。
• 其所接受的教育。

• 其所接受的其他的、不被称为教育的经验。

与其试图编程模拟成人大脑，不如模拟儿童大脑（Instead of trying to produce a programme to simulate the adult mind, why not rather try to produce one which simulates a child’s?），如果让儿童大脑接受正确的教育课程，就可能获得成人大脑。儿童大脑大概就像一个刚从文具店买来的笔记本，只有少许机制和大段空白的纸张（机制和写字在我们看来几乎同义)，我们希望儿童大脑中的机制足够少使得容易编程。我们可以假设对机器进行教育的工作量和教育一个人类儿童基本相当。

因此，我们把问题分为密切相关的两个部分：儿童程序和教育过程。我们不能指望一下子找到一个好的“儿童机器”，我们必须做对这样的机器进行教育的实验，看其学习效果，然后再试另一个，判断哪个更好。显然这个过程与进化有联系，通过这样的类比：

儿童机器的结构 = 遗传物质

儿童机器的变化 = 变异

试验者的决定的判断 = 自然选择

然而，有人可能期望这一过程比自然进化更加迅速，优胜劣汰虽然是一种缓慢的方式，但实验者通过运用其智力将促使这一进程的加速。同等重要的是，这并非局限于随机的变异，只要能找出某些缺陷的根本原因，就有可能考虑对其进行改进。

机器无法采用与儿童完全相同的教育方法，例如，它没有腿，因此不能要求它出去填煤斗；或许它也没有眼睛。然而，无论聪明的工程师采用何种手段克服这些缺陷，只要这样的机器进入人类学校，其他学生肯定会嘲笑它。它必须接受培训。另外我们不能过于关注腿、眼睛等“缺陷”，海伦·凯勒（Helen Keller）女士的例子表明只要教师和学生能够以某种方式进行有效交流，教育仍然可以取得成功。

通常，我们将教育过程与惩戒和奖励紧密联系起来。一些基于简单原则构建或编程的儿童机器可以降低受到惩罚事件的发生频率，同时增加受到奖励事件的发生频率。这些定义并不预设机器有任何感觉。我对这样一个儿童机器进行了一些实验，并成功地教会了它一些东西，但教学方法过于非正统，所以这个实验不能被认为真正成功。

使用奖励和惩罚的做法最好只是教学过程的一方面。总体来说，如果教师没有其他与学生沟通的方式，所传递的信息量就不会超过所使用奖励和惩罚的总和。当学生只能通过“二十问”的方式反复学习“Casabianca”这个词时，会感到相当痛苦，每个“错！”都是一种打击。因此，我们还需要采用其他“非情感”的沟通方式，这样，通过奖励和惩罚，机器就能服从于以某种符号语言给出的命令，而这些命令通过“非情感”的途径传达，这种语言的使用将大大减少需要奖励和惩罚的次数。

对于构建适用于儿童机器的复杂度，人们可能有不同的看法。有人主张尽量保持简单、服从一般的原理。有人主张嵌入一个完整的逻辑推理系统[7]。在后者的情况下，大部分存储空间将用于存储定义和命题，这些命题可能具有各种形式，比如确定的事实、推测、数学上证明的定理、权威的判断，以及具有逻辑形式但没有确定值的表达式等等。一些命题可以被称为“命令句（imperatives）”，即机器应该在命令确定时立即自动执行适当的动作。例如，如果老师告诉机器“现在做你的家庭作业”，这将使“老师说‘现在做你的作业’”成为确定的事实；另一个事实可能是“老师说的一切都是对的”。这两者结合在一起将使“现在做家庭作业”成为确定的事实。根据机器的构造规则，这意味着立即开始做作业，这种效果还是令人满意的。机器的推理过程并不需要像严格的逻辑家所做的那样，可能没有类型的层次结构，但这并不意味着发生类型错误的几率会比我们从悬崖上跌落的几率高。合理的命令（在系统内部表达，而不是系统规则的一部分，比如“不要使用一个类，除非它是老师提到的类的一个子类”）与“不要让他靠近悬崖边缘”具有相似的效果。

机器人没有肢体的情况下执行的指令必然是具有智力的，正如前文（做作业）例子所述。在这些指令中，最为关键的是调整逻辑系统规则的执行顺序。在使用这个系统的每一步中，都存在着众多不同的选择，只要遵守逻辑系统规则，就可以任意选择其中之一。这些选择决定了推理者是出色还是平庸，而不是决定了推理是正确还是谬误的。这些指令可能涉及命题，比如“提到苏格拉底（Socrates）时，采用巴巴拉（Babara）的三段论”或“如果有一种方法被证明比另一种方法更快，那就不要使用慢的方法。”这些命题可以来自权威，也可以来自机器本身，比如科学归纳法。

学习机器的概念对一些读者来说可能显得有些矛盾。机器的操作规则怎么可能改变呢？无论机器经历过什么，未来会发生什么变化，其操作规则都应该完整地描述机器的反应方式，即这些规则是不会随时间变化的。确实，解释这个悖论的方法是，在学习过程中发生变化的是那种相对不那么“自负的（pretentious）”规则，它们的有效性很短暂。读者可以将其与美国宪法进行类比。

学习机器的一个重要特征是，通常老师对机器内部发生的事情一无所知，尽管老师仍然可以在一定程度上预测学生的行为。经过实验和精心设计（或编程）的儿童机器的后期教育尤其如此。这与进行正常计算的机器形成了鲜明对比：在那里，我们的目标是清晰地了解机器在计算中的状态，而要达到这个目标需要付出艰苦的努力。因此，“机器只能做我们知道如何命令它做的事”[8]的观点就显得奇怪了，因为输入机器的大多数程序最终会执行一些我们无法理解或认为是完全随机的行为。智能行为应该与完全服从命令的行为有所区别，但也不能太过自由，不应该导致随机行为或毫无意义的重复循环。通过教育和学习，我们的机器能够进行模仿游戏的一个重要结果是，“人类的易错性”可能会被相当自然地忽略，即不需要特定的“指导”（读者应该将其与第 454 页上的观点放在一起看）。学习的过程并不会产生百分之百的确定结果，否则就无法被修改或遗忘。

在学习机器中引入随机元素是明智之举（见第 445 页）。在寻找某个问题的解时，随机元素非常有用。例如，我们要找到一个介于 50 和 200 之间的数，它等于其各个位置数字的和的平方。我们可以从 51，52 开始，一直尝试下去直到找到满足条件的数。另一种方法是随机选择数字，直到找到满足条件的数。这种方法的优点是不需要追踪已经尝试过的值，但缺点是一个数可能会被多次选中，但如果 存在多个满足条件的数，这点就不太重要了。系统方法的一个缺点是可能有一段范围内不存在解，但我们需要先进行判断。现在的学习过程可以看作是寻找满足老师要求（或其他标准）的行为，因为可能存在大量的满足要求的解，随机性方法可能比系统性的方法更为有效。值得注意的是，在进化过程中也采用了类似的方法，因为在那里系统性的方法是不切实际的：如何追踪已经尝试过的不同基因组合，以避免重复呢？

我们希望机器最终能在所有纯智力领域与人类竞争，但最好的起点在哪里？即使是这个决定也是困难的。许多人认为抽象的活动，如国际象棋，可能是最佳选择；还有人认为最好的方法是花钱购买最先进的传感器，然后教机器听、说英语，就像教正常的孩子一样，教它命名事物等等。我不知道正确的答案，但我认为两者都值得一试。

我们的目光所及，只是不远的前方，但是可以看到，还有许多工作要做。

注释

[1]译注：Forth Bridge, 1890 建成于英国，开现代桥梁建造的先河

[2]译注：这句话的翻译源自文章“图灵测试是人工智能的标准吗？”（作者：王培）。原文是：May not machines carry out something which ought to be described as thinking but which is very different from what a man does? This objection is a very strong one, but at least we can say that if, nevertheless, a machine can be constructed to play the imitation game satisfactorily, we need not be troubled by this objection.

[3]译注：这样就不可能通过自然生产的方式得到一个人类个体.

[4]译注：离散状态机也可以采用状态转移图的方式进行更加直观的表示，其中圆圈表示状态，箭头表示状态之间的转移：

[5]译注：这段中图灵说得不太清楚，但大概谈的是“停机问题”。

[6]译注：中项不周延是指三段论中的中项，在大、小前提中一次也不周延以致无法必然推出结论的错误逻辑。例如：从“一切液体都有弹性，这种物体有弹性”这两个前提出发，无法推出“这种物体是（或不是）液体”的结论。

[7]作者注：或者更确切地说，我们的儿童机器的“编程”将在数字计算机中进行，但逻辑系统不需要通过学习得到。(Orrather ’programmed in’ for our child-machine will be programmed in s digital computer. But the logical system will not have to be learnt.)

[8]作者注：注意这里和 Lovelace 的观点不同后者并没有“只能”这两个字。(Compare to Lady Lovelace’s statement, which does not contain the word ’only’.)

参考文献

1.Samuel Butler, Erewhon, London, 1865. Chapters 23, 24, 25, The Book of the Machines.

2.Alonzo Church, An Unsolvable Problem of Elementary Number Theory”, American J. of Math., 58(1936), 345–363.

3.K. Gödel, Über formal unentscheildbare Sätze der Principia Mathematica und verwandter Sys- teme, I”, Monatshefle für Math. und Phys. , (1931), 173–189.

4.D. R. Hartree, Calculating Instruments and Machines, New York, 1949.

5.S. C. Kleene, General Recursive Functions of Natural Numbers ”, American J. of Math., 57(1935), 153–173 and 219–244.

6.G. Jefferson, The Mind of Mechanical Man”. Lister Oration for 1949. British Medical Journal, vol.i (1949), 1105–1121.

7.Countess of Lovelace, Translator’s notes te an article on Babbage’s Analytical Engire”, Scientific Memoirs (ed. by R. Taylor), vol.3 (1842), 691–731.

8.Bertrand Russell, History of Western Philosophy, London, 1940.

9.A. M. Turing, On Computable Numbers, with an Application to the Entscheidungsproblem”,Proc.London Math.Soc. (2), 42 (1937), 230–265. Victoria University of Manchester.

本文在翻译过程中部分参考了网上已有的这篇翻译资料，特此说明：

https://blog.csdn.net/LSG_Down/article/details/84544547

AGI读书会

为了深入探讨 AGI 相关话题，集智俱乐部联合集萃深度感知技术研究所所长岳玉涛、麻省理工学院博士沈马成、天普大学博士生徐博文，共同发起 AGI 读书会，涵盖主题包括：智能的定义与度量、智能的原理、大语言模型与信息世界的智能、感知与具身智能、多视角下的人工智能、对齐技术与AGI安全性、AGI时代的未来社会。欢迎感兴趣的朋友报名参与！

详情请见：

AGI 读书会启动：迈向通用人工智能的跨学科路径

“后ChatGPT”读书会

2022年11月30日，一个现象级应用程序诞生于互联网，这就是OpenAI开发的ChatGPT。从问答到写程序，从提取摘要到论文写作，ChatGPT展现出了多样化的通用智能。于是，微软、谷歌、百度、阿里、讯飞，互联网大佬们纷纷摩拳擦掌准备入场……但是，请先冷静一下…… 现在 all in 大语言模型是否真的合适？要知道，ChatGPT的背后其实就是深度学习+大数据+大模型，而这些要素早在5年前的AlphaGo时期就已经开始火热了。5年前没有抓住机遇，现在又凭什么可以搭上大语言模型这趟列车呢？
集智俱乐部特别组织“后 ChatGPT”读书会，由北师大教授、集智俱乐部创始人张江老师联合肖达、李嫣然、崔鹏、侯月源、钟翰廷、卢燚等多位老师共同发起，旨在系统性地梳理ChatGPT技术，并发现其弱点与短板。

详情请见：
“后 ChatGPT”读书会启动：从通用人工智能到意识机器

推荐阅读

1. 让 ChatGPT 拥有意识，冯·诺依曼会怎么做？——自指机器的奥秘2. “意识机器”初探：如何让大语言模型具备自我意识？3. 通用人工智能（AGI）已经到来？深度解析 ChatGPT 获得智能的数学物理机理4. 机器意识：人工智能的终极挑战5. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程6. 成为集智VIP，解锁全站课程／读书会7. 加入集智，一起复杂！

点击“阅读原文”，报名读书会