PRL速递：高阶时序网络的渗流与拓扑

关键词：高阶网络，隐藏变量框架，渗流，拓扑

论文题目：Percolation and Topological Properties of Temporal Higher-Order Networks论文期刊：Physical Review Letters论文地址：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.037401‍

网络科学常通过节点和边的关系图来描述系统中的交互关系。传统的网络模型在描述涉及复杂系统中的非成对交互时存在局限，如科学家合作网络、复杂生化反应系统、脑网络等。为了更准确地捕捉这些系统的结构和动力学行为，研究者们将目光投向了高阶网络模型。

隐藏变量框架（hidden variable framework, HV）理论是统计建模的有力工具，已被广泛应用于一阶生成过程，如将网络映射到嵌入空间；HV形式理论在普通网络中的应用已经取得了显著的成果，已被应用在存在结构相关性的网络、时变网络、存在内在相关性的网络等等。这一框架通过引入未观测的变量，可以更好地解释模型中的复杂结构和潜在关系。然而，对于高阶网络的研究，尤其是高阶活动驱动模型（higher-order activity-driven model，HOAD），隐藏变量框架的应用还相对较少。

最近发表在Physical Review Letters的这篇文章提出将隐藏变量框架应用于高阶活动驱动模型。在传统的网络模型中，活动往往指的是节点之间的两两交互。而在高阶活动驱动模型中，不仅考虑了节点间的成对交互，还考虑了多个节点之间的高阶交互，即超图的结构。 他们研究了系统的连通特性，并得到了极限条件下的解析表达式。此外，研究者还提供了关于高阶系统中渗流时间的估计。

这项研究为我们提供了一种全新的视角，来理解复杂系统中高阶交互的动态演化。通过将隐藏变量框架引入高阶活动驱动模型，我们能够更准确地建模系统的结构，揭示出隐藏在复杂网络背后的潜在规律。这不仅对网络科学领域具有推动作用，还在社交网络、药物设计、生物学等领域显示出广泛的应用前景。通过对高阶活动驱动网络的深入理解，我们可以更好地预测系统的动态行为，为未来的网络科学研究和实际应用提供新的方法和思路。

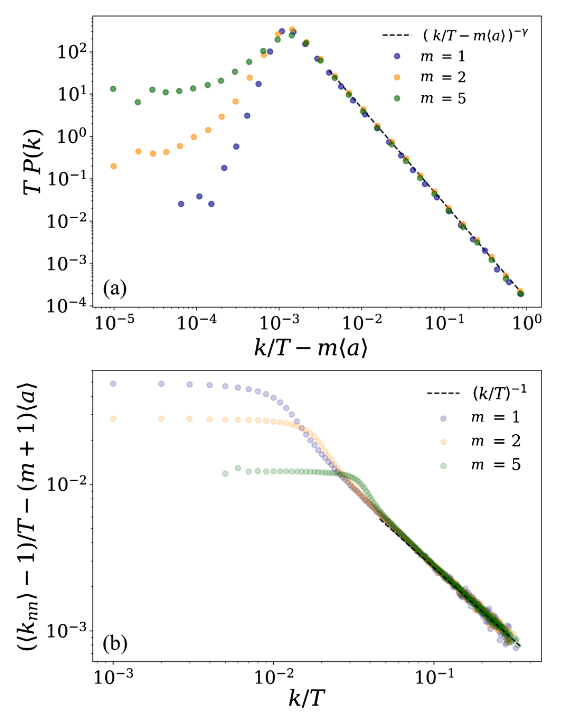
图1 高阶活动驱动网络模型（HOAD）的拓扑性质。a）超度（Hyperdegree）分布；b）超度（Hyperdegree）相关性。虚线为文章给出的解析结果。

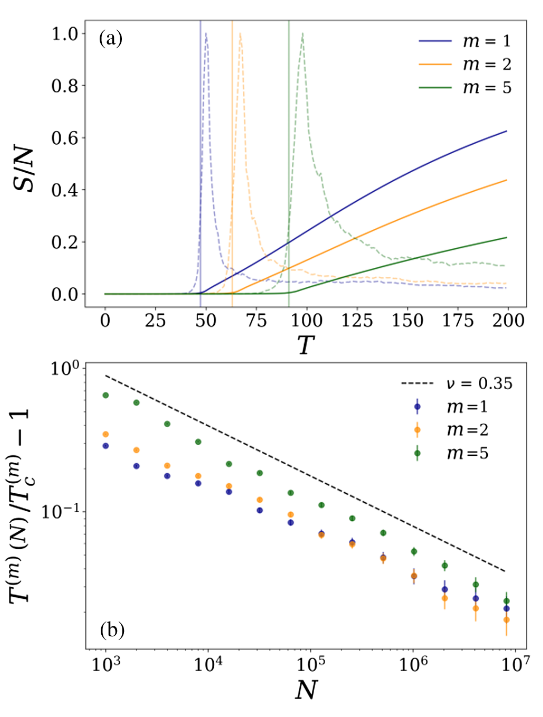
图2 高阶活动驱动网络模型（HOAD）的渗流时间。a）巨分量大小S/N（实线）及其方差的峰值（虚线）随时间变化的结果。b）有限尺度的相对差异分析。

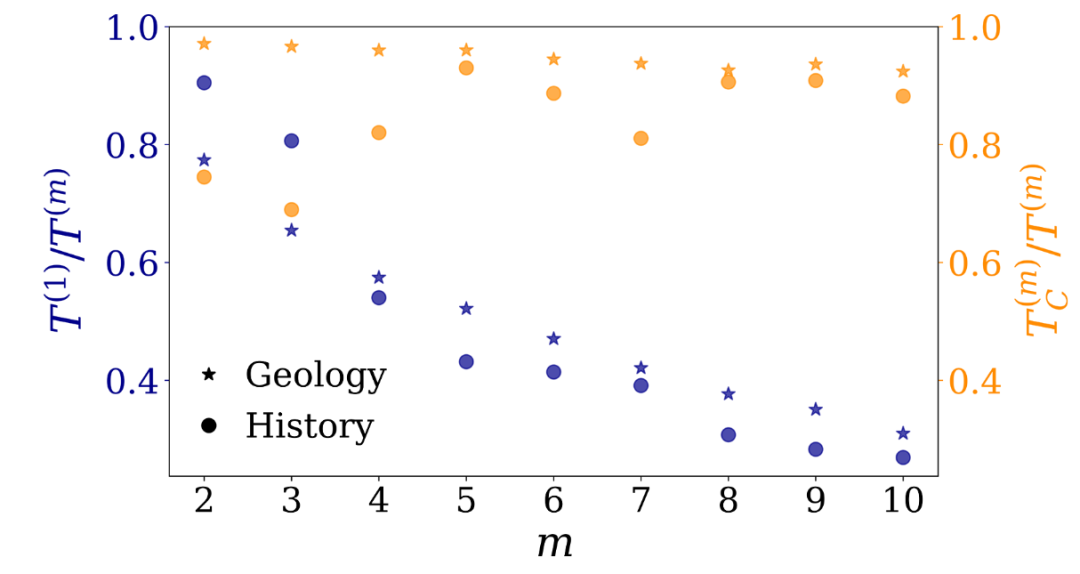
图3 实证数据中的渗流时间。地理学科学合作网络（星形）和历史学科学合作网络（圆点）。蓝色点（左y轴）：实证数据中一阶渗流时间与m阶渗流时间之比；黄色点（右y轴）：m阶渗流时间的理论预测与实证数据之比。

编译｜朱欣怡

高阶网络社区

详情请见：

探索复杂系统高阶交互的奥秘 | 高阶网络读书会启动

‍推荐阅读1. Bianconi 新作：超图上的渗流理论2. 玛丽女王大学 Ginestra Bianconi：高阶网络的拓扑结构与动力学3. 前沿速递：集群时间序列变点检测的高阶拓扑特征提取4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 加入集智学园VIP，一次性获取集智平台所有内容资源6. 加入集智，一起复杂！

点击“阅读原文”，报名读书会