这篇文章将介绍有关在 Transformer架构和大型语言模型(LLMs)中使用的自注意力机制,例如GPT-4和Llama。自注意力和相关机制是LLMs的核心组件,因此在使用这些模型时理解它们是很有用的主题。
然而,与其仅仅讨论自注意力机制,我们将从头开始使用Python和PyTorch对其进行编码。在我看来,从零开始编写算法、模型和技术是学习的一种极好方式!
以下是说明自注意力机制如何融入语言模型整体框架的思维模型。
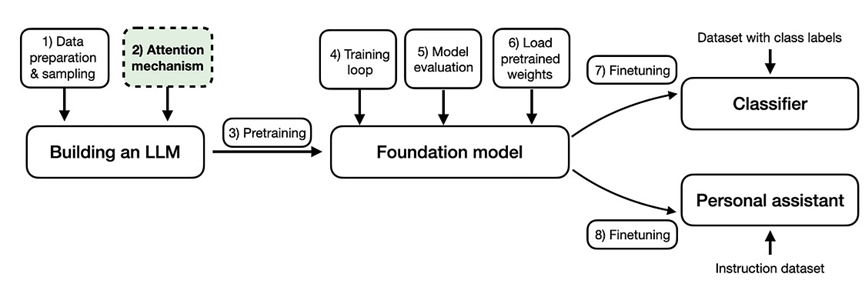
从零开始构建大型语言模型
为了保持本文篇幅较为合理,我将假设你已经对大型语言模型(LLMs)和注意力机制有基本了解。本文的目标和重点是通过Python和PyTorch的代码演示来理解注意力机制的工作原理。
介绍自注意力
自注意力机制自从通过原始 Transformer论文《Attention Is All You Need》引入以来,已经成为许多最先进的深度学习模型的基石,特别是在自然语言处理(NLP)领域。由于自注意力现在无处不在,理解它的工作原理变得至关重要。
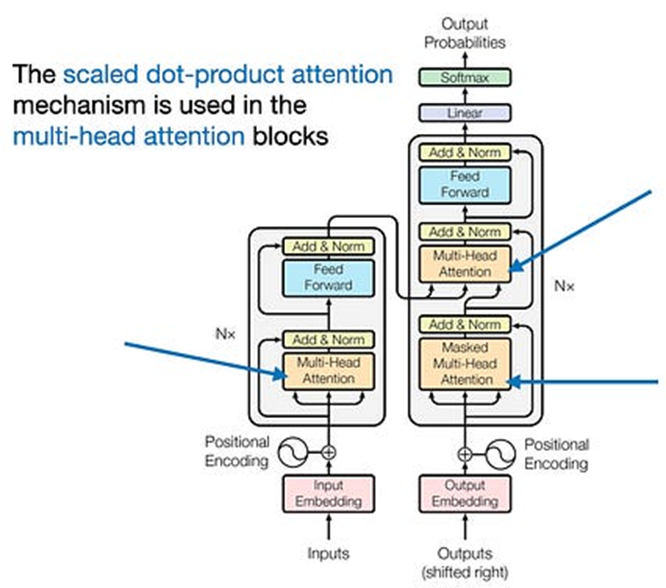
https://arxiv.org/abs/1706.03762上的原始 Transformer架构
深度学习中的“注意力”概念起源于改进递归神经网络(RNNs)以处理更长的序列或句子的努力。例如,考虑将一种语言的句子翻译成另一种语言。通常无法逐字逐句地翻译一句话,因为这会忽略每种语言独特的复杂语法结构和习惯用语表达,导致翻译不准确或毫无意义。
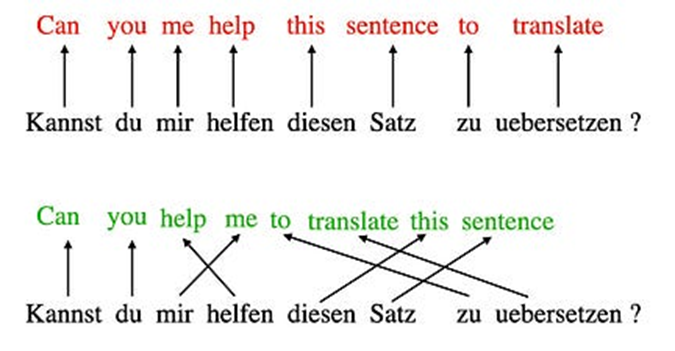
一个逐字逐句的错误翻译(顶部)与正确翻译(底部)的比较
为了克服这个问题,引入了注意力机制,使得在每个时间步都能访问所有序列元素。关键在于选择性地确定在特定上下文中哪些单词最重要。在2017年,Transformer架构引入了独立的自注意力机制,完全消除了对RNN的需求。
(为了简洁起见,并使文章专注于技术自注意力细节,我将保持这个背景动机部分简短,以便我们可以专注于代码实现。)
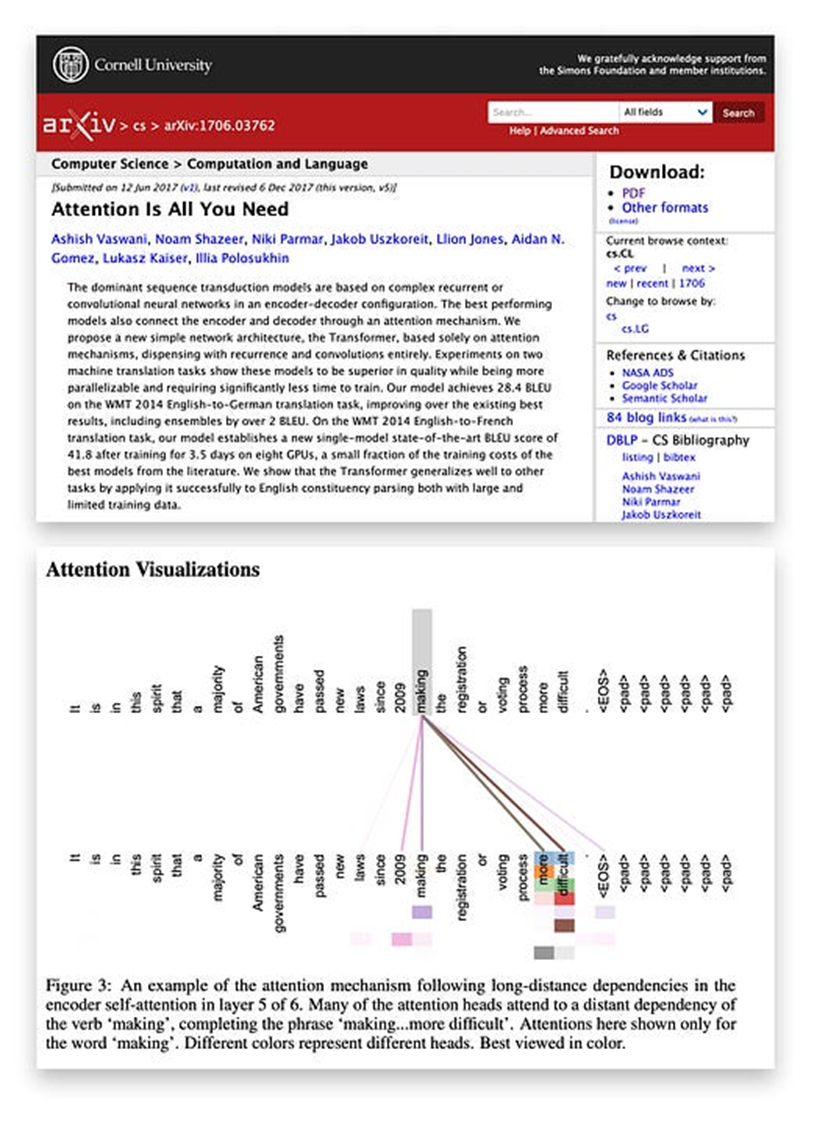
在《Attention is All You Need》论文(https://arxiv.org/abs/1706.03762)中的可视化展示了单词“making”通过注意力权重在输入中依赖或聚焦于其他单词(颜色强度与注意力权重值成比例)
我们可以将自注意力视为一种机制,通过包含有关输入上下文的信息来增强输入嵌入的信息内容。换句话说,自注意力机制使模型能够权衡输入序列中不同元素的重要性,并动态调整它们对输出的影响。这在语言处理任务中尤为重要,因为一个词在句子或文档中的上下文中其含义可能会改变。
请注意,有许多变体的自注意力。特别关注的是使自注意力更加高效。然而,由于自注意力很少是大多数公司训练大规模 Transformer的计算瓶颈,大多数论文仍然实现了《Attention is All You Need》论文中引入的原始缩放点积注意力机制。
因此,在本文中,我们专注于原始的缩放点积注意力机制(称为自注意力),它仍然是实践中最受欢迎和广泛使用的注意力机制。然而,如果你对其他类型的注意力机制感兴趣,请查阅2020年的《高效Transformer:一项调查》、2023年的《 Transformer高效训练调查》以及最近的FlashAttention和FlashAttention-v2论文。
嵌入输入句子
在开始之前,让我们考虑一个输入句子“Life is short, eat dessert first”,我们希望通过自注意力机制处理它。与处理文本的其他建模方法(例如使用递归神经网络或卷积神经网络)类似,我们首先创建一个句子嵌入。
为简单起见,这里我们的字典 dc 仅限于出现在输入句子中的单词。在实际应用中,我们将考虑训练数据集中的所有单词(典型的词汇量大小在30,000到50,000个条目之间)。
In:
sentence = ‘Life is short, eat dessert
first’dc = {s:i for i,sin enumerate(sorted(sentence.replace(‘,’, ”).split()))}
print(dc)
Out:
{‘Life’: 0, ‘dessert’: 1, ‘eat’: 2, ‘first’: 3, ‘is’: 4,
‘short’: 5}
接下来,我们使用这个字典为每个单词分配一个整数索引:
In:
import torch
sentence_int = torch.tensor(
[dc[s] for s in sentence.replace(‘,’, ”).split()]
)
print(sentence_int)
Out:
tensor([0, 4, 5, 2, 1, 3])
现在,使用输入句子的整数向量表示,我们可以使用嵌入层将输入编码成实向量嵌入。在这里,我们将使用一个微小的3维嵌入,以便每个输入单词由一个3维向量表示。
请注意,嵌入大小通常范围从几百到几千维。例如,Llama 2 利用了4,096的嵌入大小。我们在这里使用3维嵌入的原因纯粹是为了说明。这样我们可以检查每个向量,而不是在整个页面上填满数字。
由于句子由6个单词组成,这将导致一个6×3维的嵌入:
In:
vocab_size = 50_000
torch.manual_seed(123)
embed = torch.nn.Embedding(vocab_size, 3)
embedded_sentence = embed(sentence_int).detach()
print(embedded_sentence)
print(embedded_sentence.shape)
Out:
tensor([[ 0.3374, -0.1778, -0.3035],
[ 0.1794, 1.8951, 0.4954],
[ 0.2692, -0.0770, -1.0205],
[-0.2196, -0.3792, 0.7671],
[-0.5880, 0.3486, 0.6603],
[-1.1925, 0.6984, -1.4097]])
torch.Size([6, 3])
定义权重矩阵
现在,让我们讨论被广泛使用的自注意力机制,即缩放点积注意力,它是 Transformer架构的一个组成部分。
自注意力机制使用三个权重矩阵,分别称为W_q、W_k和W_v,这些矩阵在训练过程中作为模型参数进行调整。这些矩阵用于将输入投影到序列的查询、键和值组件中。
通过权重矩阵W和嵌入输入x之间的矩阵乘法,得到相应的查询、键和值序列:
·Query sequence: q(i) = W_q x(i) for i in
sequence 1 … T
·Key sequence: k(i) = W_k x(i) for i in
sequence 1 … T
·Value sequence: v(i) = W_v x(i) for i in
sequence 1 … T
索引 i 指的是输入序列中的令牌索引位置,其长度为 T。
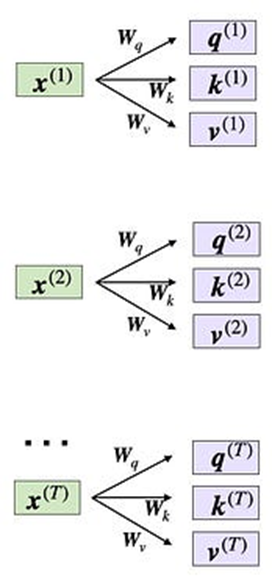
通过输入 x 和权重矩阵 W 计算查询、键和值向量
在这里,q(i) 和 k(i) 都是维度为d_k 的向量。投影矩阵 W_q 和 W_k 的形状为 d_k × d,而 W_v 的形状为d_v × d。
(重要说明:d 表示每个单词向量 x 的大小。)
由于我们正在计算查询和键向量之间的点积,这两个向量必须包含相同数量的元素(d_q = d_k)。在许多大型语言模型中,我们使用相同大小的值向量,使得 d_q =
d_k = d_v。然而,决定结果上下文向量大小的值向量 v(i) 中的元素数量可以是任意的。
因此,在接下来的代码演示中,我们将设置 d_q = d_k = 2,并使用 d_v = 4,初始化投影矩阵如下:
In:
torch.manual_seed(123)
d = embedded_sentence.shape[1]
d_q, d_k, d_v = 2, 2, 4
W_query = torch.nn.Parameter(torch.rand(d_q, d))
W_key = torch.nn.Parameter(torch.rand(d_k, d))
W_value = torch.nn.Parameter(torch.rand(d_v, d))
(与先前的单词嵌入向量类似,维度 d_q、d_k、d_v 通常要大得多,但我们在这里使用小的数字仅用于说明目的。)
计算未归一化的注意力权重
现在,假设我们有兴趣计算第二个输入元素的注意力向量——第二个输入元素在这里充当查询:
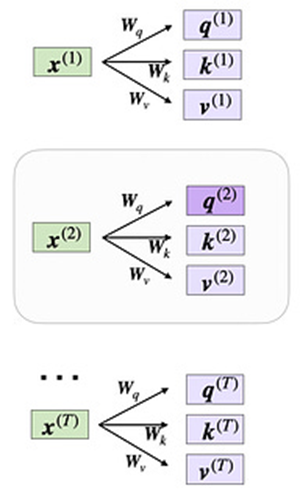
在接下来的部分中,我们将专注于第二个输入 x(2)
在代码中,这看起来如下:
In:
x_2 = embedded_sentence[1]
query_2 = W_query @ x_2
key_2 = W_key @ x_2
value_2 = W_value @ x_2
print(query_2.shape)
print(key_2.shape)
print(value_2.shape)
Out:
torch.Size([2])
torch.Size([2])
torch.Size([4])
我们可以推广这个过程来计算所有输入的剩余键和值元素,因为在后面计算未归一化的注意力权重时,我们将需要它们:
In:
keys = embedded_sentence @ W_query
values = embedded_sentence @ W_value
print(“keys.shape:”, keys.shape)
print(“values.shape:”, values.shape)
Out:
keys.shape: torch.Size([6, 2])
values.shape: torch.Size([6, 4])
现在我们已经有了所有必要的键和值,我们可以继续进行下一步,计算未归一化的注意力权重 ω(omega),如下图所示:
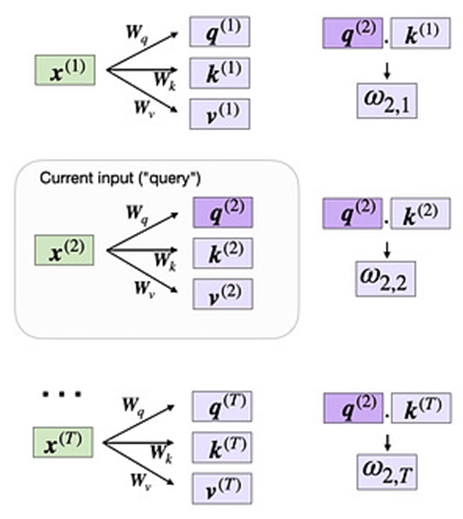
计算未归一化的注意力权重 ω(omega)
如上图所示,我们计算 ω_i,j 为查询和键序列之间的点积,即 ω_i,j = q(i) k(j)。
例如,我们可以计算查询和第5个输入元素(对应索引位置4)的未归一化注意力权重如下:
In:
omega_24 = query_2.dot(keys[4])
print(omega_24)
(请注意,ω是希腊字母“omega”的符号,因此上面的代码变量使用了相同的名称。)
Out:
tensor(1.2903)
由于我们将需要这些未归一化的注意力权重 ω 来计算后面的实际注意力权重,让我们计算所有输入令牌的 ω 值,如前面的图所示:
In:
omega_2 = query_2 @ keys.T
print(omega_2)
Out:
tensor([-0.6004, 3.4707, -1.5023, 0.4991, 1.2903, -1.3374])
计算注意力权重
自注意力中的后续步骤是将未归一化的注意力权重 ω 规范化,以获得规范化的注意力权重 α(alpha),通过应用 softmax 函数来实现。此外,1/√{d_k} 用于在通过 softmax 函数进行规范化之前对 ω 进行缩放,如下所示:
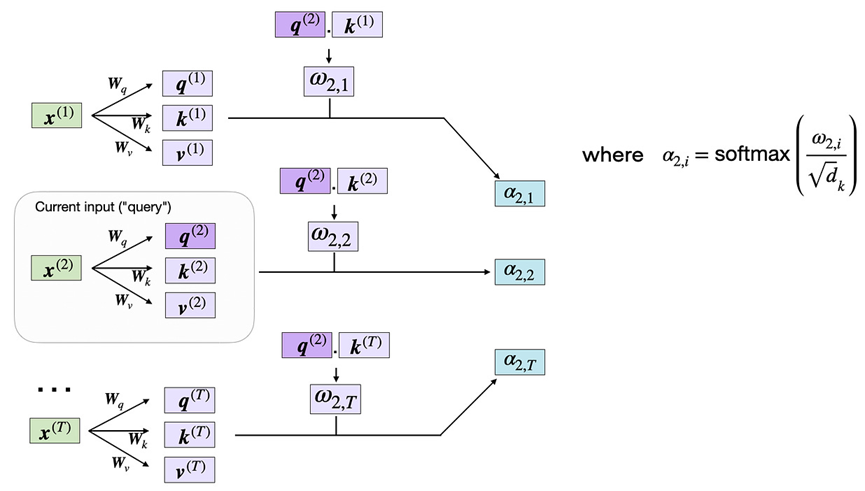
计算规范化的注意力权重 α
通过 d_k 缩放确保权重向量的欧几里得长度大致相同的量级。这有助于防止注意力权重变得太小或太大,这可能导致数值不稳定性或影响模型在训练过程中的收敛能力。
在代码中,我们可以实现注意力权重的计算如下:
In:
import torch.nn.functional as F
attention_weights_2 = F.softmax(omega_2 / d_v**0.5, dim=0)
print(attention_weights_2)
Out:
tensor([0.0386, 0.6870, 0.0204, 0.0840, 0.1470, 0.0229])
最后一步是计算上下文向量 z(2),它是我们原始查询输入 x(2) 的注意力加权版本,通过注意力权重包括所有其他输入元素作为其上下文:
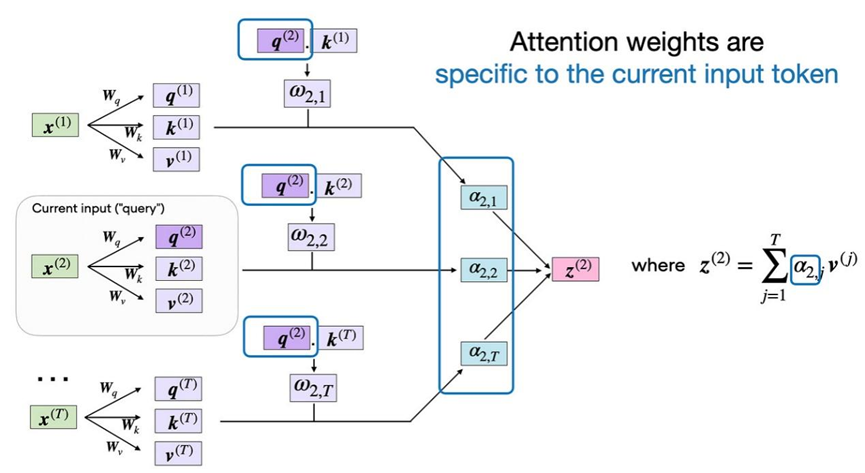
注意力权重是特定于某个输入元素的。在这里,我们选择了输入元素 x(2)
在代码中,这看起来如下:
In:
context_vector_2 = attention_weights_2 @ values
print(context_vector_2.shape)
print(context_vector_2)
Out:
torch.Size([4])
tensor([0.5313, 1.3607, 0.7891, 1.3110])
请注意,此输出向量的维度比原始输入向量(d = 3)更多,因为我们之前指定了 d_v > d;然而,嵌入大小选择 d_v 是任意的。
自注意力
现在,为了完成上述以前部分中自注意力机制的代码实现,我们可以在一个紧凑的 SelfAttention 类中总结前面的代码:
In:
import torch.nn as nn
class SelfAttention(nn.Module):
def __init__(self, d_in, d_out_kq, d_out_v):
super().__init__()
self.d_out_kq = d_out_kq
self.W_query = nn.Parameter(torch.rand(d_in, d_out_kq))
self.W_key = nn.Parameter(torch.rand(d_in, d_out_kq))
self.W_value = nn.Parameter(torch.rand(d_in, d_out_v))
def forward(self, x):
keys = x @ self.W_key
queries = x @ self.W_query
values = x @ self.W_value
attn_scores = queries @ keys.T # unnormalized attention weights
attn_weights = torch.softmax(
attn_scores / self.d_out_kq**0.5, dim=-1
)
context_vec = attn_weights @ values
return context_vec
根据 PyTorch 的约定,上面的 SelfAttention 类在 __init__ 方法中初始化自注意力参数,并通过 forward 方法计算所有输入的注意力权重和上下文向量。我们可以如下使用这个类:
In:
torch.manual_seed(123)
# reduce d_out_v from 4 to 1, because we have 4 heads
d_in, d_out_kq, d_out_v = 3, 2, 4
sa = SelfAttention(d_in, d_out_kq, d_out_v)
print(sa(embedded_sentence))
Out:
tensor([[-0.1564, 0.1028, -0.0763, -0.0764],
[ 0.5313, 1.3607, 0.7891, tensor([[-0.1564, 0.1028, -0.0763, -0.0764],
[ 0.5313, 1.3607, 0.7891, 1.3110],
[-0.3542, -0.1234, -0.2627, -0.3706],
[ 0.0071, 0.3345, 0.0969, 0.1998],
[ 0.1008, 0.4780, 0.2021, 0.3674],
[-0.5296, -0.2799, -0.4107, -0.6006]], grad_fn=<MmBackward0>)
如果你看第二行,你会发现它与前面部分的 context_vector_2 中的值完全相匹配:tensor([0.5313,
1.3607, 0.7891, 1.3110])。
多头注意力
在本文顶部的第一个图中(为方便起见下面再次显示),我们看到 Transformer使用了一个名为多头注意力的模块。
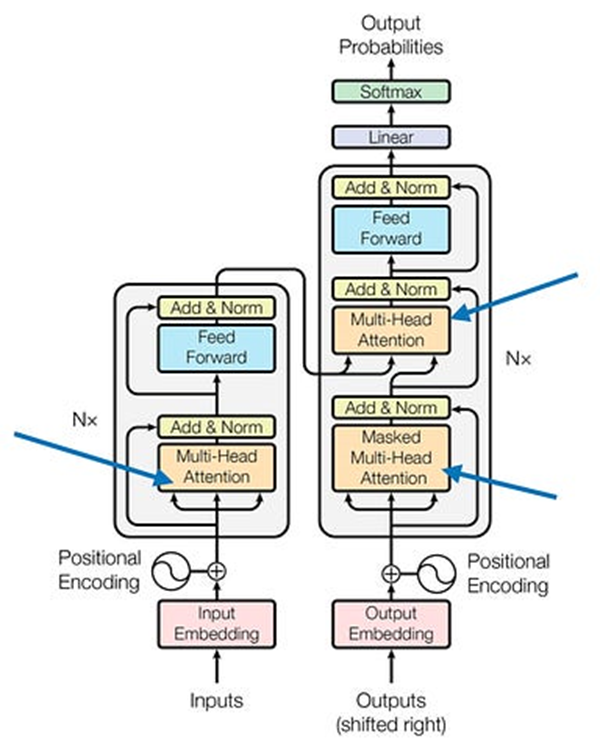
原始
Transformer架构中的多头注意力模块来自https://arxiv.org/abs/1706.03762
这个“多头”注意力模块与我们上面介绍的自注意力机制(缩放点积注意力)有何关系?
在缩放点积注意力中,输入序列使用表示查询、键和值的三个矩阵进行转换。在多头注意力的上下文中,这三个矩阵可以被视为一个单一的注意力头。下面的图总结了我们之前介绍和实现的这个单一注意力头:
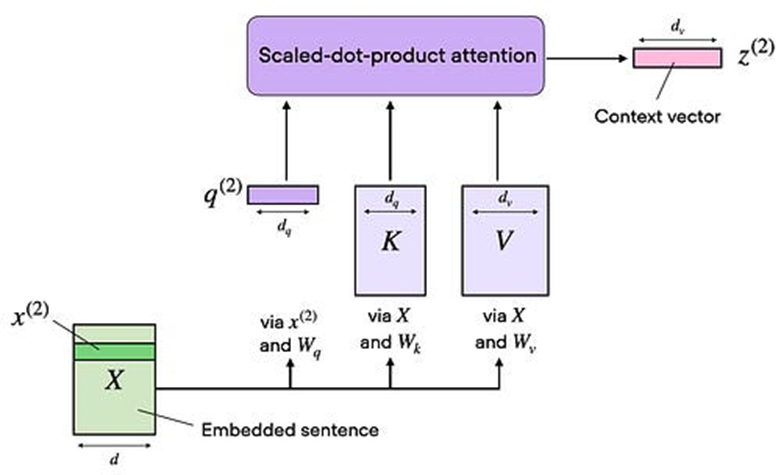
总结之前实现的自注意力机制
顾名思义,多头注意力涉及多个这样的头,每个头都包含查询、键和值矩阵。这个概念类似于在卷积神经网络中使用多个卷积核,产生具有多个输出通道的特征图。
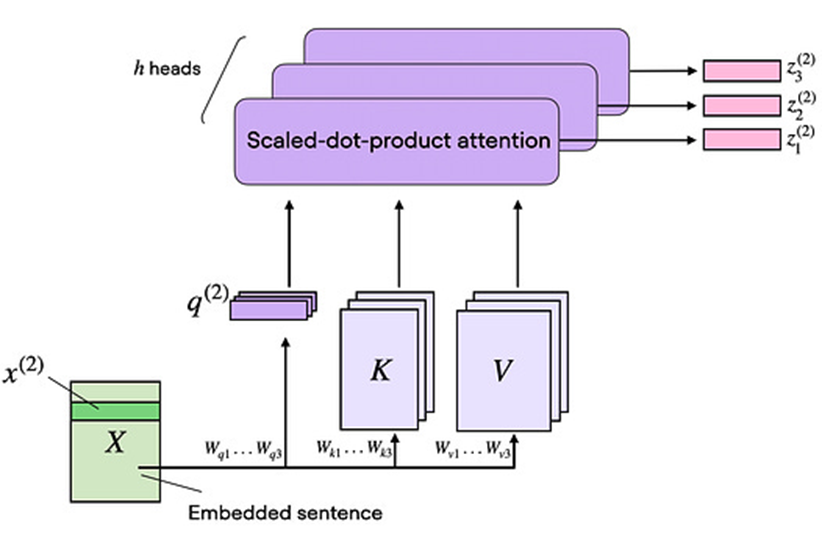
多头注意力:具有多个头的自注意力
为了在代码中说明这一点,我们可以为之前的 SelfAttention 类编写一个MultiHeadAttentionWrapper 类:
class MultiHeadAttentionWrapper(nn.Module):
def __init__(self, d_in, d_out_kq, d_out_v, num_heads):
super().__init__()
self.heads = nn.ModuleList(
[SelfAttention(d_in, d_out_kq, d_out_v)
for _ in range(num_heads)]
)
def forward(self, x):
return torch.cat([head(x) for head in self.heads], dim=-1)
d_* 参数与 SelfAttention 类中之前的相同——这里唯一的新输入参数是注意力头的数量:
-
d_in: Dimension of the input feature
vector. -
d_out_kq: Dimension for both query and
key outputs. -
d_out_v: Dimension for value outputs. -
num_heads: Number of attention heads.
我们使用这些输入参数 num_heads 次初始化 SelfAttention 类。我们使用 PyTorch 的 nn.ModuleList 来存储这些多个 SelfAttention 实例。
然后,前向传播涉及独立地将每个 SelfAttention 头(存储在 self.heads 中)应用于输入 x。然后,每个头的结果沿着最后一个维度(dim=-1)连接在一起。让我们在下面看一下!
首先,假设我们有一个单一的 Self-Attention 头,输出维度为 1,以保持简单用于说明的目的:
In:
torch.manual_seed(123)
d_in, d_out_kq, d_out_v = 3, 2, 1
sa = SelfAttention(d_in, d_out_kq, d_out_v)
print(sa(embedded_sentence))
Out:
tensor([[-0.0185],
[ 0.4003],
[-0.1103],
[ 0.0668],
[ 0.1180],
[-0.1827]], grad_fn=<MmBackward0>)
现在,让我们将这个扩展到 4 个注意力头:
In:
torch.manual_seed(123)
block_size = embedded_sentence.shape[1]
mha = MultiHeadAttentionWrapper(
d_in, d_out_kq, d_out_v, num_heads=4
)
context_vecs = mha(embedded_sentence)
print(context_vecs)
print(“context_vecs.shape:”, context_vecs.shape)
Out:
tensor([[-0.0185, 0.0170, 0.1999, -0.0860],
[ 0.4003, 1.7137, 1.3981, 1.0497],
[-0.1103, -0.1609, 0.0079, -0.2416],
[ 0.0668, 0.3534, 0.2322, 0.1008],
[ 0.1180, 0.6949, 0.3157, 0.2807],
[-0.1827, -0.2060, -0.2393, -0.3167]], grad_fn=<CatBackward0>)
context_vecs.shape: torch.Size([6, 4])
根据上面的输出,您可以看到先前创建的单一自注意力头现在表示上面输出张量中的第一列。
请注意,多头注意力的结果是一个 6×4 维度的张量:我们有 6 个输入令牌和 4 个自注意力头,其中每个自注意力头返回一个 1 维输出。在之前的自注意力部分中,我们也产生了一个 6×4 维度的张量。那是因为我们将输出维度设置为 4 而不是 1。实际上,如果我们可以在 SelfAttention 类本身中调整输出嵌入大小,为什么我们甚至需要多个注意力头呢?
单一自注意力头增加输出维度与使用多个注意力头之间的区别在于模型如何处理和学习数据。虽然这两种方法都增加了模型表示数据的能力,但它们在本质上以不同的方式做到这一点。
例如,多头注意力中的每个注意力头都有可能学习关注输入序列的不同部分,捕捉数据中的各种方面或关系。这种表示的多样性对于多头注意力的成功至关重要。
多头注意力还可能更有效,特别是在并行计算方面。
交叉注意力
在上面的代码演示中,我们设置了 d_q = d_k = 2 和 d_v = 4。换句话说,我们对查询和键序列使用相同的维度。虽然值矩阵 W_v 通常被选择为与查询和键矩阵相同的维度(例如在 PyTorch 的 MultiHeadAttention 类中),但我们可以为值的维度选择任意数量。
由于维度有时有点难以跟踪,让我们在下面的图中总结到目前为止我们所涵盖的一切,该图描绘了单个注意力头的各种张量大小。
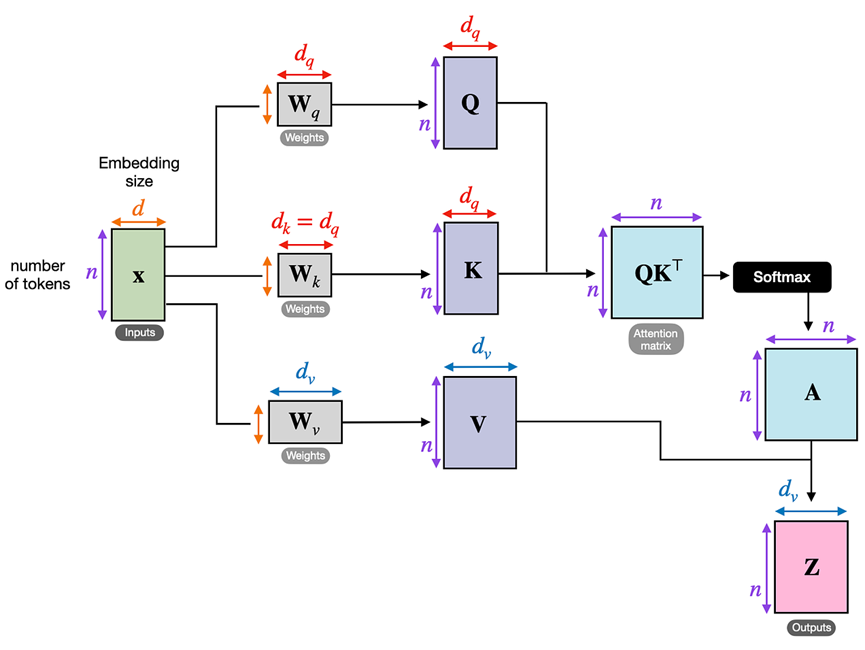
之前实现的自注意力机制的另一种视图,重点是矩阵的维度
现在,上面的插图对应于 Transformer中使用的自注意力机制。我们尚未讨论的这种注意力机制的一个特定变体是交叉注意力。
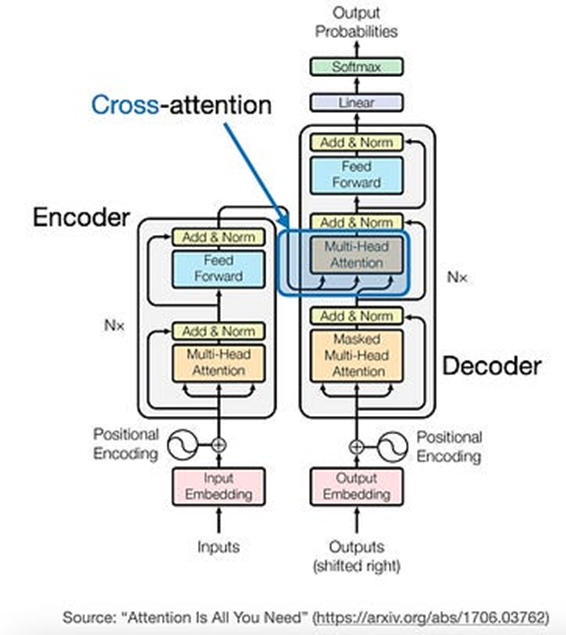
什么是交叉注意力,它与自注意力有何不同
在自注意力中,我们处理相同的输入序列。在交叉注意力中,我们混合或组合两个不同的输入序列。在上面的原始 Transformer架构中,这是左侧由编码器模块返回的序列和右侧由解码器部分处理的输入序列。
请注意,在交叉注意力中,两个输入序列 x_1 和 x_2 可以具有不同数量的元素。但是,它们的嵌入维度必须匹配。
下图说明了交叉注意力的概念。如果我们设置 x_1 = x_2,则等效于自注意力。
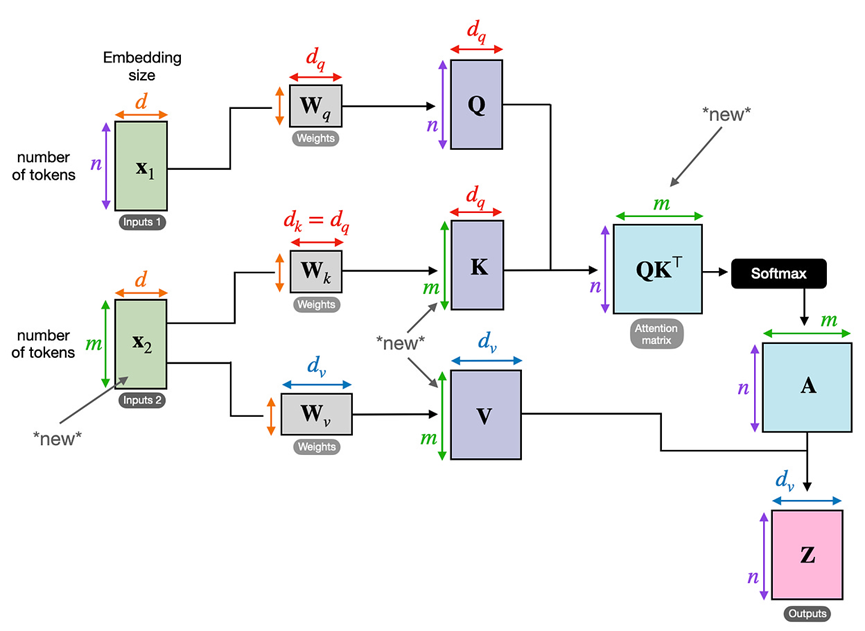
请注意,查询通常来自解码器,而键和值通常来自编码器
这在代码中如何工作?我们将采用并修改我们在“自注意力”部分中先前实现的SelfAttention类,只进行一些小的修改:
In:
class CrossAttention(nn.Module):
def __init__(self, d_in, d_out_kq, d_out_v):
super().__init__()
self.d_out_kq = d_out_kq
self.W_query = nn.Parameter(torch.rand(d_in, d_out_kq))
self.W_key = nn.Parameter(torch.rand(d_in, d_out_kq))
self.W_value = nn.Parameter(torch.rand(d_in, d_out_v))
def forward(self, x_1, x_2): # x_2 is new
queries_1 = x_1 @ self.W_query
keys_2 = x_2 @ self.W_key # new
values_2 = x_2 @ self.W_value # new
attn_scores = queries_1 @ keys_2.T # new
attn_weights = torch.softmax(attn_scores / self.d_out_kq**0.5, dim=-1)
context_vec = attn_weights @ values_2
return context_vec
CrossAttention类与先前的SelfAttention类之间的差异如下:
– forward方法接受两个不同的输入,x_1 和 x_2。查询来自 x_1,而键和值来自 x_2。这意味着注意力机制正在评估两个不同输入之间的交互。
– 注意力分数是通过取查询(来自 x_1)和键(来自 x_2)的点积来计算的。
– 与SelfAttention类似,每个上下文向量都是值的加权和。但是,在CrossAttention中,这些值来自第二个输入(x_2),权重基于 x_1 和 x_2 之间的交互。
让我们看看它的实际运行:
In:
torch.manual_seed(123)
d_in, d_out_kq, d_out_v = 3, 2, 4
crossattn = CrossAttention(d_in, d_out_kq, d_out_v)
first_input = embedded_sentence
second_input = torch.rand(8, d_in)
print(“First input shape:”, first_input.shape)
print(“Second input shape:”, second_input.shape)
In:
First input shape: torch.Size([6, 3])
Second input shape: torch.Size([8, 3])
请注意,计算交叉注意力时,第一个和第二个输入不必具有相同数量的标记(这里是行):
In:
context_vectors = crossattn(first_input, second_input)
print(context_vectors)
print(“Output shape:”, context_vectors.shape)
Out:
tensor([[0.4231, 0.8665, 0.6503, 1.0042],
[0.4874, 0.9718, 0.7359, 1.1353],
[0.4054, 0.8359, 0.6258, 0.9667],
[0.4357, 0.8886, 0.6678, 1.0311],
[0.4429, 0.9006, 0.6775, 1.0460],
[0.3860, 0.8021, 0.5985, 0.9250]], grad_fn=<MmBackward0>)
Output shape: torch.Size([6, 4])
我们在上面谈了很多关于语言 Transformers的内容。在原始的变换器架构中,当我们从一个输入句子到语言翻译的输出句子时,交叉注意力是有用的。输入句子代表一个输入序列,翻译代表第二个输入序列(两个句子的单词数量可以不同)。
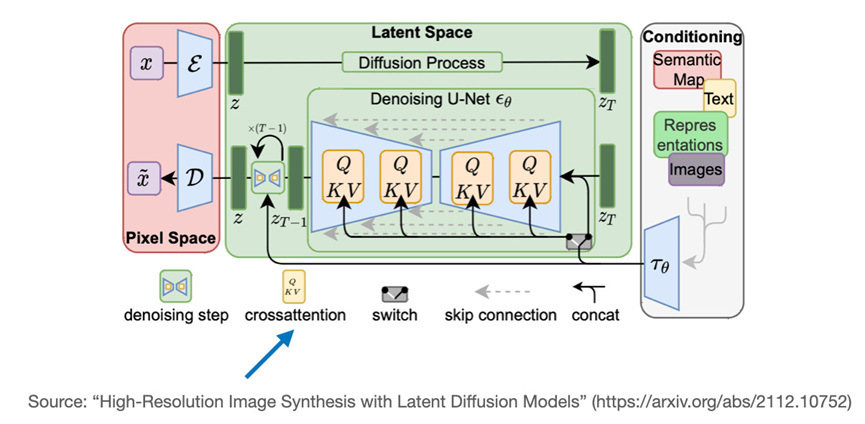
另一个使用交叉注意力的流行模型是稳定扩散。稳定扩散在U-Net模型中的生成图像与用于条件处理的文本提示之间使用交叉注意力,正如《使用潜在扩散模型进行高分辨率图像合成》中所述——这是描述稳定扩散模型的原始论文,后来由Stability AI采用以实现流行的稳定扩散模型。
因果自注意力
在这一节中,我们将先前讨论的自注意力机制调整为因果自注意力机制,专门用于生成文本的类GPT(解码器风格)LLMs。这种因果自注意力机制通常也被称为“掩码自注意力”。在原始的 Transformer架构中,它对应于“掩码多头注意力”模块——为简单起见,本节我们将只看一个注意力头,但相同的概念可以推广到多个头。
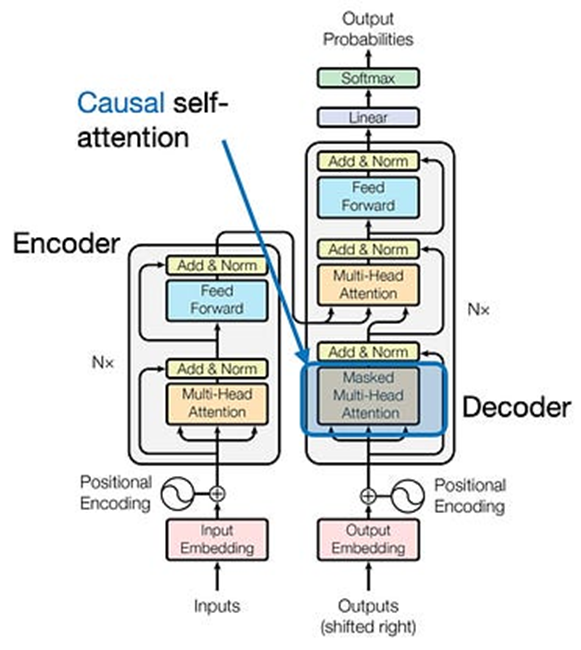
原始
Transformer架构中的因果自注意模块(通过“Attention Is All You
Need”,https://arxiv.org/abs/1706.03762)
因果自注意力确保序列中某个位置的输出仅基于先前位置的已知输出,而不是未来位置。简而言之,它确保每个下一个单词的预测仅取决于前面的单词。为了在类似GPT的LLMs中实现这一点,对于每个处理的令牌,我们会掩盖掉输入文本中当前令牌后面的未来令牌。
在下面的图中,演示了在输入中隐藏未来令牌的因果掩码对注意权重的应用。
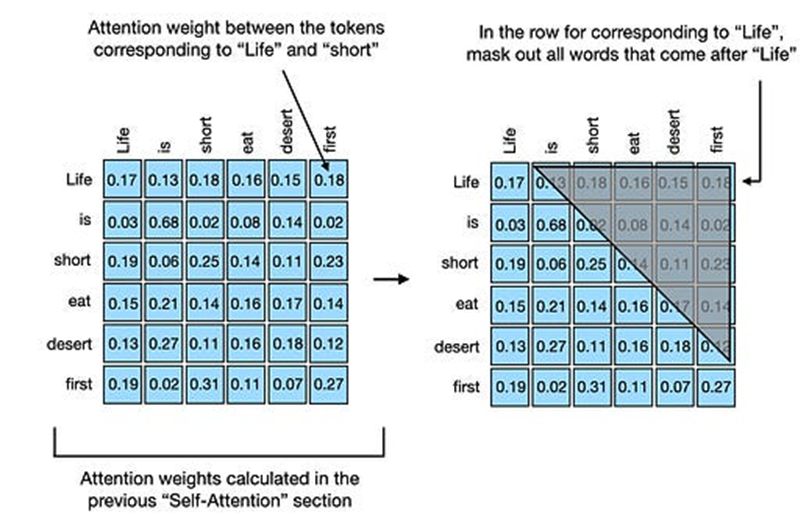
为了说明和实现因果自注意,让我们使用前面部分的未加权注意分数和注意权重。首先,我们快速回顾一下前面自我注意部分中的注意分数的计算:
In:
torch.manual_seed(123)
d_in, d_out_kq, d_out_v = 3, 2, 4
W_query = nn.Parameter(torch.rand(d_in, d_out_kq))
W_key = nn.Parameter(torch.rand(d_in, d_out_kq))
W_value = nn.Parameter(torch.rand(d_in, d_out_v))
x = embedded_sentence
keys = x @ W_key
queries = x @ W_query
values = x @ W_value
# attn_scores are the “omegas”,
# the unnormalized attention weights
attn_scores = queries @ keys.T
print(attn_scores)
print(attn_scores.shape)
Out:
tensor([[ 0.0613, -0.3491, 0.1443, -0.0437, -0.1303, 0.1076],
[-0.6004, 3.4707, -1.5023, 0.4991, 1.2903, -1.3374],
[ 0.2432, -1.3934, 0.5869, -0.1851, -0.5191, 0.4730],
[-0.0794, 0.4487, -0.1807, 0.0518, 0.1677, -0.1197],
[-0.1510, 0.8626, -0.3597, 0.1112, 0.3216, -0.2787],
[ 0.4344, -2.5037, 1.0740, -0.3509, -0.9315, 0.9265]],
grad_fn=<MmBackward0>)
torch.Size([6, 6])
与之前的自我注意部分一样,上面的输出是一个包含6个输入令牌的这些成对未标准化注意权重(也称为注意分数)的6×6张量。
之前,我们通过softmax函数计算了经缩放的点积注意力,如下所示:
In:
attn_weights = torch.softmax(attn_scores / d_out_kq**0.5, dim=1)
print(attn_weights)
Out:
tensor([[0.1772, 0.1326, 0.1879, 0.1645, 0.1547, 0.1831],
[0.0386, 0.6870, 0.0204, 0.0840, 0.1470, 0.0229],
[0.1965, 0.0618, 0.2506, 0.1452, 0.1146, 0.2312],
[0.1505, 0.2187, 0.1401, 0.1651, 0.1793, 0.1463],
[0.1347, 0.2758, 0.1162, 0.1621, 0.1881, 0.1231],
[0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],
grad_fn=<SoftmaxBackward0>)
上述的6×6输出表示注意权重,我们在之前的自我注意部分中也进行了计算。
现在,在类似GPT的LLMs中,我们训练模型以一次从左到右读取并生成一个标记(或单词)。如果我们有一个训练文本样本,比如”Life is short eat desert first”,我们有以下的设置,其中右箭头右侧的单词的上下文向量只应包含它本身和前面的单词:
– “Life”
→ “is”
– “Life
is” → “short”
– “Life is
short” → “eat”
– “Life is
short eat” → “desert”
– “Life is
short eat desert” → “first”
实现上述设置的最简单方法是通过在对角线之上的注意权重矩阵上应用掩码来屏蔽所有未来标记,如下图所示。这样,创建上下文向量时将不包括“未来”单词,这些向量是通过对输入进行加权和求和创建的。
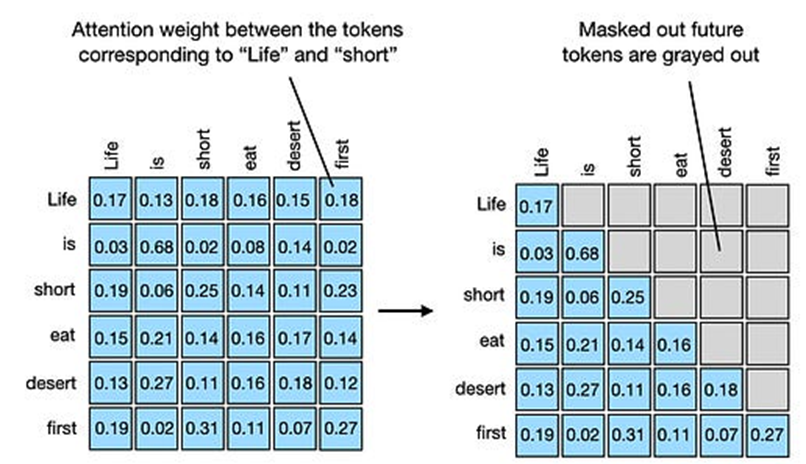
[图:应用掩码以隐藏未来令牌的注意权重矩阵]
使用此掩码将注意权重置零以清除对角线以上的所有注意权重:
In:
block_size = attn_scores.shape[0]
mask_simple = torch.tril(torch.ones(block_size, block_size))
print(mask_simple)
Out:
tensor([[1., 0., 0., 0., 0., 0.],
[1., 1., 0., 0., 0., 0.],
[1., 1., 1., 0., 0., 0.],
[1., 1., 1., 1., 0., 0.],
[1., 1., 1., 1., 1., 0.],
[1., 1., 1., 1., 1., 1.]])
接下来,我们将注意力权重与此掩码相乘,将对角线以上的所有注意力权重都置零:
In:
masked_simple = attn_weights*mask_simple
print(masked_simple)
Out:
tensor([[0.1772, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0386, 0.6870, 0.0000, 0.0000, 0.0000, 0.0000],
[0.1965, 0.0618, 0.2506, 0.0000, 0.0000, 0.0000],
[0.1505, 0.2187, 0.1401, 0.1651, 0.0000, 0.0000],
[0.1347, 0.2758, 0.1162, 0.1621, 0.1881, 0.0000],
[0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],
grad_fn=<MulBackward0>)
尽管上述方法是屏蔽未来单词的一种方式,但请注意每行中的注意权重不再总和为1。为了缓解这一点,我们可以规范化行,使它们再次总和为1,这是注意权重的标准约定:
In:
row_sums = masked_simple.sum(dim=1, keepdim=True)
masked_simple_norm = masked_simple / row_sums
print(masked_simple_norm)
Out:
输出如下:
tensor([[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0532, 0.9468, 0.0000, 0.0000, 0.0000, 0.0000],
[0.3862, 0.1214, 0.4924, 0.0000, 0.0000, 0.0000],
[0.2232, 0.3242, 0.2078, 0.2449, 0.0000, 0.0000],
[0.1536, 0.3145, 0.1325, 0.1849, 0.2145, 0.0000],
[0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],
grad_fn=<DivBackward0>)
正如我们所看到的,每行中的注意权重现在总和为1。
在神经网络中规范化注意权重,例如在 Transformer模型中,比未规范化的权重具有两个主要优势。首先,总和为1的规范化注意权重类似于概率分布。这使得更容易通过比例来解释模型对输入各部分的关注。其次,通过将注意权重限制为总和为1,这种规范化有助于控制权重和梯度的尺度,从而改善训练动力学。
更高效的掩码无需重新规范化
在我们上面编写的因果自注意过程中,我们首先计算注意分数,然后计算注意权重,屏蔽对角线以上的注意权重,最后重新规范化注意权重。这在下图中进行了总结:

先前实施的因果自注意过程
或者,有一种更有效的方法可以实现相同的结果。在这种方法中,我们取注意分数,并在输入softmax函数计算注意权重之前,用负无穷替换对角线上方的值。这在下图中进行了总结:

替代性、更有效的实施因果自注意的方法
我们可以使用以下PyTorch代码编写此过程,首先对对角线以上的注意力得分进行掩码:
In:
mask = torch.triu(torch.ones(block_size, block_size))
masked = attn_scores.masked_fill(mask.bool(), -torch.inf)
print(masked)
上面的代码首先创建一个掩码,对角线以下为0,对角线以上为1。这里,`torch.triu`(保留上三角)保留矩阵的主对角线及其以上的元素,将其以下的元素置零,从而保留上三角部分。相反,`torch.tril`(保留下三角)保留主对角线及其以下的元素。
`masked_fill`方法然后使用正掩码值(1)替换正值以上对角线的所有元素为`-torch.inf`,结果如下所示:
Out:
tensor([[ 0.0613, -inf, -inf, -inf, -inf, -inf],
[-0.6004, 3.4707, -inf, -inf, -inf, -inf],
[ 0.2432, -1.3934, 0.5869, -inf, -inf, -inf],
[-0.0794, 0.4487, -0.1807, 0.0518, -inf, -inf],
[-0.1510, 0.8626, -0.3597, 0.1112, 0.3216, -inf],
[ 0.4344, -2.5037, 1.0740, -0.3509, -0.9315, 0.9265]],
grad_fn=<MaskedFillBackward0>)
然后,我们只需像往常一样应用softmax函数,即可获得归一化和带掩码的注意权重:
In:
attn_weights = torch.softmax(masked / d_out_kq**0.5, dim=1)
print(attn_weights)
Out:
tensor([[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0532, 0.9468, 0.0000, 0.0000, 0.0000, 0.0000],
[0.3862, 0.1214, 0.4924, 0.0000, 0.0000, 0.0000],
[0.2232, 0.3242, 0.2078, 0.2449, 0.0000, 0.0000],
[0.1536, 0.3145, 0.1325, 0.1849, 0.2145, 0.0000],
[0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],
grad_fn=<SoftmaxBackward0>)
为什么这样做会奏效呢?在上一步中应用的softmax函数将输入值转换为概率分布。当输入中存在`-inf`时,softmax有效地将其视为零概率。这是因为e^(-inf)趋近于0,因此这些位置对输出概率不起作用。
结论
在本文中,我们通过逐步的编码方法探讨了自注意机制的内部工作原理。在此基础上,我们进一步研究了多头注意力,这是大型语言变换器的基本组成部分。
我们还编写了交叉注意力的代码,这是自注意的一种变体,当应用于两个不同的序列之间时特别有效。最后,我们编写了因果自注意的代码,这是解码器式LLM(如GPT和Llama)中生成连贯和上下文适当序列的重要概念。
通过从头开始编写这些复杂的机制,您希望能够更好地理解变换器和LLM中使用的自注意机制的内部工作原理。
(请注意,本文中提供的代码仅供说明目的。如果您计划为培训LLM实施自注意,我建议考虑像Flash Attention这样的优化实现,它可以减少内存占用和计算负担。)

想要了解更多,欢迎入群交流!
权益福利:
1、AI 行业、生态和政策等前沿资讯解析;
2、最新 AI 技术包括大模型的技术前沿、工程实践和应用落地交流(社群邀请人数已达上限,可先加小编微信:15937102830)

关于MoPaaS魔泊云
源于硅谷、扎根中国,上海殷泊信息科技有限公司 (MoPaaS) 是中国领先的人工智能(AI)平台和服务提供商,为用户的数字转型、智能升级和融合创新直接赋能。针对中国AI应用和工程市场的需求,基于自主的智能云平台专利技术,MoPaaS 在业界率先推出新一代开放的AI平台为加速客户AI技术创新和应用落地提供高效的算力优化和规模化AI模型开发、部署和运维 (ModelOps) 能力和服务;特别是针对企业应用场景,提供包括大模型迁移适配、提示工程以及部署推理的端到端 LLMOps方案。MoPaaS AI平台已经服务在工业制造、能源交通、互联网、医疗卫生、金融技术、教学科研、政府等行业超过300家国内外满意的客户的AI技术研发、人才培养和应用落地工程需求。MoPaaS致力打造全方位开放的AI技术和应用生态。MoPaaS 被Forrester评为中国企业级云平台市场的卓越表现者 (Strong Performer)。

END
▼ 往期精选 ▼



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


