雨水 | 量子错误缓解初探

在量子信息传输以及量子比特门作用过程中，都会存在有噪声的干扰。错误缓解方法可以一定程度上减少这些噪声对测量值的影响。

我们用  表示理想量子门，相应的量子信道表示为相应的信道表示为   。这里的量子信道是一个从矩阵到矩阵的映射，如对于密度矩阵  ，  。带有噪声的量子门对应的量子信道可以写为  ，其中  是噪声信道。为简单起见，我们假设门误差是马尔可夫的，也就是说，不同门的噪声信道  是独立的。

对于一个输入状态  ，理想输出状态  可以写为[1] 

而我们在实际中获得的含有噪声输出状态  则为 

这里  是量子门的数量。

当噪声低于一定阈值时，我们可以利用量子纠错（QEC）来将含噪声的态恢复成理想状态。然而，由于实现该方案需要制备大量纠缠的量子比特，对于近期含有噪声的中等规模的量子设备（NISQ）来说，QEC 可能还并不实用。

尽管在 NISQ 设备上采用 QEC 方法将含噪声态恢复成理想状态还很困难，研究者们发展出了量子错误缓解（QEM）的方法作为一种替代方案。这一类方案的目标并不是恢复输出态，而是采用一些对测量结果后处理手段，恢复可观测量的统计平均值。QEM 由于不像 QEC 那样需要大量的辅助比特，实行起来对设备的要求更低，但由于 QEM 往往会有更大的统计方差，相比 QEC 需要测量的重复次数也要更多。

具体来说，假设我们在输出状态上测量一个可观测量  ，QEM 方法旨在通过对一组含噪声量子线路的测量结果进行经典后处理来恢复：

这里的  表示求迹。

具体而言，有哪些错误缓解的方法呢？外推法在不同的物理错误率下运行相同的量子线路，从而通过不同错误率对应的测量结果外推得到无错误情况下的观测结果（如图1，利用错误率为  时的可观测量  的平均值  以及错误率为  时的可观测量  的平均值  外推得到无噪声时的可观测量  的平均值  ）。除此之外也有最小二乘拟合法[2]，随机错误缓解[3]，基于机器学习错误缓解[4]，量子子空间展开等方法[5]。

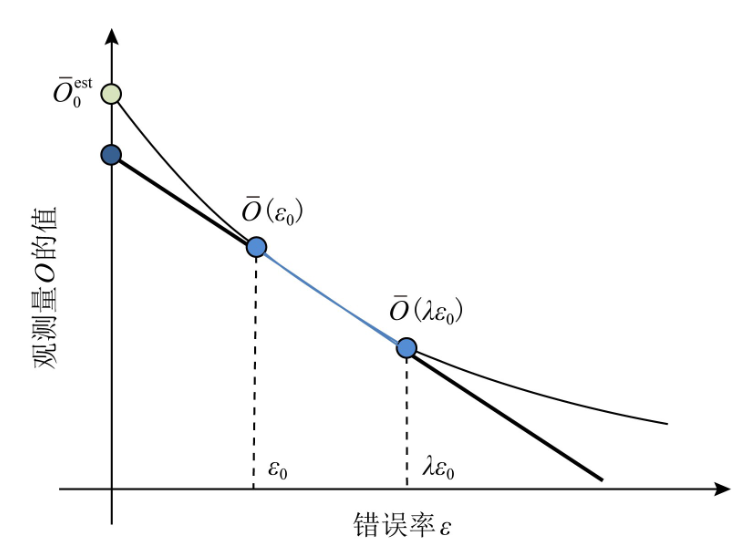
图1 外推法图示[6]

目前，量子错误缓解仍然存在有巨大的发展潜力，对在 NISQ 设备中实现量子计算有重要的价值，是一种可靠的降噪手段。如何利用量子错误缓解技术，提高各个量子算法的实现精度值得科学界的进一步探索研究。

参考文献

[1] Yukun Z., Xiao Y., Quantum Error Mitigation: A Review, Journal of Computer Research and Development, 58(9), 059 (2021).

[2] Otten M., Gray S.K. , Recovering noise-free quantum observables, Physical Review A, 99(1): 012338 (2019).

[3] Jinzhao S., Xiao Y., Tsunoda T., et al., Mitigating realistic noise in practical noisy intermediate-scale quantum devices, Physical Review Applied, 15(3) : 034026 (2021).

[4] Piotr C., Andrew A., Patrick J. C., et al., Error mitigation with Clifford quantum-circuit data, Quantum 5, 592 (2021).

[5] McClean J. R., Kimchi-Schwartz M. E., Carter J., et al., Hybrid quantum-classical hierarchy for mitigation of decoherence and determination of excited states, Physical Review A, 95(4): 042308 (2017).

[6] McArdle S. ,Endo S., Aspuru-Guzik A., et al. , Quantum computational chemistry, Reviews of Modern Physics, 92(1): 015003 (2020).

文 | 陆洋宇

图 | 朱成轩

—   版权声明  —

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。