新年随笔：从《你一生的故事》到控制论

625次阅读

新年随笔：从《你一生的故事》到控制论

导语

控制论是最早起源于上世纪维纳时代的一门古老学问，作为一套数学框架却持续启发后来的理论技术创新，包括强化学习的创新源头即来源于控制论。本文是集智俱乐部资深粉丝、曾创立国内最大跨学科社区的JK在新年期间撰写的随笔，从科幻电影《降临》开始，展现了控制论这门学问中的一小片花瓣——最优控制原理的美妙之处，邀请感兴趣的朋友们一起学习控制论，领略复杂系统控制之美。
集智学园联合中科院数学与系统科学研究院多位控制科学与工程领域专家共同开设《控制科学前沿理论与方法》系列课程，为面向控制专业领域学生以及跨领域的学习者做深度科普，帮助学习控制论的核心思想、框架与方法。此系列课程共计10节，从2024年4月2日起，每周二晚19:00-21:00线上上课。欢迎感兴趣的朋友报名参与！
研究领域：控制论，最优控制理论，神经微分方程，最小作用量原理，哈密顿力学
新年随笔：从《你一生的故事》到控制论 JK | 作者

从《降临》到“分析力学”

在科幻电影《降临》的原版小说《你一生的故事》中曾有这样的一个场景：一艘外星飞船莫名地降临到了地球。科学家们开始尝试与外星人接触，他们特别详细地向外星人表达了牛顿力学和微积分原理。然而，外星人却是一头雾水，完全不能理解。后来，科学家们换了一个思路，开始给外星人讲解最小作用量原理、拉格朗日力学，这才取得了重大的进展与突破，与外星人建立了沟通和联系。原来，这群外星人的思维方式与我们地球人完全不一样，他们的思考是建立在“目的论”的基础之上的，而这一点与18世纪的物理学家们发明的最小作用量原理有异曲同工的意思。

新年随笔：从《你一生的故事》到控制论

你把一个小球抛向天空，它划过一条优美的抛物线落了下去。这一切都可以完美地用牛顿运动定律进行解释。你分析每一时刻小球的受力状态，得到小球加速度的表达式，然后再运用微积分，积分得到小球在每一时刻的速度和位置，这就是牛顿力学的解题原理。

但拉格朗日力学则完全不是如此，它采用了一种“万物有灵”的观点来解释同样的小球运动现象。你别误会，我这里说的万物有灵，并不是它们真的有灵魂，而是说这个小球之所以沿着一条优美的抛物线运动是有它自己的“目的”的，这一目的就是所谓的“作用量”，它可以定义为每一时刻小球的动能减去势能沿着小球运动轨迹的积分。这样，小球之所以这样运动而不是那样运动，究其本质就在于它在优化它自己的作用量。于是，物理学们只需要求解一个泛函的极值问题就可以求解出小球真实的轨迹，这一计算结果与牛顿力学的方法一模一样。

新年随笔：从《你一生的故事》到控制论

其实，这个最小作用量原理，即用一种“万物有灵”的“目的论”思想来解释自然现象的疯狂做法可以追溯到著名的专业律师，业余数学家费马。他早在1662年就提出了著名的光行最速原理，即认为光之所以会走我们看到的这种路径，那是因为光在试图最小化从出发点到目标点的时间。因此，最小作用量原理可谓是由来已久了。

新年随笔：从《你一生的故事》到控制论
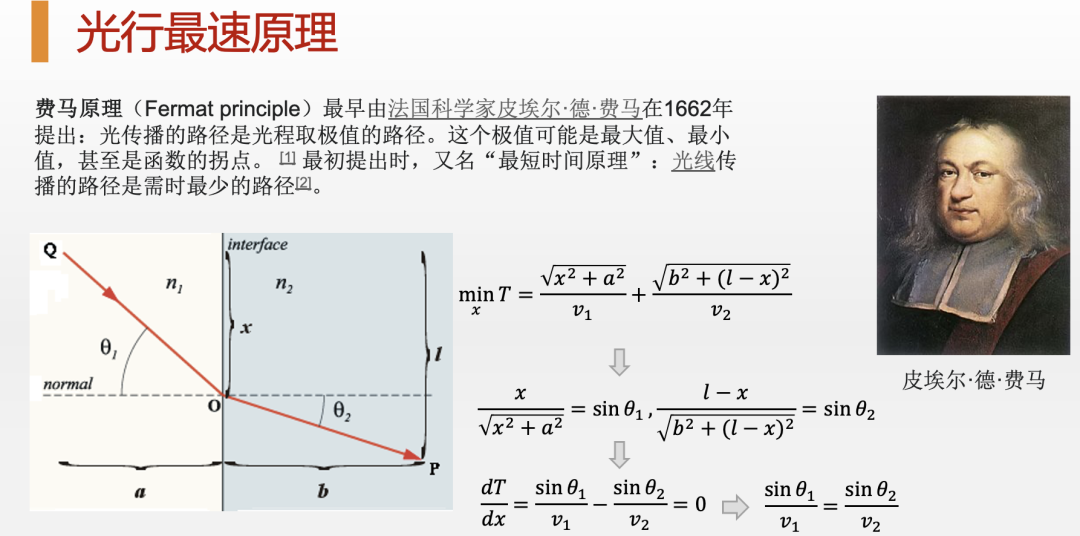
更有意思的是，当我们使用一种叫做“拉格朗日乘子法”的技巧来求解最小作用量的时候，则可以直接引出来物理学中的另外一个重要的物理量，这就是哈密顿量（Hamiltonian），也就是物理系统的总能量。如果你了解怎么用基本的微积分原理求解最优化问题，你就会知道，当我们考虑一个带约束的优化问题的时候，我们通常会把约束条件乘上一个拉格朗日因子（Lagrangian factor）放到目标函数中同原来的优化函数一起求解。还用刚刚那个被我们抛掷到空中的小球来说，它在运动的过程中除了试图最小化它的作用量之外，还要受到一系列的约束。比如，小球的运动轨迹不能太过任意，而必须遵循一条连续的，可以由微分方程描述的轨迹，那么我们就可以把这一条约束通过拉格朗日乘子法放到我们的优化目标之中。当然，在这个情形下，因为小球每时刻都要受到连续性约束，所以拉格朗日乘子就变成了一个连续的函数。

新年随笔：从《你一生的故事》到控制论
于是，这个新的，包括了拉格朗日乘子的优化函数就称为哈密顿量（Hamiltonian），也就是物理系统中的能量。对这个新优化问题的求解，我们就能得到一组新的方程，这就是物理中著名的哈密顿方程，而通过求解这些哈密顿方程，也能够同样得到和牛顿力学以及拉格朗日力学一模一样的运动轨迹。

新年随笔：从《你一生的故事》到控制论

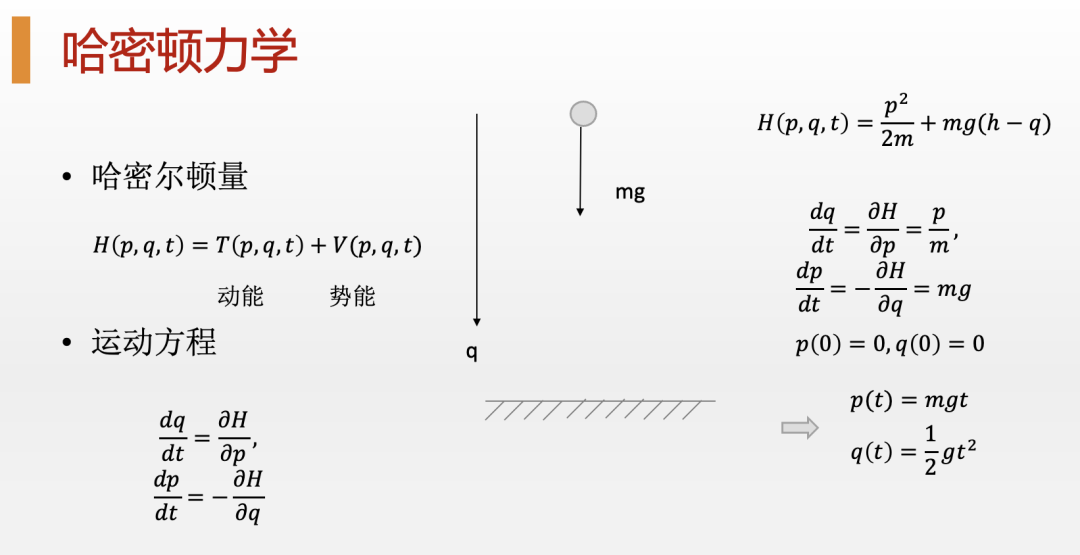
然而，这一套使用哈密顿量进行求解的物理学就被人们称为“哈密顿力学”。尽管这套力学其实与牛顿力学、拉格朗日力学等价，但在实际应用中哈密顿力学则要方便得多，因为我们通常很容易就能写出一个物理系统的能量函数，也就是哈密顿量，而进行受力分析则既过于复杂，又容易出错。更重要的是，无论是“最小作用量原理”还是“哈密顿力学”，它们都提供了一整套全新的思考方法，这种方法大大拓展了经典力学的应用领域，同时也更具有普遍性，甚至可以很方便地把这套方法扩展到量子力学等领域。这门学问就是现代大学理论物理专业必修的四大力学之首：“分析力学”。

从“最优控制理论”到“神经微分方程”

现在大家都在说“跨学科”研究，然而，什么是好的跨学科研究呢？显然，并不是你简单地把两门学科的概念、知识简单地拼凑在一起就算跨学科研究了。理想情况下，我们应当对不同学科的知识进行深层次的整合。而要想达到这个目的，第一步就是要找到不同学科在深层次上的联系。数学作为一切学科的通用语言，显然非常适合去干这件事儿。一旦我们用数学把一个物理问题抽象为一个符号和运算的框架，那么这个物理问题就可以被迁移到其它学科中去了。接下来，我将给你展示，如何把“最小作用量原理”，以及“拉格朗日乘子法”这套数学框架扩展到最优控制理论，甚至被誉为“无穷深度”的神经网络——神经微分方程（Neural Ordinary Differential Equation，简称Neural ODE）之上。

让我们回到最小作用量原理和拉格朗日乘子法，你会发现，这其实就是一个普通的带约束的最优化问题。但与我们通常求解的最优化略有不同的地方在于，待优化的不是一个或多个具体的变量，而是无穷多个变量，即一个或多个函数。而优化问题的求解方法，也是我们再熟悉不过的拉格朗日乘子法，但是由于约束条件也有无穷多个，于是拉格朗日乘子也被扩展到了无穷个，从而构成了函数。

其实，如果我们把具有物理含义的作用量以及相伴的拉格朗日量替换成更为普遍的函数，把约束条件换为更一般的微分方程，那么，整个这套数学框架和求解方法就可以被扩展到一般问题中去了。这于是就诞生了“最优控制理论”的理论框架。

比如，让我们考虑一个导弹的最优控制问题：你无非就是要求解一条导弹在三维空间中的飞行轨迹，使得导弹最终能够击中敌人的目标。你只需要把导弹对应为小球，把飞行轨迹对应为小球的轨迹，把最终落点与目标点的距离最小对应为最小化作用量，那么你就会发现，导弹的最优控制问题其实就是在最小作用量原理下的拉格朗日力学问题。

你不妨采用同样的方式，把导弹的飞行动力学作为约束条件加入这个优化问题中，你于是就得到了一个新的优化目标函数，这在数学上被称为对偶函数，在物理上称为哈密顿量，在最优控制理论中称为“广义的哈密顿量”。

新年随笔：从《你一生的故事》到控制论
有趣的是，当你求解这个新的泛函优化问题，你会得到两组微分方程，一个是我们熟悉的动力学方程，而另一个则被称为伴随方程。那个被我们引入的拉格朗日算子就成为了伴随方程的未知函数。

有意思的是，这个伴随方程的初始时间是整个轨迹的结束，因此，要想求解这个伴随方程，就必须沿着时间的反方向进行积分求解。也就是说，如果我们用数值迭代的方法（欧拉方法或Runge Kutta算法）求解这个伴随方程的时候，这个未知的伴随函数，也就是我们的拉格朗日乘子就会沿着时间反向一步步地迭代，这就仿佛有一个信号是反向传播的。如果我们再将这个伴随方程结合动力学方程一起来看，就会发现一个是前向传播，一个是反向传播，两者交互作用就可以得到最终方程组的解。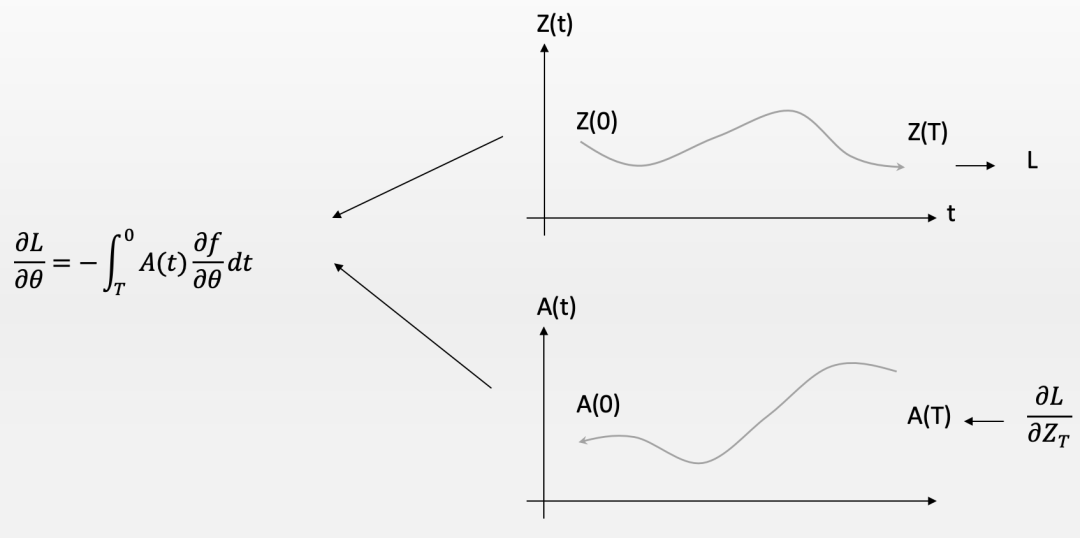
新年随笔：从《你一生的故事》到控制论
这让你想到了什么？是不是想到了训练神经网络的算法？一个神经网络都会分为运行阶段，这是信号的前向传播，另一个则是误差的反向传播，两者不停地迭代就构成了训练神经网络的著名的梯度下降算法。也就是说，训练神经网络的过程可以看作是一个最优控制过程的结果。
这一结论听起来非常玄幻，这是真的吗？事实上，在2018年发表的一篇论文就将训练神经网络的训练变成了一个最终求解动力学方程和伴随方程的过程。这就是著名的 Neural ODE（神经微分方程）的提出。
我们知道，随着AI技术的发展，人们逐渐意识到，随着网络层次的加深，神经网络的表现就会越来越好。那么，我们能不能把一个神经网络的深度加深到无限呢？答案是肯定的，这就是Neural ODE的神奇之处。它是怎么做到的呢？
新年随笔：从《你一生的故事》到控制论 Chen, Ricky TQ, et al. Neural ordinary differential equations. Advances in neural information processing systems 31 (2018).

原来，早在18年以前，人们就发明了一种高效的非常深度的神经网络。其中的关键就是在每一层有一个跳跃的链接，它可以直接连到这一层的输出上，并且它们的信号也是简单的加到了一起。这样的神经网络称为残差网络，它可以在图像识别等任务上达到非常好的结果。

这个时候，如果你做一个假设，即所有残差模块的参数是相同的，你就会发现残差网络的迭代运算过程像极了求解微分方程的数值算法：欧拉法。

新年随笔：从《你一生的故事》到控制论
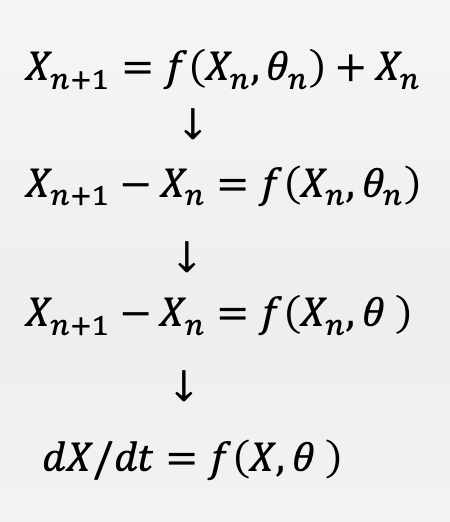
进一步，假如层数有很多，这些残差方程合在一起就构成了一个微分方程。于是，这就构成了Neural ODE的最基本思想。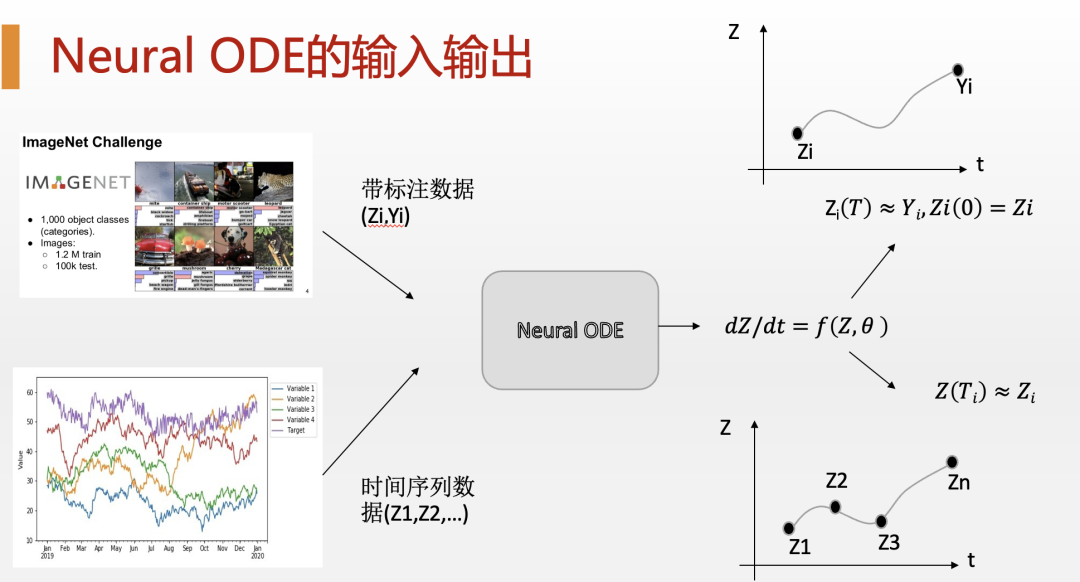

具体来讲，Neural ODE把神经网络训练的问题看成了一个最优控制问题。其中，目标函数就是依赖整个Neural ODE求解轨迹的函数，例如最小化神经网络输出与目标之间的误差，就非常像前面提到的导弹发射问题。而我们能够调整的就是神经网络各个层的参数，它能够最终影响最优的轨迹。那么，怎么找到这个最优的轨迹呢？这就要用到我们前面提到的前向微分方程和伴随微分方程了。而一旦你把这个伴随方程离散化，你就会发现，它其实就是神经网络的梯度迭代算法，而那个伴随函数，也就是我们的拉格朗日乘子就是在训练神经网络中反传的误差。

新年随笔：从《你一生的故事》到控制论

从梯度下降到强化学习

看来，无论是经典物理还是机器学习，我们都把它们统一为最优控制问题：为了明天的目标而规划今天的步骤，最终得到一条最优的行动路径。那么，如何找到这条最优路径呢？梯度下降是一种可能的方法，但它并不是人们常用的最好方法。
人们常用的解决最优控制的数值方法当属动态规划方法。动态规划的主要思想是将一个复杂问题分解为更简单的简单问题，从而进行迭代求解的一种方法，它是一种有效地求解离散最优控制问题的方法，被称为最优控制理论的三大基石之一。
在动态规划的求解过程中，会涉及到一个所谓的价值函数（Value function）的迭代求值。动态规划的过程就是一方面正确地为每个状态进行价值评估（即给价值函数赋值），另一方面就是根据这个价值评估选择最优的行动，从而形成最终的决策路径。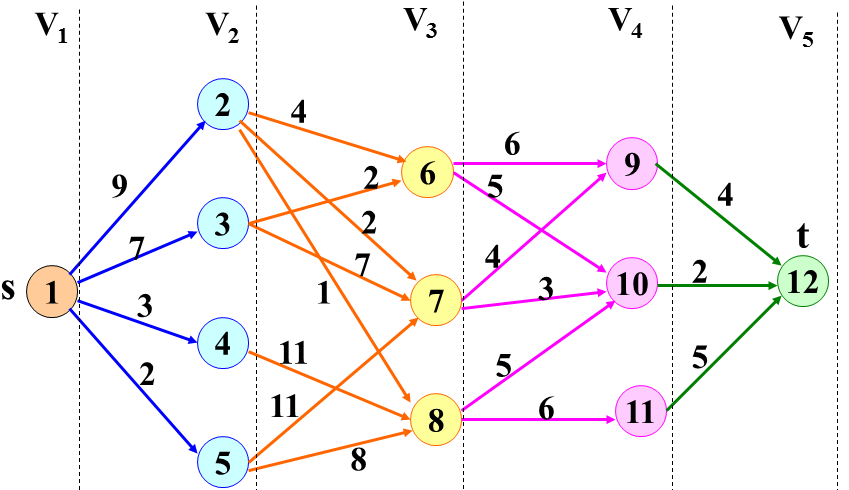
新年随笔：从《你一生的故事》到控制论动态规划与价值迭代
那么，如何为每个状态分配合适的价值函数值呢？这又要通过一个迭代过程，从问题的最终求解反向地迭代得到初始状态的价值函数。
在强化学习中，有一个经典地求解价值函数的方式，这就是大名鼎鼎的Q-Learning。2015年Google Deep Mind就是把Q-Learning算法结合深度神经网络成功地创造出一个通用的游戏玩家，在100多款Atari游戏上取得瞩目的表现。
Q-Learning算法的核心又是和梯度反传算法非常相似的。其中价值迭代类似于梯度反传，它会沿着时间的反方向迭代。另一个则是根据Q函数正向的决策过程，它会沿着时间的正方向迭代，从而形成最终的行动策略。这就是标准的强化学习的做法。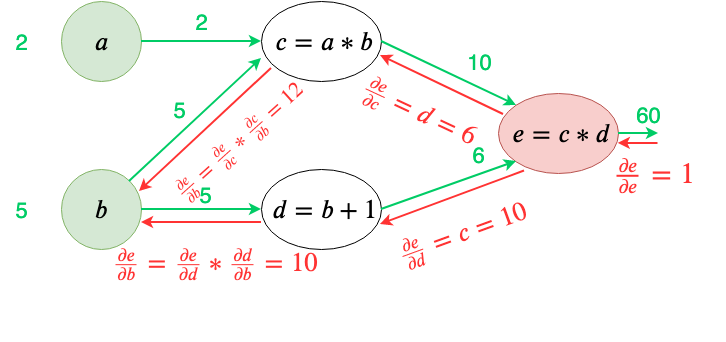
新年随笔：从《你一生的故事》到控制论梯度反传算法示意图
总结来看，无论是Q-Learning还是梯度反传，它们都涉及到一个双向对冲流的问题，如下图所示：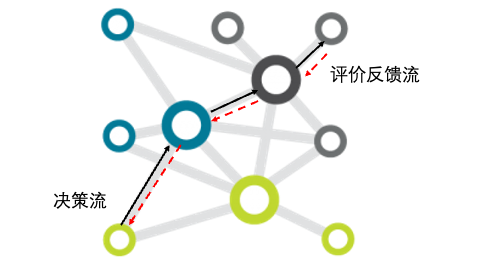

我们可以把任何一个复杂系统，无论是多个神经元构成的神经网络还是多个状态合成的复杂决策问题，都看作是一个相互连通的网络。其中，在网络上存在着两个相互几乎相反的流动，一个是沿着时间超前的“决策流”，另一个是沿着时间反传的“评价流”。
从抽象的“双向对冲流”的视角理解复杂适应系统的好处，是可以在更加底层的角度把握住各类学习系统的本质；其次，可以在这种抽象层次上建立起各类不同学习适应系统的类比关系，从而可以将一个领域的知识平移到另一个领域上去。例如，我们是否能够根据误差反传思想，或动态规划思想来设计人类组织中的评价机制？或者，我们甚至有可能站在“双向流”的视角，改进并超越现有方法（例如反向传播算法），让学习优化变得更加高效。

为什么你要学习一下控制论？

在前面的文字中，我用一种随笔的方式给你展现了最优控制原理是如何从物理中的最小作用量原理之中衍生出来了，并且介绍了它又是如何应用到无穷深神经网络的训练之中的。最后又从最优控制问题的离散求解引出了动态规划、价值函数迭代，以至于强化学习。
事实上，最优控制和强化学习存在着非常深刻的联系。我们不妨参考Recht B的PPT和文章。他曾总结如下：新年随笔：从《你一生的故事》到控制论
这是Matlab工具箱中给出的二者的联系：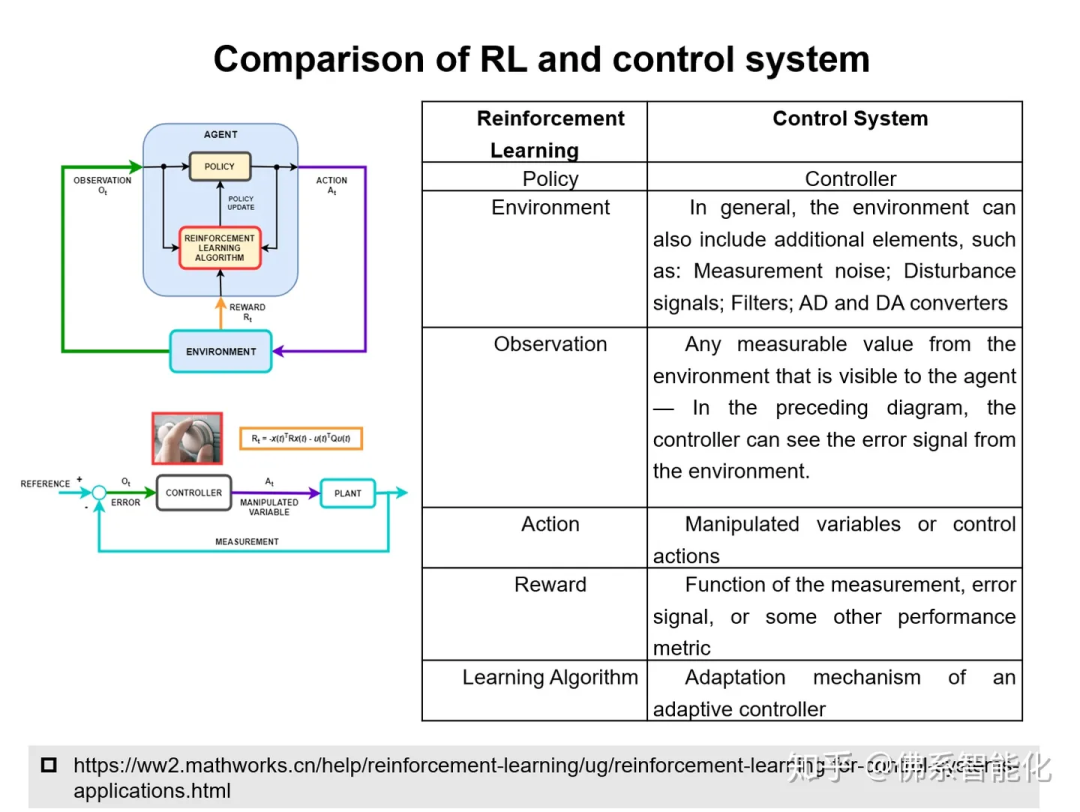

然而，最优控制问题只是控制论这门学问中的一小片花瓣。这里面的学问还有很多，因此也非常值得我们进一步深入学习。
你可能会质疑，控制论是最早起源于20世纪30年代的一门学问，已经非常古老了。而现在各式各样的深度强化学习算法早已经可以解决包括下围棋、打游戏等炫酷的任务了。
但我想说的是，首先，强化学习本身很多的创新源头也是来源于控制论的。另一方面，控制论（cybernetics），特别是后来发展起来的控制理论（control theory）基本上可以看作是一套数学。因此，它可以把各式各样的控制问题建模成最小的数学模型，从而方便你进行理论求解。这种能力可以让你一下子看到事物的本质。

这里所谓的控制论（cybernetics）是控制论的创始人维纳在二十世纪中叶提出的一门综合性学科。它实际上类似于今天的复杂科学，几乎可以是包罗万象的。它可以看作是今天的人工智能、决策科学、认知科学等思想的源头之一。

Cybernetics is a field of systems theory that studies circular causal systems whose outputs are also inputs, such as feedback systems. It is concerned with the general principles of circular causal processes, including in ecological, technological, biological, cognitive and social systems and also in the context of practical activities such as designing, learning, and managing.

另一方面，控制理论（control theory）是从控制论发展出来的一个专门的应用数学分支。它为如何控制一个动力系统提供了扎实的数学理论基础。

Control theory is an interdisciplinary field of engineering and mathematics that deals with the control of dynamical systems in engineered processes and machines.

那你可能困惑了，既然控制论这么重要，那我应该上哪去学呢？当然是集智学园新开的这门课——《控制科学前沿理论与方法》了！

控制科学前沿理论与方法系列课程

对复杂动态系统的定量认识与科学调控，系统学与控制论是关键基础。集智学园联合中科院数学与系统科学研究院多位控制科学与工程领域专家共同开设了《控制科学前沿理论与方法》系列课程，为面向控制专业领域学生以及跨领域的学习者做深度科普，帮助学习控制论的核心思想、框架与方法。通过学习这些课程，学生将了解控制论的发展历程，掌握经典和现代控制方法，探索控制系统的美妙之处。此系列课程共计10节，从2024年4月2日起，每周二晚19:00-21:00线上上课。欢迎感兴趣的朋友报名参与！