

关键词:参数化脉冲,互文子空间方法
导 读
本文是发表在 DAC 2024 上的论文 SpacePulse: Combining Parameterized Pulses and Contextual Subspace for More Practical VQE 的详细解读。该项研究由北京大学李彤阳课题组与圣母大学史弋宇教授课题组等合作完成,圣母大学博士生梁之鼎为第一作者,北京大学元培学院本科生杨睿为共同一作。论文提出了一种结合参数化脉冲和互文子空间的新方法,旨在提高变分量子本征求解器的实用性和效率,节省量子资源。


← 扫码跳转论文
论文地址:
https://arxiv.org/abs/2311.17423
01
引 言
量子计算具有解决传统计算机无法处理的部分复杂问题的潜力,然而其物理实现面临诸多挑战。特别是在含噪声中等规模量子(NISQ)时代[1],短的相干时间、有限的量子比特连接性以及高噪声水平限制了量子电路的大小和量子比特间的有效操作。为了应对这些挑战,研究者提出了变分量子算法,其中变分量子本征求解器(VQE)就是一个广泛研究的典型例子[2]。VQE 采用浅层、参数化的量子电路,使用经典的优化器更新电路参数,用于估计基态能量或期望值。尽管 VQE 具有适应噪声等优势,它也遇到了自身的一系列挑战,例如高量子资源需求,这些阻碍了其在近期量子设备上的可扩展性和准确性。为了提高 VQE 的实用性,一种可能的方法是利用变分脉冲电路[3],从门电路到脉冲电路的转变可以有效降低电路延迟。在当前的超导量子计算中,其应用越来越广泛,例如 IBM 公司专门推出了 IBM Qiskit Pulse 用以支持变分脉冲电路的实现[4]。
在本文中我们将互文子空间方法与脉冲电路整合,提出 SpacePulse 框架,有效地减少了所需量子比特的数量、测量次数以及整体电路深度,从而减少执行时间并降低量子资源开销,提高 VQE 在当前量子硬件上实现的可行性。
02
预备知识
1. 变分量子本征求解器(Variational Quantum Eigensolver):该算法使用加权的泡利算符来表示系统的哈密顿量,一个实现的关键部分是拟设(ansatz),即具有可调节参数的量子电路,用于准备哈密顿量的基态,对其测量我们可以确定系统基态能量的上界。VQE 的优势在于其迭代性质,通过量子态准备和经典优化结合不断更新拟设参数,每次迭代都更接近系统的最低能量配置,从而最小化哈密顿量的期望值。
2. 互文子空间方法(Contextual Subspace Method):互文子空间方法[5]将哈密顿量分为非互文(non-contextual)与互文(contextual)部分,量子互文性体现了测量结果与具体测量集选择的依赖关系,前者可以通过经典方法高效地近似,后者则在量子处理器上进行计算以修正最终结果。相较于用 VQE 直接计算原问题,这种方法可以有效减少所需的量子比特和测量次数。
3. 参数化脉冲拟设(Parameterized Pulse-based Ansatz):量子脉冲电路[6]是比量子门更为底层的实现层级。在超导量子计算机中,脉冲控制的关键参数包括脉冲振幅、角度、频率和持续时间,调整这些参数会直接影响驱动哈密顿量,进而作用于量子态的演化,具体如下式所示:
其中 代表振幅, 和 是由角度控制的相位参数, 为量子比特频率, 是驱动频率。
03
算法框架
SpacePulse 的核心在于将互文子空间方法与参数化量子脉冲结合,不同于其他模型通常采用基于门的电路拟设来构建能量估计的量子态,这种方法允许更直接灵活地操纵量子系统,减少电路复杂性,削减短相干时间对运行效果的负面影响,实现对量子硬件的更有效使用。算法框架如下图所示:
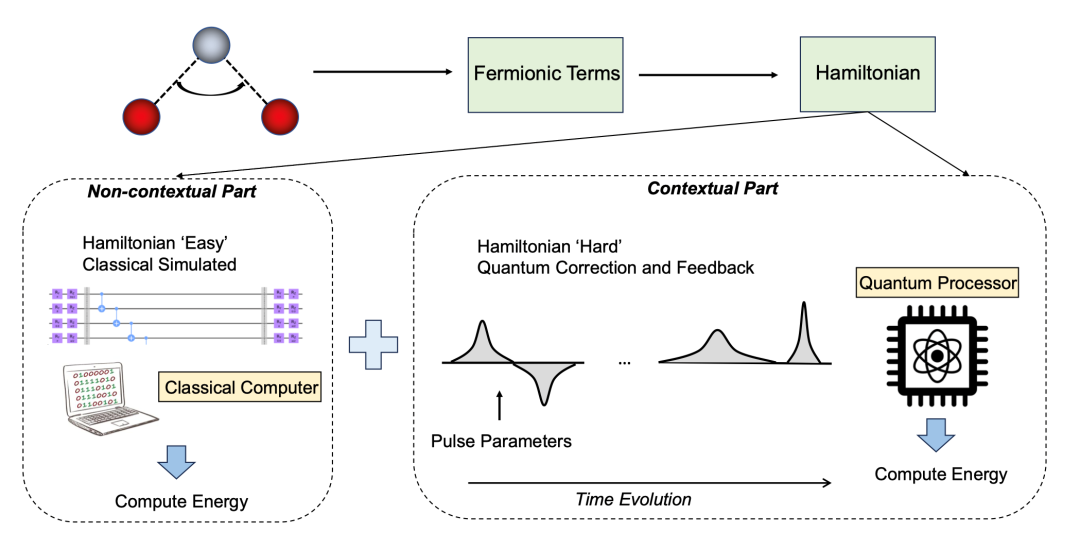
一方面,利用互文子空间方法,将分子哈密顿量分为“非互文”和“互文”两个部分[7]:“非互文”部分较为简单,可以为所有泡利项进行并发测量和联合值分配而不出现矛盾,可直接使用经典计算机高效处理;“互文”部分因涉及更多的量子特性,经典近似较为困难,故采取量子硬件上的高效拟设计算。通过混合经典-量子框架,有效平衡经典计算和量子计算的优势,提高效率。此外,运用以下技术降低整体的电路数量及大小,提升实用性。第一点处理是削减(Tapering)过程,其主要目的是减少量子比特的数量。该过程从分子哈密顿量中识别 Z2 对称性这种特殊模式,根据一对量子比特之间的关系,使用其中一个预测对系统状态的整体贡献,从而有效地移除冗余的量子比特。第二点采用泡利分组(Pauli Grouping)策略,对哈密顿量中对易的保利算符进行分组,可以实现多个算符的同时测量。一个简单的例子是,算符 XIXI、IXIX 和 IIXX 可以通过构建 XXXX 的电路同时进行测量。这种方法减少了所需的测量次数,显著加速测量过程。
另一方面,SpacePulse 模型对量子硬件上计算的哈密顿量“困难”部分使用了参数化脉冲拟设,使量子系统从其初始状态可以高效演化到所需的基态。与传统的门级电路不同,使用量子脉冲可以探索希尔伯特空间中那些通过传统的 CNOT 基础电路分解不易到达的区域。在 NISQ 阶段,脉冲级控制通常比同一搜索空间的门级控制更接近希尔伯特空间,直接操纵量子脉冲还允许我们避免依赖中间门表示,这些对于变分算法格外有用。利用这种脉冲级方法,可以缩短电路的持续时间,同时保持较高的准确性。
04
实 验
我们开展了一系列实验,以验证 SpacePulse 模型的效果。评估标准包括量子资源需求(量子比特、测量次数),执行时间以及能量估计的准确性。
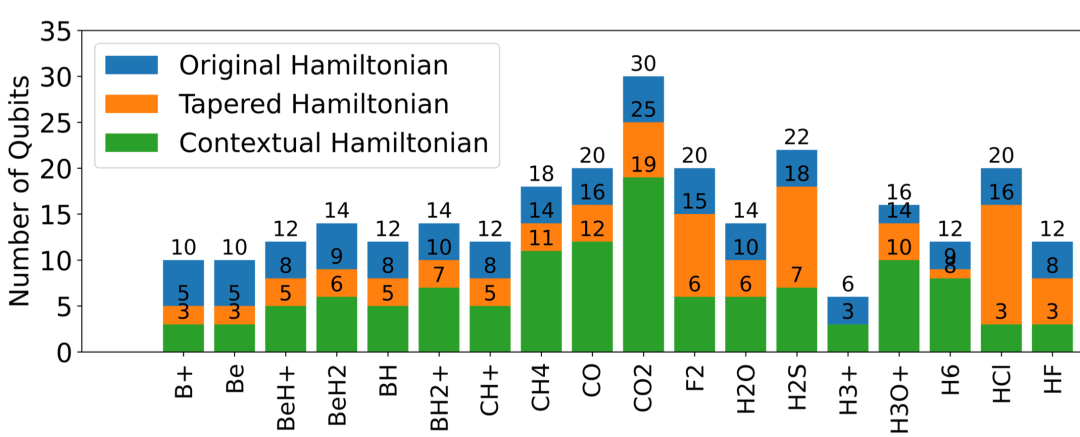
图2总结了将削减过程和互文子空间方法应用于电子结构哈密顿量的结果,如图所示(完整图片见论文),经处理后为实现化学精度(Chemical Accuracy)所需的量子比特数显著减少,极大地节省了量子资源。
下图展示了在一组哈密顿量上应用泡利分组策略后所需测量次数的对比结果。我们观察到,对于小任务(如 )测量次数可以从16减少到6,对于较大任务(如 )则可以减少超过100次测量。
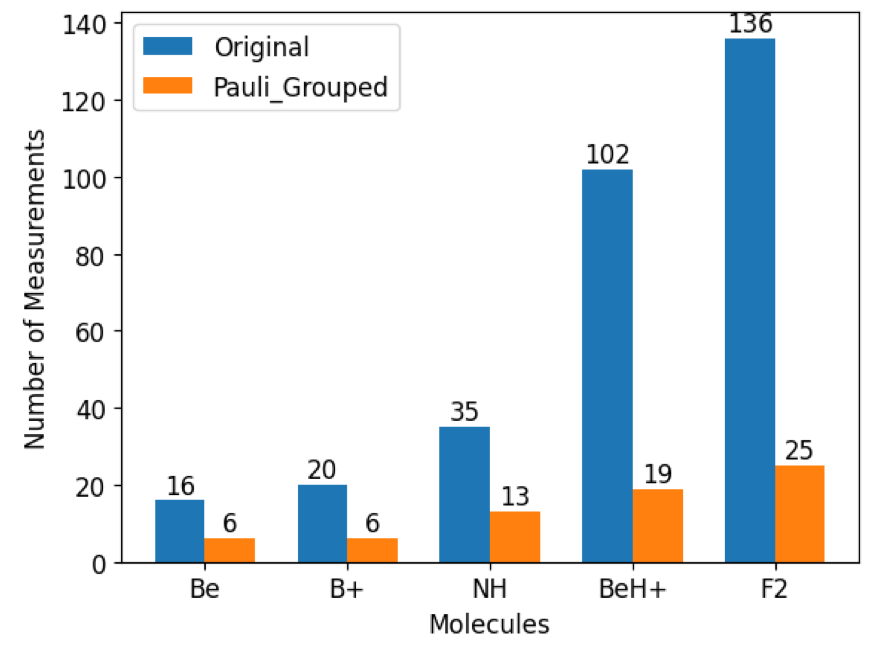
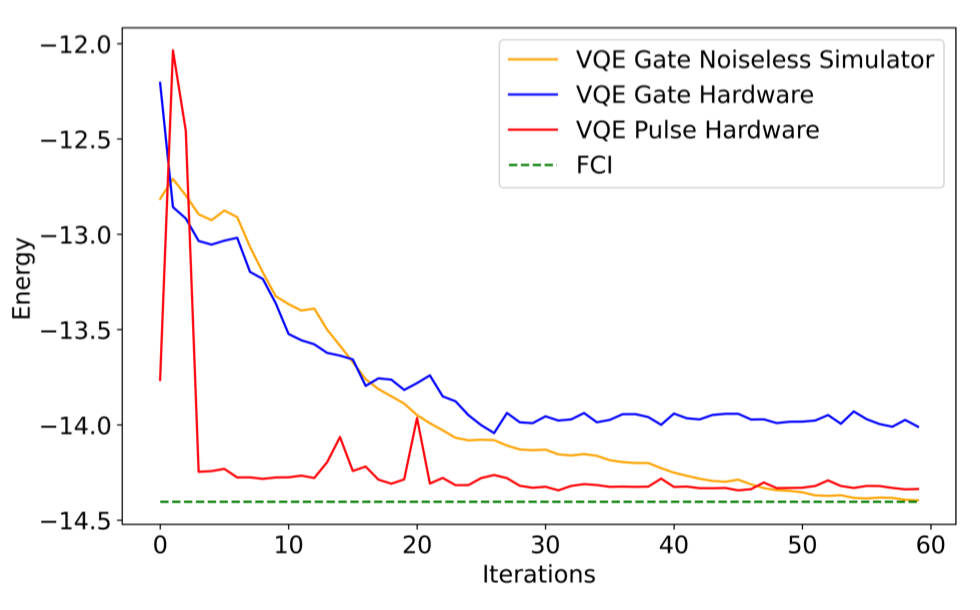
图5比较了在无噪声模拟器和真实硬件(ibmq_kolkata)上使用门级拟设,和在 ibmq_kolkata 上使用脉冲拟设对 分子的能量估计结果。所采用的门拟设是 EfficientSU2,这是一个经过验证的用于 VQE 任务的硬件高效拟设。相比之下,脉冲拟设将电路持续时间降低了81.82%,并实现了相同任务的更高精度(脉冲拟设在 ibmq_kolkata 上的精度为99.7%,门拟设为97.364%)。
即使我们将动态解耦(Dynamic Decoupling)应用到量子门拟设,脉冲拟设的表现仍具有可比性。我们选取了 、 、 和 分子作为测试案例。结果显示,脉冲拟设不仅保持了高精度,且在电路持续时间上显著改进,如在 上取得了更好的精确度和7.31倍的时间加速,体现了这种方法的优越性。此外,对动态解耦的量子门拟设应用零噪声外推(Zero-Noise Extrapolation)等错误消除(Quantum Error Mitigation)技巧可以进一步提高精确度,同样的方法也可以运用到脉冲拟设上,以取得更好的结果。
05
结 论
本文提出了一种优化 VQE 算法以便在近期量子硬件上更实用的新方法,通过将参数化量子脉冲拟设与互文子空间方法结合,在保持能量估计高准确性的同时显著减少量子资源需求。在 IBM Quantum Kolkata 等平台上进行的实验显示,SpacePulse 在模拟分子系统方面表现出较传统基于门的 VQE 方法的优势,特别是在减少量子比特和测量次数、缩短电路深度及执行时间方面。这些成果展示了 SpacePulse 的潜力,对于促进更实用有效的量子计算、解决广泛的应用问题有积极意义。
参考文献
[1] Preskill, John. “Quantum computing in the NISQ era and beyond.” Quantum 2 (2018): 79.
[2] Tilly, Jules, Hongxiang Chen, Shuxiang Cao, Dario Picozzi, Kanav Setia, Ying Li, Edward Grant et al. “The variational quantum eigensolver: a review of methods and best practices.” Physics Reports 986 (2022): 1-128.
[3] Liang, Zhiding, Hanrui Wang, Jinglei Cheng, Yongshan Ding, Hang Ren, Zhengqi Gao, Zhirui Hu et al. “Variational quantum pulse learning.” In 2022 IEEE International Conference on Quantum Computing and Engineering (QCE), pp. 556-565. IEEE, 2022.
[4] Alexander, Thomas, Naoki Kanazawa, Daniel J. Egger, Lauren Capelluto, Christopher J. Wood, Ali Javadi-Abhari, and David C. McKay. “Qiskit pulse: programming quantum computers through the cloud with pulses.” Quantum Science and Technology 5, no. 4 (2020): 044006.
[5] Kirby, William M., Andrew Tranter, and Peter J. Love. “Contextual subspace variational quantum eigensolver.” Quantum 5 (2021): 456.
[6] Egger, Daniel J., Chiara Capecci, Bibek Pokharel, Panagiotis Kl Barkoutsos, Laurin E. Fischer, Leonardo Guidoni, and Ivano Tavernelli. “A study of the pulse-based variational quantum eigensolver on cross-resonance based hardware.” arXiv preprint arXiv:2303.02410 (2023).
[7] Kirby, William M., and Peter J. Love. “Classical simulation of noncontextual Pauli Hamiltonians.” Physical Review A 102, no. 3 (2020): 032418.

图文 | 杨睿
PKU QUARK Lab
关于量子算法实验室
量子算法实验室 QUARK Lab (Laboratory for Quantum Algorithms: Theory and Practice) 由李彤阳博士于2021年创立。该实验室专注于研究量子计算机上的算法,主要探讨机器学习、优化、统计学、数论、图论等方向的量子算法及其相对于经典计算的量子加速;也包括近期 NISQ (Noisy, Intermediate-Scale Quantum Computers) 量子计算机上的量子算法。
实验室新闻:#PKU QUARK
实验室公众号:
课题组近期动态


— 版权声明 —
本微信公众号所有内容,由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料,版权属北京大学前沿计算研究中心微信所有;从公开渠道收集、整理及授权转载的文字、图片和音视频资料,版权属原作者。本公众号内容原作者如不愿意在本号刊登内容,请及时通知本号,予以删除。

点击“阅读原文”转论文链接



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


