合约广告中基于风险约束的Pacing算法优化

630次阅读

摘要：本文提出一种适用于合约保量广告的预算平滑Pacing算法，该算法通过对偶出价因子的百分位位置联动调控Pacing，兼容保量分配机制的同时，有效控制了预算释放过快的风险，并且最大程度兼顾了投放效果的提升。基于该项工作整理的论文已发表在AAAI’24，欢迎阅读交流。

论文：Percentile Risk-Constrained Budget Pacing for Guaranteed Display Advertising in Online Optimization

下载（点击↓阅读原文）：https://arxiv.org/abs/2312.06174

一、背景介绍

1.1 业务场景

合约广告（Guaranteed Delivery，GD）是通过合同形式，为品牌或直播广告主在指定时间内，在圈定的目标人群上触达确定数量的曝光。和效果广告的实时竞价相比，GD 广告采用曝光的合同固定价格计费，并且具有强保量的约束，也是广告主在大促时期确定性获取流量的重要广告形式。合约广告的在线分配机制中，通常基于「对偶理论」，采用”虚拟出价”（如 bid=CTR-对偶）的方式进行流量优选（0价过滤）和分配（最高价竞得），在满足保量约束的前提下，最大限度优化投放效果。除了合约广告，有很多场景有采用类似的建模方式，如：

push次数有限的情况下，最大化用户点击次数等；
消费券数量有限情况下，最大化转化率/成交uplift。

1.2 分配建模

假设我们以优化 CTR 为目标，对于第次请求召回的广告的预估价值为，原问题可以建模成：

根据原始对偶可以推导出，虚拟出价公式为：

其中是根据广告消耗速度的快慢，基于反馈算法（如PID等）进行调整得到的。虚拟出价后，再通过 0 底价过滤和出价排序，最终选取top1广告返回，过程表示为：

合约广告中基于风险约束的Pacing算法优化

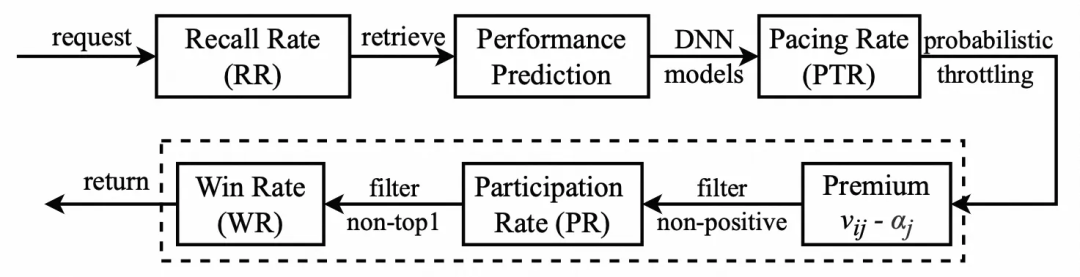
其中，表示召回率，表示Pacing模块的随机通过率，表示参竞率，表示竞得率。因此，一段时间内广告的曝光计费次数，可以串行漏斗来表示：

1.3 平滑问题

虽然理论上原始对偶方法可以实现最优的在线分配，但是在实际投放过程中，我们面对的是一个动态分配问题。如果只使用“虚拟出价”，非常容易出现不平滑的情况。比如，对偶因子初始值不合理，广告可能在几分钟之内释放完一个小时的预算；另外，PID反馈调整的步长设置不合理，也可能导致广告从完全没展现到瞬间“爆量”。不平滑释放会带来两方面问题：

1）业务方面：广告主希望预算均匀消耗，尤其是主播希望均匀引流，长时间无量或者爆量会带来客诉和资损；

2）效果方面：对广告感兴趣的用户是随着大盘流量均匀到达的，不平滑投放会浪费后续投放到优质流量的机会，对效果有损。

二、技术挑战与算法思路

2.1 现有算法

现有广告里平滑投放算法，主要有三类可以借鉴：

Bid Modification（出价修改）：相当于没有Pacing模块，通过参竞率来间接实现，反馈速度慢且对于小订单风险巨大（如初始值不合理预算瞬间花完），达不到较好的预算平滑效果
Probabilistic Throttling（概率节流）：简单高效，在RTB使用广泛，但是在合约广告里，直接使用会带来一个问题，同时用一个信号（预算消耗速度）反馈调整两个参数（出价&Pacing），会出现相互干扰、控制混淆，引起保量风险和平滑问题。举个例子，广告释放过快，应该调低出价，还是调低Pacing通过率？
Regularization（分配正则项）：在之前合约分配模型建模常采用正则项，以实现平滑或者均匀分配，但是这种方法的正则项超参数是固定的，无法在投放中自适应调整。

综上，现存的方法并不能很好解决我们的问题。

2.2 合约业务挑战

分析我们业务里面平滑释放的挑战，主要包含以下因素：

1）静态因素

预定量：不同广告的保量目标从几千到几百万PV不等
定向：不同广告的定向人群、定向资源位不同
优化目标：不同广告优化目标不同（转化率/停留时长/进店率等），不同类型的目标分布差异极大，如转化率~0.1%，点击率~10%，仅打分的平均值就相差百倍，导致调控的初始化和步长配置非常复杂

2）动态因素

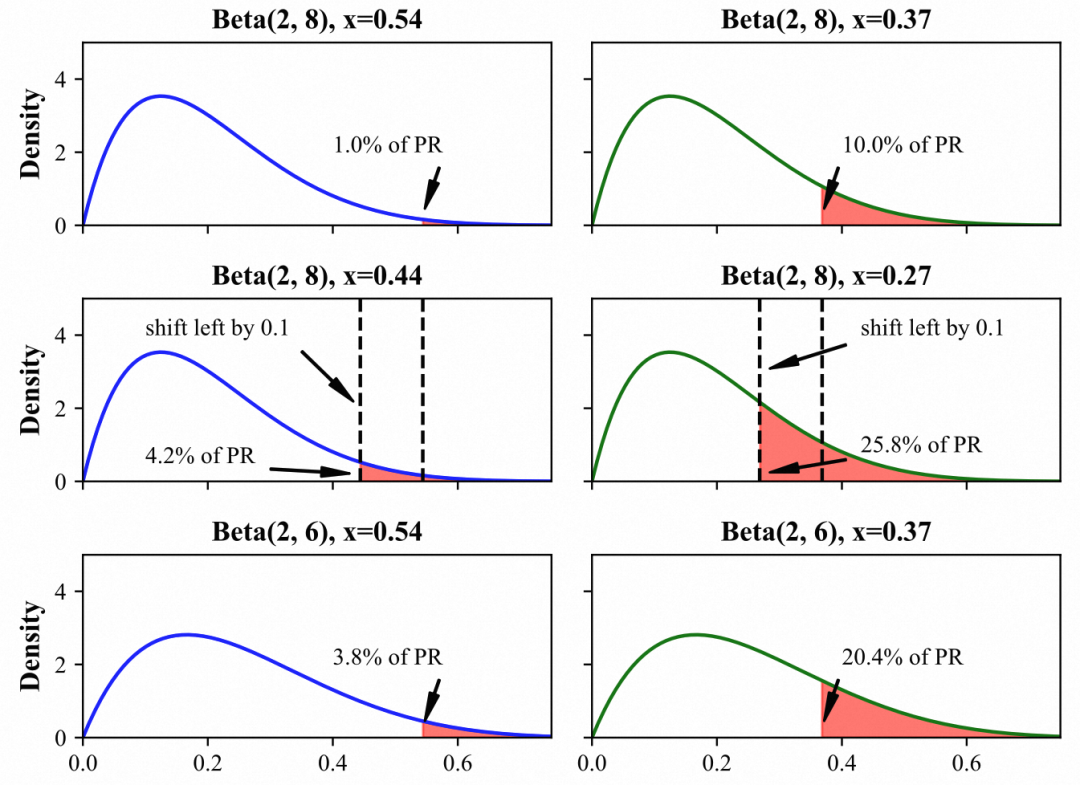
假设有两个广告 Ad1 和 Ad2，除了 Ad1 的流量供给大很多，其他静态因子都相同的情况下，最终收敛后 Ad1 的对偶因子一定高于 Ad2 的对偶因子。这意味着：

由于 Ad1 的流量供给大于 Ad2，Ad1 更容易“爆量”；
Ad1 的虚拟出价远低于 Ad2， Ad1 的竞得率更容易受其他订单的影响；
从参竞率的角度，如果对偶因子反馈调整相同距离，或者打分分布发生变化，Ad1 的波动也比 Ad2 更大，可以用下图来表示这个过程：

合约广告中基于风险约束的Pacing算法优化

2.3 算法设计思路

平滑投放的主要挑战来自于释放过快，因为消耗是无法回撤的，而释放过慢可以通过后期反馈进行调整后加速。设计合约广告中的Pacing算法，需要考虑以下几点：一方面通过 Pacing 随机通过率，来控制广告的流量供给，把对偶因子限制在安全的百分位范围内，避免由于调控出现参竞率太大的波动。另一方面，Pacing如果过滤流量太多，会让对偶因子处于较低百分位，虽然没有平滑风险，但是会随机丢弃大量优质流量，不利于效果提升。所以一个合格的合约Pacing算法，需满足以下三点要求：

1）不能破坏合约保量分配机制，不干扰到对偶因子的调控，否则有缺量风险；
2）能有效控制平滑风险（对偶百分位不能太高）；
3）尽量避免丢弃优质流量，减少效果损耗（流量充足情况下，对偶百分位不能太低）。

三、风险约束的Pacing算法细节

3.1 双向变换

为了解决不同打分类型分布不一致，导致“对偶初始化”以及”调控步长“难以统一设置的问题，一个很简单的思路，是将所有打分通过之前落盘打分日志，统一变换到 [0,1] 的均匀分布。但是这带来的问题是，我们的求解目标从变成了。尽管百分位变换是保序，但是其非线性变换的特性，将导致百分位空间的最优解并不是原问题的最优解（不同类型分数，竞得率的公平性不在讨论范围内）。基于此，我们采用了双向变换：

1）效果分前向变换：原空间() => 百分位()，将打分映射到百分位空间，在百分位空间调整对偶。通过对偶在百分位空间的位置，可以感知爆量风险（比如当前对偶调整到 0.99，说明参竞率为1%，爆量风险较高），并在pacing策略采取对应调整措施约束风险；

2）对偶后向变换：百分位() => 原空间()。在百分位空间调整对偶后，反向变换到原空间，所以bid 的计算还是在原来的空间，保证我们求解的是原问题的最优解。

原空间到百分位空间的变换，可以基于非参数方法（如累计直方图统计），也可以采用参数化方法变换。这里我们采用了参数化的 BoxCox 方法，将原空间变换到正态分布，再通过标准化转换为标准正态分布，最后通过标准正态分布的累积分布函数(CDF)，变换成0到1的均匀分布，即百分位空间。变换过程如下图所示：

合约广告中基于风险约束的Pacing算法优化

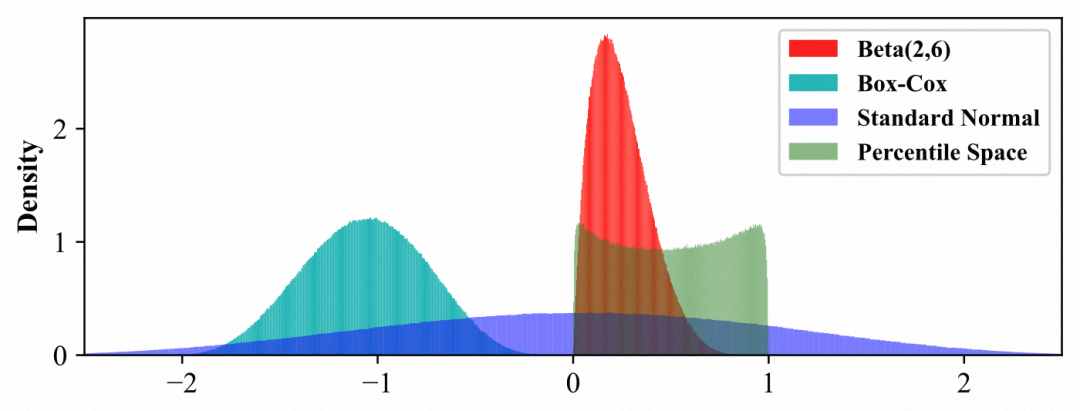
后向变换与上述过程正好相反，互为逆函数。

3.2 PTR粗估

上述我们分析了对偶的百分位越高，对应广告的参竞率越小，不平滑风险越高。因此我们希望 Pacing 模块通过随机通过功能，将每个广告的对偶的百分位限制在一个安全阈值内。例如表示期望收敛后，此时广告有top 5%的优质流量参竞，余下的 95% 流量bid为负被底价过滤。假设广告定向的人群大小为，全局的竞得率为，通过之前的流量漏斗公式，可以粗估出Pacing的通过率()为：

百分位对偶值初始化可以表示为：

3.3 PTR微调

尽管我们在离线对 PTR 进行了粗估，但是在实际投放过程中，粗估值和实际线上投放情况可能有较大误差，因此需要根据线上情况进行微调。微调函数我们分解为两个函数：

1）对偶联动

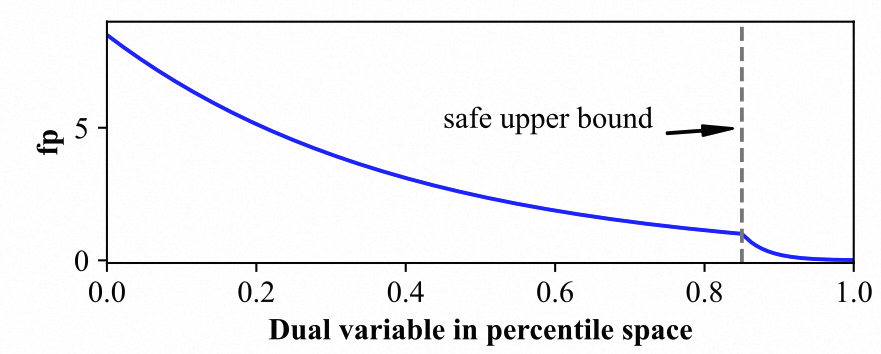
在线实际投放中如果，说明偏小，需要增加流量供给，减少缺量风险和优质流量损耗；反之则说明偏高，需要快速降低以约束风险，我们用两段指数函数来进行微调：

函数如下图所示：

合约广告中基于风险约束的Pacing算法优化

2）出价加权

受到 smart pacing 论文的启发，效果越好的流量，PTR 应该更高。对应到我们的算法中，对于同一个广告来说，即 bid 越高通过率越高。如果用原空间的bid加权，由于广告的打分分布差异很大，bid也有很大的差异，不利于统一设置加权倍率。因此，我们在百分位空间进行加权，这里我们采用简单的线性加权，即：

如下图所示：

合约广告中基于风险约束的Pacing算法优化

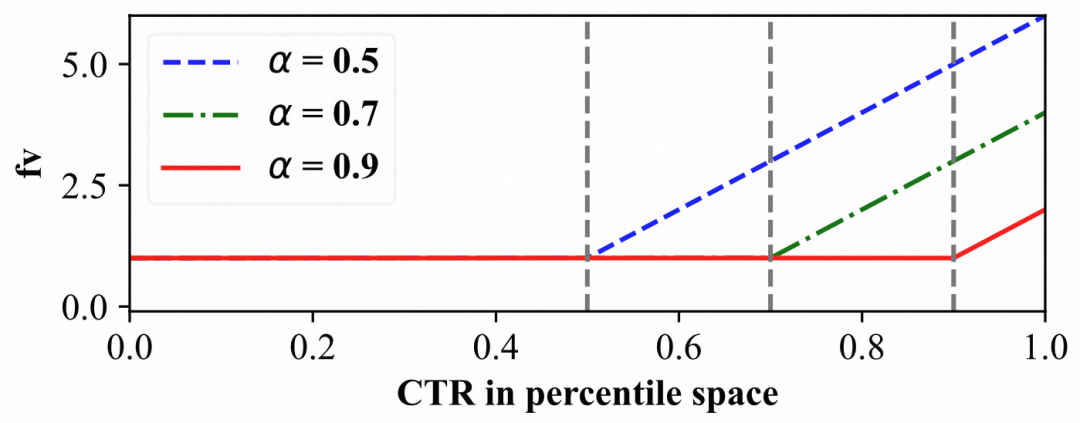
相比于，是根据在线实时的“虚拟出价”进行加权的，是完全实时自适应的。举个例子，比如我们归一化参数更新不及时或者计算有偏差，导致变换后的打分分布是的均匀分布，对于函数来说，会在离线粗估的 PTR的基础上添加较大的倍数，存在爆量的风险，而对于函数来说则不存在这样问题。

3.4 梯度裁剪

在 PID 反馈调控算法中，如果步长太大，调控容易出现大幅抖动，如果太小反馈调整的反应速度又太慢。一种常见的做法是静态梯度裁剪。假设限制相邻两次调整的对偶调整最大距离为，通过 PID 算法计算出下一次百分位空间的对偶因子的值为 , 则下一次百分位对偶变量更新值为：

这种做法的一个缺点是，对偶因子在不同的百分位位置调整，带来的波动其实是不一样的。如百分位对偶从0.9 调整到 0.8，参竞率（PR）可以从 0.1 增加到 0.2出现翻倍现象；百分位对偶从 0.2 调整到0.1，PR 则仅从 0.8 增加到0.9，几乎没有变化。上述只分析了百分位对偶调整对于参竞率的影响，此外，百分位对偶的调整还会影响到 PTR 和 WR。以下推导基于广告出现缺量情况：根据反馈算法将往下调。假设该广告的召回率、打分分布、在线竞价环境在这期间没有发生变化，会发生以下变化：

会增加。竞价环境不变，下调对偶会提升 bid ，top1排序概率变大；
会增大。随着下调提高加权倍率；
也会增大。下0 底价过滤的比例也会降低。

假设我们广告在第次周期中的真实消耗是，期望消耗是，则释放速度可义为：

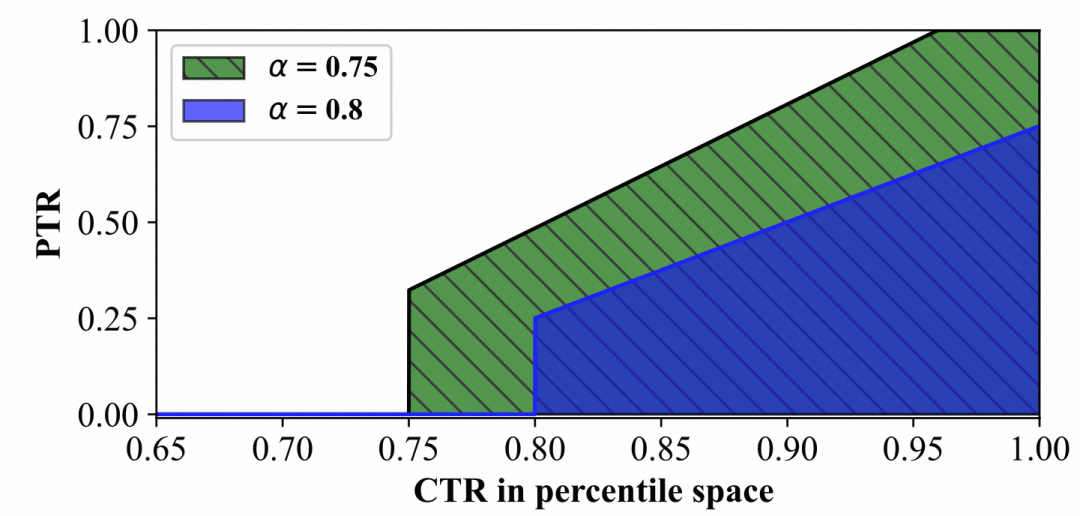
理想的调控结果是让轮的消耗速度为1。上面分析了 WR、PTR 和 PR 都会增加，由于竞价环境是未知的，增加倍率无法计算，但是如果增加到了倍，那么广告在轮的释放速度肯定就超过 1 了，这就是我们调整范围的下限。定义函数：

实际求解时，可以通过蒙特卡洛重要性采样的方法进行积分计算。具体做法是：随机在有颜色区域的轴上打1000个点得到平均高度，乘以宽度就即为。然后用二分查找法找到的下限：下图表示函数：

合约广告中基于风险约束的Pacing算法优化

在线上实际使用时，我们采用的是静态 + 动态梯度裁剪的方法双管齐下来控制风险：

3.5 可变步长

梯度裁剪只是限制了更新的上限和下限，实际的更新的步长也有较大的优化空间。直觉上，越靠近 1，PR 波动越大，此时步长应该越小；反之越靠近 0，PR 波动越小，不平滑的风险也更小，步长也应该设置更大。这个直觉上的判断，可以通过数学推导得到一个可变更新步长，详情可以查阅我们发表在 AAAI’24的论文：Percentile Risk-Constrained Budget Pacing for Guaranteed Display Advertising in Online Optimization (https://arxiv.org/abs/2312.06174，点击↓阅读原文↓)。

3.6 止血控制

以上所有的策略，都是基于梯度更新实现的。梯度更新有一个较大的问题是，当线上已经发生“爆量”情况，往往需要多次更新才能控制“险情”，这时候小时预算往往已经消耗完毕。针对这种情况，我们采用比例调控的方式，额外增加一个通用率进行及时止血，把广告的释放速度控制在2倍，既能防止损失进一步扩大，也能让对偶因子朝着正确的梯度方向进行逐步调整，止血调控的通过率计算公式为：

所以最终的的Pacing，由两个概率通过模块串行组成：

3.7 冷启问题

在广告刚上线的几分钟，止血通过率可以设置成 10% 进行小流量试探，防止对偶初始化不准确导致不平滑现象。

3.8 流量倾斜

在合约业务里，往往还有很多业务需求需要对部分流量进行加权投放，如通投广告主中需要对广告主圈选的人群进行流量倾斜、部分资源位流量倾斜等，可以从两方面进行干预：

Pacing 对需要倾斜的流量进行通过倍率加权，以增加 PTR；
Bid 环节对需要倾斜的流量进行出价加权，以增加 PR 和 WR。

如果流量倾斜需要达到某个目标，则加权因子需要通过反馈调节链路进行调整。

3.9 整体流程

总结起来，Pacing 算法的流程如下：

1）设置超参数

全局参数：安全百分位阈值，步长，静态梯度裁剪；
广告参数：预算，定向人群大小，止血冷启动通过率。

2) 离线计算

对于每个广告：根据供需比计算基础通过率；
计算分位对偶初始值；
根据广告优化目标的类型，通过历史日志统计对应目标类型的归一化参数（包括 boxcox参数、均值、标准差）。

3）在线决策

对于召回的广告列表：用 RTP DNN模型预估分数；
将打分转换到百分位空间；
将百分位对偶通过后向变换成原空间对偶；
计算原空间出价和百分位空间出价；
0 底价过滤；
通过、和计算通过率；
计算最终Pacing通过率；
以的概率保留广告；
按照原空间出价排序；
选取 Top 1 返回。

4）近线调控

每隔两分钟进行一次近线调控；
计算上次调控的释放速度；
根据PID 算法（或动态步长算法），计算本次百分位空间的对偶值；
通过蒙特卡洛重要性采样，计算动态梯度裁剪的上下界；
进行静态 + 动态梯度裁剪，得到更新后的百分位对偶；
根据释放速度，通过止血调控更新公式，得到止血通过率；
将和推送到线上，进行下一轮在线决策。

4. 业务效果

互动合约广告对平滑投放要求较高，算法侧经过一段时间的迭代和优化，逐步形成了以上基于百分位风险约束的Pacing策略，并通过了日常投放、双十一大促等各方面考验。在日常互动商业上场景上，我们对出价加权进行了消融实验，相比于无出价加权策略，收藏加购购买率及吸粉入会率均有所提升，平滑释放和效果提升达到了较好的平衡。

5. 总结

本文提出一种适用于合约保量广告的预算平滑Pacing算法，该算法通过对偶出价因子的百分位位置联动调控Pacing，兼容保量分配机制的同时，有效控制了预算释放过快的风险，并且最大程度兼顾了投放效果的提升。实验表明，该方案使平滑释放和效果提升达到了较好的平衡。