
作者 | Manish Gupta
OneFlow编译
翻译|宛子琳、杨婷
AI驱动的技术正逐渐融入人们日常生活的各个角落,有望提高人们获取知识的能力,并提升整体生产效率。语言大模型(LLM)正是这些应用的核心。LLM对内存的需求很高,通常需要专用的硬件加速器,以高效地提供数百亿亿次浮点运算(Exaflops级别)的计算能力。本文将展示如何通过更有效地利用内存来解决计算方面的挑战。
LLM中的大部分内存和计算资源都消耗在了矩阵乘法操作中的权重上。使用范围更小的数据类型可以降低内存消耗,例如,将权重存储为8位整数(即U8或S8)的数据类型,相对于单精度(F32)能够减少4倍的内存占用,相对于半精度(F16)或bfloat16(BF16)能够减少2倍的内存占用。
此外,先前的研究表明,LLM模型采用S8格式的权重和F16格式的输入进行矩阵乘法运算,能够在保持可接受的准确性的同时提高效率。这一技术被称为仅权重量化(weight-only quantization),需要对带有混合输入的矩阵乘法进行高效实现,例如半精度输入与8位整数相乘。因为硬件加速器(包括GPU)支持一组固定的数据类型,因此,混合输入矩阵乘法需要通过软件转换来映射到硬件操作。
为此,本文重点关注将混合输入的矩阵乘法映射到NVIDIA Ampere架构上。我们提出了解决数据类型转换和布局一致性的软件技术,以有效地将混合输入矩阵乘法映射到硬件支持的数据类型和布局上。结果显示,在软件中进行额外工作的计算开销很小,并且可以实现接近硬件峰值的性能。本文所介绍的软件技术已在开源的NVIDIA/CUTLASS库(github.com/NVIDIA/cutlass/pull/1084)中发布。
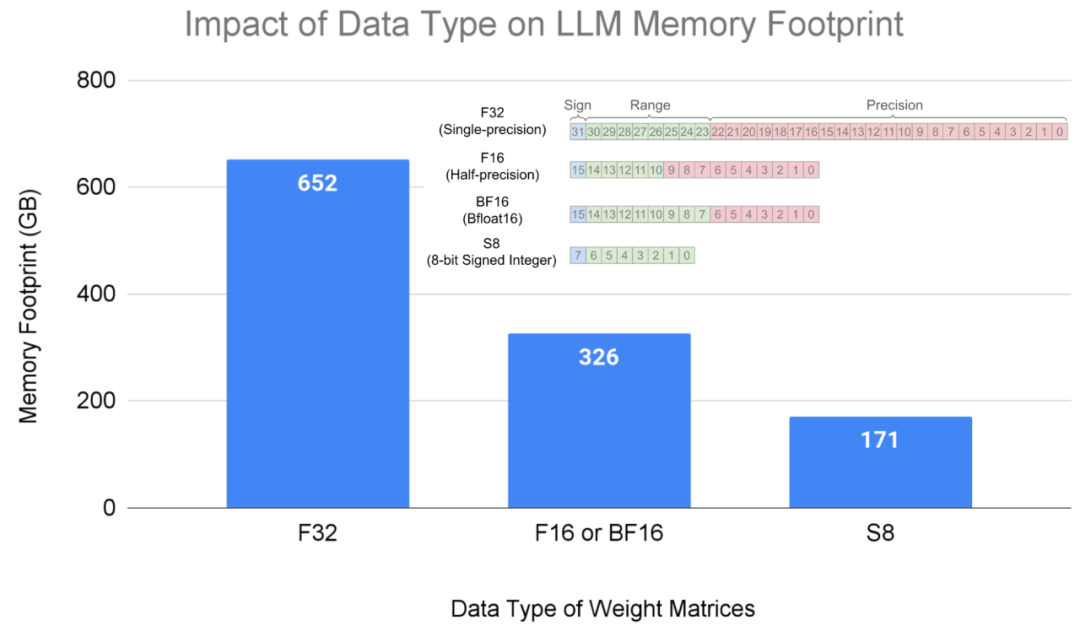
175亿参数的LLM模型在不同数据类型格式下的内存占用。
(本文作者为谷歌研究院高级软件工程师Manish Gupta。以下内容由OneFlow编译发布,转载请联系授权。原文:https://blog.research.google/2024/01/mixed-input-matrix-multiplication.html)
1
矩阵乘累加(matrix-multiply-accumulate)运算
当前的AI硬件加速器,如Google的TPU和NVIDIA的GPU,通过针对张量核心(Tensor Core)在硬件中本地执行矩阵乘运算(这些张量核心是专门加速矩阵运算的处理单元),尤其适用于AI工作负载。本文我们重点关注NVIDIA Ampere张量核心,它提供矩阵乘累加(mma)运算。在本文其余部分,mma指的是Ampere张量核心。在mma运算中,两个输入矩阵(称为操作数)所支持的数据类型、维度和数据布局在硬件中是固定的。这意味着,软件中不同的数据类型和更大维度的矩阵乘法是通过将问题划分为硬件所支持的数据类型、形状和布局实现的。
张量核心的mma运算通过指定两个输入矩阵(如下图所示的A和B)来计算生成结果矩阵C。mma运算本身支持混合精度。混合精度张量核心允许混合输入(A和B)数据类型与结果(C)数据类型。相比之下,混合输入矩阵乘法涉及混合输入数据类型,这在硬件上不受支持,因此需要通过软件实现。
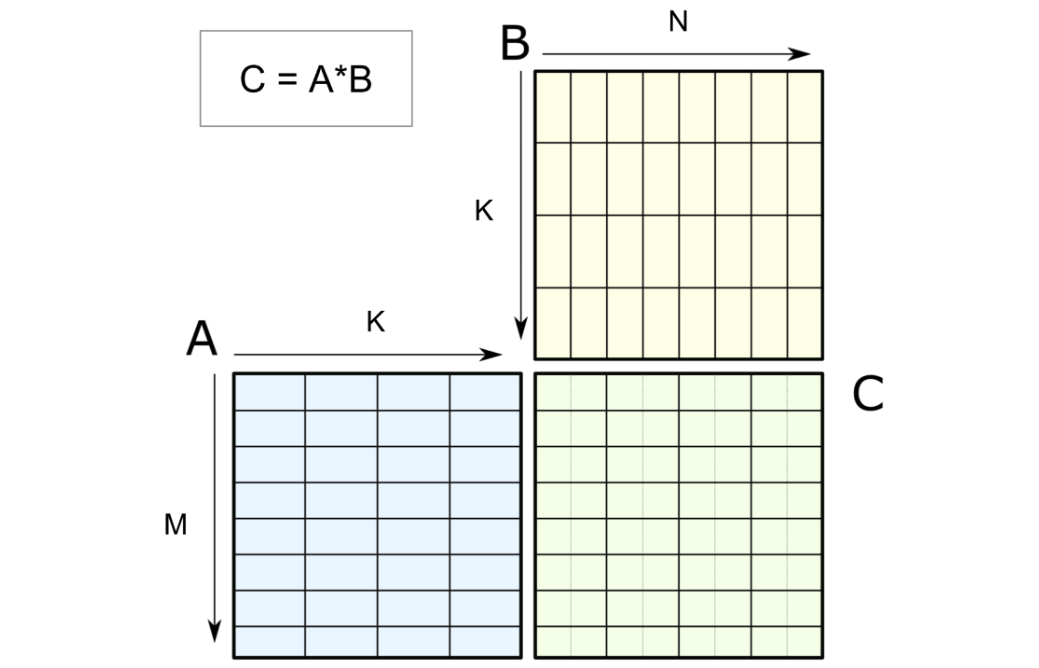
对M乘K的输入矩阵A和K乘N的输入矩阵B进行的M乘N乘K的张量核心操作,
得到M乘N的输出矩阵C。
2
混合输入矩阵乘面临的挑战
为简化讨论,我们选择了混合输入矩阵乘法的一个具体示例:用户输入采用F16,模型权重采用U8(表示为F16 * U8)。本文讨论的技术适用于各种混合输入数据类型组合。
GPU程序员可以访问一系列内存,包括全局内存、共享内存和寄存器,这些内存按容量递减但速度递增的顺序排列。NVIDIA Ampere Tensor Core的mma操作从寄存器中获取输入矩阵。此外,输入和输出矩阵需要符合在一个名为warp的32个线程组内的数据布局。对于mma操作,warp内支持的数据类型和布局是固定的,因此要高效实现混合输入乘法,就需要在软件中解决数据类型转换和布局一致性问题。
数据类型转换
mma操作要求两个输入矩阵具有相同的数据类型。因此,在混合输入矩阵乘法中,当一个操作数以U8存储在全局内存中,而另一个以F16存储时,就需要进行从U8到F16的数据类型转换。这种转换将两个操作数转换为F16,从而将混合输入矩阵乘法映射到硬件支持的混合精度张量核心。鉴于权重的数量庞大,因此需要大量的转换操作,我们的技术展示了如何降低其时延并提高性能。
布局一致性
mma操作还要求两个输入矩阵的布局(即在一个warp的寄存器中的布局)符合硬件规范。在混合输入矩阵乘法(F16 * U8)中,U8数据类型的输入矩阵B的布局需要符合转换后的F16数据类型。这被称为布局一致性(layout conformance),需要通过软件实现。
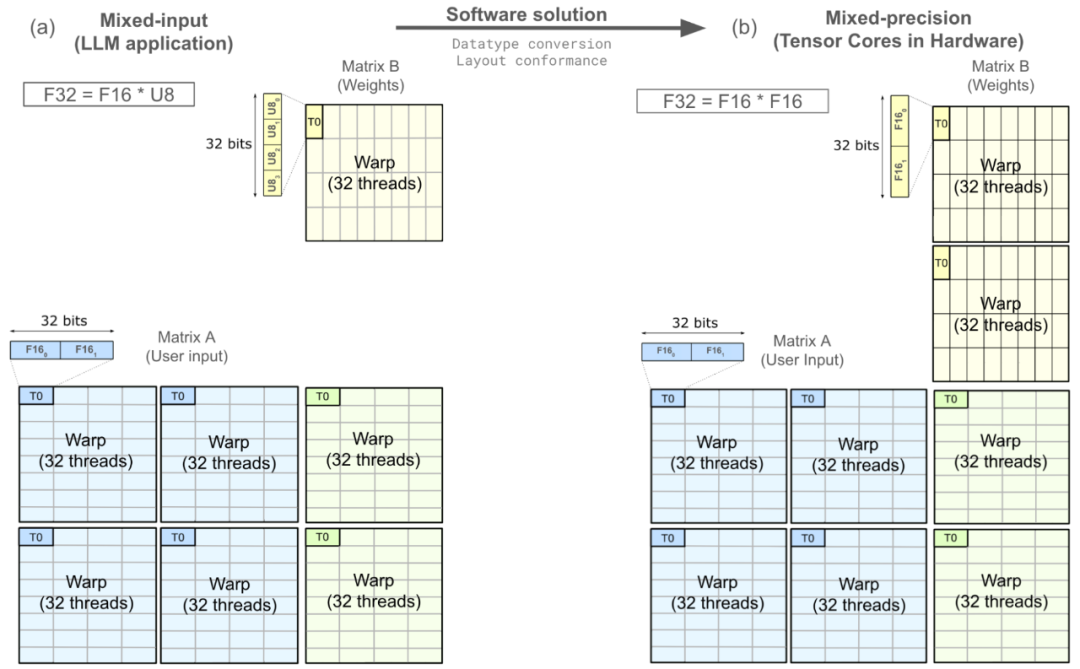
下图展示了一个mma操作,它从寄存器中提取矩阵A和矩阵B,然后在寄存器中生成矩阵C,这个过程分布在一个warp中。其中,线程T0被突出显示,并对其进行了放大,以展示权重矩阵B经过数据类型转换,需要符合布局一致性才能映射到硬件支持的张量核心操作。
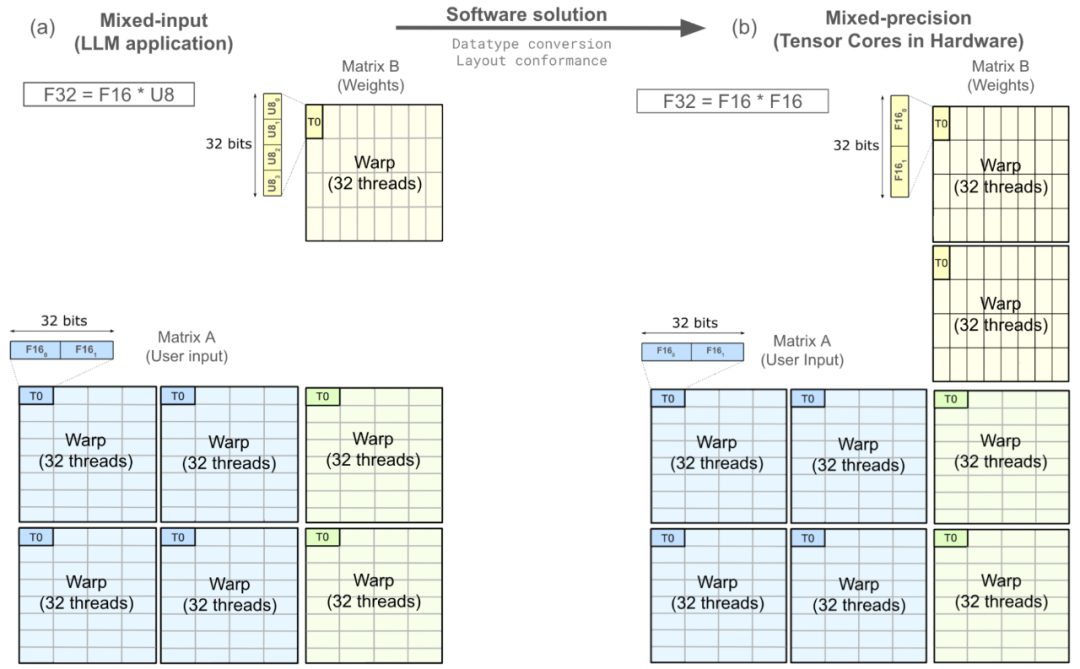
将软件中的混合输入(F32=F16U8)操作映射到硬件中原生支持的warp级张量核心(F32=F16F16)。原图来源:《在NVIDIA A100上开发CUDA核心以充分发挥张量核心的性能极限》。
2
应对计算挑战的软件策略
典型的数据类型转换涉及对32位寄存器的一系列操作,如下图所示。每个矩形块代表一个寄存器,相邻文本则表示相应的操作。整个序列展示了从4个U8转换为2个(2个F16)的过程。该序列大约包含10个操作。
在32位寄存器中,将4个U8转换为2x(2个F16)的NumericArrayConvertor。
实现布局一致性的方法有很多,两种现有解决方案如下:
1.较窄位宽的共享内存加载:在这种方法中,线程发出较窄位宽的内存加载操作,将U8数据从共享内存移动到寄存器。这会导致两个32位寄存器,每个寄存器包含2个F16值(如上所示,对于矩阵B的线程T0)。较窄的共享内存加载直接实现了布局一致性,使其存入寄存器,而无需任何移动(shuffles)操作;然而,这种方法未充分利用共享内存带宽。
2.全局内存中的预处理:另一种策略是,在全局内存中重新排列数据(在内存层次结构中位于共享内存的上一级),允许更宽的共享内存加载。这种方法最大程度地利用了共享内存带宽,并确保数据以一致的布局直接加载到寄存器中。虽然重新排列过程可以在LLM部署之前离线执行,确保不影响应用程序的性能,但它引入了一个额外的、有意义的硬件特定的预处理步骤,需要额外的程序来重新排列数据。
NVIDIA/FasterTransformer采用这种方法有效地解决了布局一致性的挑战。
3
优化的软件策略
为进一步优化并减少数据类型转换和布局一致性的计算开销,我们分别实现了FastNumericArrayConvertor和FragmentShuffler。
FastNumericArrayConvertor在32位寄存器中直接处理4xU8,而无需拆解单个1xU8值。此外,它使用的算术操作成本较低,减少了指令数量,提高了转换速度。
U8到F16的转换序列如下图所示。这些运算使用打包的32位寄存器,避免了显式的解包和打包。FastNumericArrayConvertor使用置换字节来重新排列4xU8的字节,将其放入两个寄存器中。此外,FastNumericArrayConvertor不使用开销较大的整数到浮点数转换指令,并采用矢量化操作,在两个32位寄存器中获取包含2x(2xF16)值的打包结果。相对于上述方法,U8到F16的FastNumericArrayConvertor大约使用了六个操作,相对上文提到的方式,其性能有约1.6倍的提升。
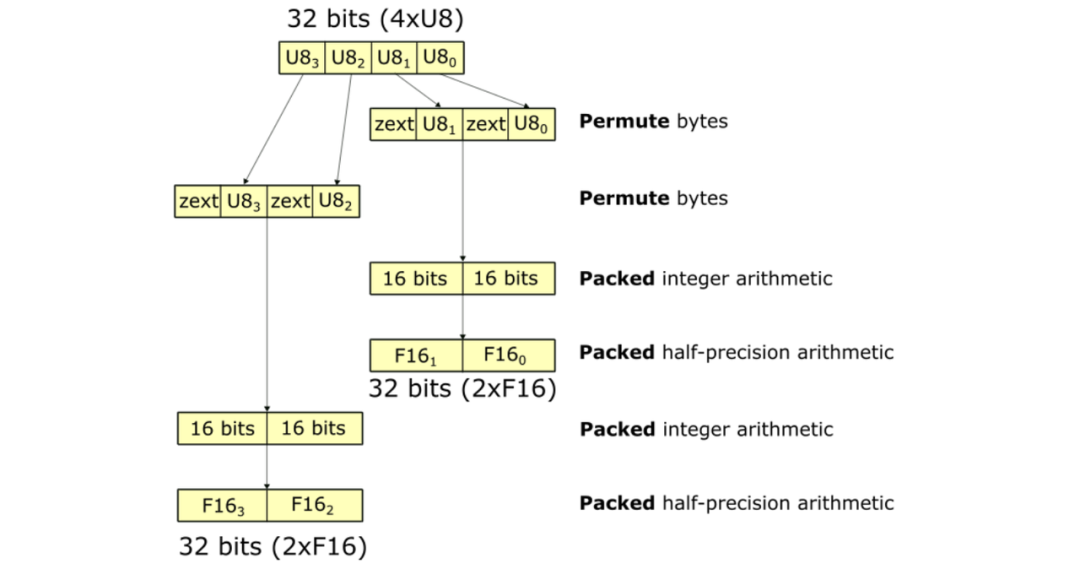
FastNumericArrayConvertor利用permute字节和packed计算,减少了数据类型转换中的指令数量。
FragmentShuffler通过对数据进行重新排列,可以使用更宽的位宽加载操作,实现了布局一致性,增加了共享内存带宽利用率,并减少了总操作数。
NVIDIA Ampere架构提供了一个加载矩阵指令(ldmatrix)。ldmatrix是一种warp级操作,其中一个warp的32个线程将数据从共享内存移动到寄存器中,而这些寄存器的形状和布局符合矩阵A和B进行矩阵乘法累积运算所需的要求。使用ldmatrix减少了加载指令的数量,提高了内存带宽利用率。由于ldmatrix指令将U8数据移动到寄存器中,加载后的布局符合U8U8的mma操作,不符合F16F16的mma操作。我们实现了FragmentShuffler,使用shuffle(shfl.sync)操作在寄存器内重新排列数据,以实现布局一致性。
这项工作最重要的贡献之一就是通过寄存器shuffles实现了布局一致性,避免了在全局内存中进行离线预处理或更窄的位宽共享内存加载。此外,我们提供了FastNumericArrayConvertor的实现,涵盖了从U8到F16、S8到F16、U8到BF16以及S8到BF16的数据类型转换。
4
性能表现
我们在NVIDIA A100 SXM芯片上测量了该方法的八种混合输入变体的性能(如下图中的蓝色和红色所示;根据矩阵A和B的数据类型不同而变化)以及两种混合精度数据类型(绿色显示)的性能。性能结果以FLOPS(数值越高表示性能越好))显示。
值得注意的是,相对于最后两个矩阵乘法,前八个需要额外的操作,因为混合精度变体直接针对硬件加速的张量核心操作,无需数据类型转换和布局一致性。即便如此,在混合输入矩阵乘法性能上,我们的方法仅略低于或与混合精度相当。
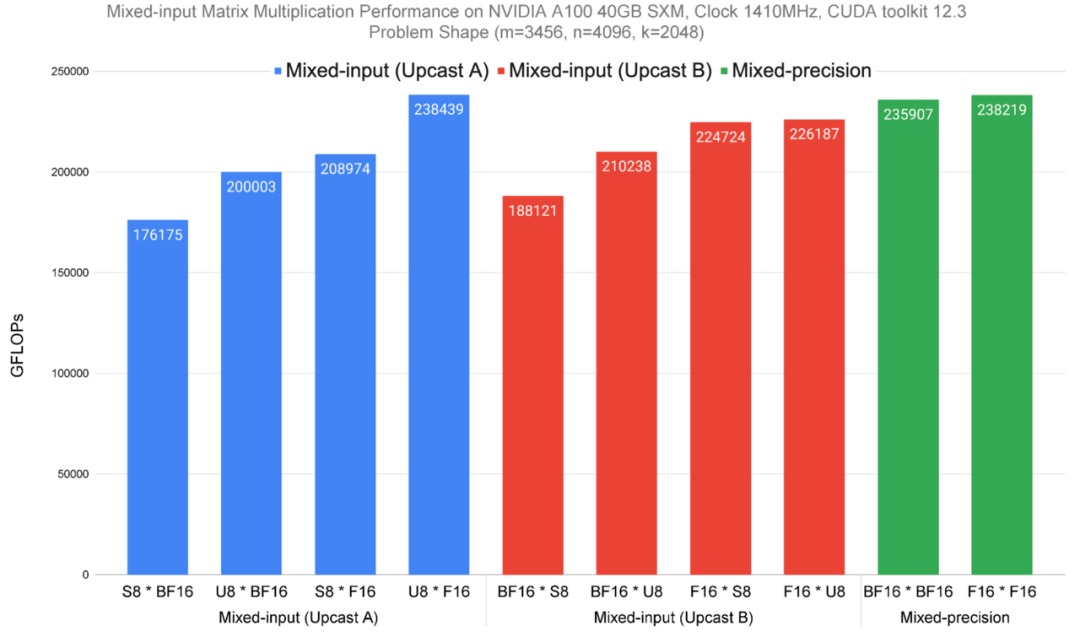
在NVIDIA A100 40GB SMX4芯片上,针对一个计算受限的矩阵问题,测试混合输入矩阵乘法的性能,其矩阵大小为m=3456,n=4096,k=2048。
致谢
在此,我们要特别感谢一些同仁,他们通过技术头脑风暴和博客文章改进做出了杰出贡献,包括Quentin Colombet,Jacques Pienaar,Allie Culp,Calin Cascaval,Ashish Gondimalla,Matt Walsh,Marek Kolodziej和Aman Bhatia。此外,我们还要对NVIDIA的合作伙伴Rawn Henry,Pradeep Ramani,Vijay Thakkar,Haicheng Wu,Andrew Kerr,Matthew Nicely和Vartika Singh表示由衷的感谢。

试用图片/视频生成加速引擎OneDiff: github.com/siliconflow/onediff



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


