
导语
涌现(Emergence)和因果(causality)是理解复杂系统的两个基本概念,它们之间相互关联。一方面,涌现指的是宏观性质不能仅归因于个体性质的现象。另一方面,因果性可以呈现出涌现,意味着随着抽象层次的提高,可能会出现新的因果定律。因果涌现理论旨在连接这两个概念,甚至使用因果性度量来量化涌现。近日,集智科学研究中心、北京师范大学与清华大学的研究者合作,在 Entropy「因果与复杂系统特刊」发表综述文章,全面回顾了因果涌现的定量理论和应用的最新进展。该综述解决了两个关键问题:量化因果涌现和在数据中识别涌现。解决后者需要使用机器学习技术,从而在因果涌现和人工智能之间建立联系。本文强调,用于识别因果涌现的架构与因果表征学习、因果模型抽象和基于世界模型的强化学习具有相通之处。
论文第一作者所属单位是集智科学研究中心,集智科学研究中心是门头沟民政局批准成立、门头沟科信局主管的民办非企业,致力于营造跨学科探索小生境,催化复杂性科学新理论。集智研究中心长期关注复杂科学中的核心问题,如涌现、因果、自指、意识、生命起源等等,并充分结合人工智能机器学习技术尝试解决这些问题。目前已有13篇文章发表于国际期刊,其中包括一篇因果涌现的综述和一篇生命起源的综述。这里的文章大部分产生于集智社区读书会。(访问集智科学研究中心网站了解详情:www.research.swarma.org/research)
研究领域:复杂系统,因果涌现,因果科学,部分信息分解 袁冰,吕奥博,王志鹏,杨明哲,刘凯威 | 作者张江 | 审校梁金 | 编辑
袁冰,吕奥博,王志鹏,杨明哲,刘凯威 | 作者张江 | 审校梁金 | 编辑

论文题目:
Emergence and Causality in Complex Systems: A Survey of Causal Emergence and Related Quantitative Studies
论文链接:https://www.mdpi.com/1099-4300/26/2/108论文作者:袁冰,张江,吕奥博,吴嘉赟,王志鹏,杨明哲,刘凯威,牟牧云,崔鹏
本文旨在对因果涌现的定量理论和应用的最新研究及相关工作进行全面综述。它还探讨了因果涌现、机器学习和复杂系统之间的联系。第2节中深入探讨了因果涌现的背景,特别关注复杂系统中因果和涌现之间的相互作用。第3节中介绍了各种定量理论框架,包括Crutchfield等人的计算力学、Seth等人的格兰杰因果涌现理论、Hoel等人的因果涌现理论和Rosas等人的部分信息分解涌现理论。此外,还讨论了粗粒度策略、有效信息度量和部分信息分解等相关概念,并对这些理论进行了比较分析。第4节讨论因果涌现理论和机器学习之间的联系。它探索使用机器学习和神经网络技术来识别因果涌现,并将有效信息的度量扩展到机器学习问题。最后,本文深入探讨了机器学习和复杂系统领域的其他重要主题和潜在应用。论文详细目录如下,希望深入研读论文的朋友可以参考原论文,以及扫描下方二维码查看作者们对论文的详细介绍:

https://pattern.swarma.org/article/292
论文目录
- 引言
- 背景:从因果到涌现
2.1 因果
2.2 涌现
- 用因果量化涌现
3.1. 早期相关工作3.2 计算力学3.3 G-Emergence 理论3.4 其他量化涌现的理论3.5 Erik Hoel 的因果涌现理论
3.6 Fernando Rosas 量化因果涌现的框架
- 因果涌现与机器学习
4.1 用机器学习识别因果涌现
4.2 为什么是“因果”涌现?
4.3 因果涌现用于机器学习
- 讨论与展望
5.1 因果涌现与因果表征学习
5.2 本体论和认识论的因果与涌现
5.3 复杂系统中的潜在应用
5.4 通过因果涌现理解复杂系统
1. 因果涌现理论进展概述
经济增长、环境保护、可持续发展、全球气候危机、社会不平等等诸多问题都与复杂的系统交织在一起[1][2],因此,深入了解复杂系统如何运行、演化、成长、稳定和崩溃至关重要。然而,由于复杂系统由通过复杂的非线性关系相互作用的不同且异构的主体组成[3],因此这项任务异常具有挑战性。此外,它们都表现出在复杂系统中非常常见却依然神秘的涌现现象[4]。
第一个活细胞如何从地球早期环境中各种分子之间的碰撞中涌现出来[5]?“我”的认知概念如何从我们大脑中无数神经元之间复杂的相互作用中产生[6]?大型神经语言模型如何突然展现出涌现能力[7]?这些基本问题围绕着复杂的生命、认知和人工系统中的涌现概念。涌现是指宏观属性和现象无法完全用单个组件属性加以解释的现象[4][8][9][10]。这对传统的还原论观点提出了巨大的挑战,同时也揭示了涌现现象神秘本质的根本原因。
然而,正如Bedau的弱涌现理论[10]所阐明的,许多涌现现象可以通过系统内个体之间的相互作用来理解[4]。事实上,复杂系统由交互作用组件构成的网络组成[11]。在这些网络中,即使是一个很小的原因,例如单个元素被扰动,也可以通过互连网络传播,从而产生集体效应。所描述的现象通常被称为蝴蝶效应[12],它为涌现发生提供了一种解释。另一方面,诸如内稳态(homeostasis)[13]之类的涌现特性可以稳定系统本身,从而将因果效应维持在局域层面而非宏观可观测层面。这些现象表明,复杂系统通过因果律实现相互作用,众多的局部因果律形成了相互关联的整体因果网络。而这个整体具有独特的因果特征。
因果关系是指原因与其结果之间的联系[14][15][16]。它描述了一种现象,其中一个事件(称为因)导致另一个事件(称为果)。传统的因果关系研究通常关注两个或几个变量之间的因果关系。然而,由于涉及大量变量和涌现现象的存在,复杂系统中因果关系的独特特征对经典因果科学提出了新的挑战。在复杂系统中,一个因可能会产生多个果,反之,一个果也可能会受到多个因的影响。此外,在复杂系统中,因果关系往往表现出跨层次的特性,这与涌现密切相关。
涌现和因果相互关联。一方面,涌现是复杂系统中各组成部分之间复杂和非线性相互作用的因果效应[8][9]。另一方面,涌现属性可能对复杂系统中的个体产生因果影响[4][17]。例如,化石燃料的价格是市场上买卖双方互动的结果。同时,价格也可能向市场提供反馈:它可以影响每个人的购买决策。
此外,我们还可以从因果关系的角度来理解涌现。涌现的意思是宏观层面上的一些现象和性质不能归因于微观性质[18]。因此,涌现的属性或现象失去了通常来自微观的直接解释,但却可以归因于宏观层面的原因,Erik Hoel在《因果涌现的定量计算表明宏观可以打败微观》[19]一文中分析了这一现象。也就是说,在更大尺度上可以观察到新的因果关系。
总之,深入理解涌现对复杂系统研究领域至关重要,涌现的定量理论的发展正方兴未艾。这样的理论有可能解决重大挑战,包括生命的起源[20]、大型神经网络模型中新奇能力的涌现,以及人工智能、意识和自由意志在人工系统中涌现的潜力[21]。因果关系不仅与涌现有着深刻的联系,许多研究人员还认为这是定量地理解涌现的最关键视角之一[18][19][22][23]。
从因果角度理解涌现有两个主要挑战:
-
第一个是建立涌现的定量定义;
- 第二个是通过数据分析识别涌现的行为或现象。
为了解决第一个挑战,过去十年出现了两种著名的涌现定量理论。第一个是Erik Hoel等人的因果涌现理论[19],第二个是Fernando E. Rosas等人的部分信息分解(PID)涌现理论[24]。
Hoel 等人的因果涌现理论专门针对使用马尔可夫链建模的复杂系统。它采用有效信息(EI)的概念来量化马尔可夫链内因果影响的程度,并针对同一系统在不同宏微观尺度下比较有效信息值[19][25]。因果涌现是通过宏观层面和微观层面的有效信息值差异来定义的:如果宏观有效信息值大于微观有效信息值,即发生因果涌现。Hoel还给出了几个离散马尔可夫链的证明例子。他和其他研究人员进一步扩展了具有连续变量[26]和复杂网络的动力系统[27]的有效信息和因果涌现的度量。尽管还有其他一些量化因果效应和因果涌现的方法,不过 Comolatti 和 Hoel 系统地比较了几种因果效应度量方法[28],得出结论是这些度量方法是相通的,都可以用几个通用的因果涌现度量定义来表达。
将系统的微观状态转换为宏观状态涉及到不同的粗粒化策略,显然粗粒化策略并不唯一。我们感兴趣的是能够引发因果涌现的粗粒化策略。然而,在Hoel的因果涌现理论中,给定粗粒化策略是计算宏观动力学的有效信息的前提。虽然通过最大化宏观有效信息,也能导出最优的粗粒化策略[19],然而由于计算复杂性,这项任务对于大规模系统来说非常挑战。为了解决这些问题,Rosas等人引入了一种新的不依赖于粗粒化方法的因果涌现的定量定义[24]。该定义借鉴了部分信息分解理论(PID),PID是Williams等人开发的一种方法,旨在将目标变量和源变量之间的互信息分解为不重叠的三种信息原子:特有信息、冗余信息和协同信息。在此基础上,Rosas进一步发展了这一概念,并引入了称为φlD的理论来分解多个目标变量和源变量之间的互信息。该框架基于系统的固有特征来定量刻画因果涌现,通过测量源变量和目标变量之间的协同信息,如果协同信息值大于零,即可判定发生了因果涌现。
第二个挑战是如何从观测数据中识别涌现。为了解决这个问题,Rosas等人推导了数值方法[24]。但Rosas的方法有些局限性,其一,这只是一种近似方法,且只能给出涌现的充分条件,其二,应用该方法时也需要预先定义粗粒度的宏状态变量。因此,仍然需要开发新的识别方法。
近年来,在机器学习和深度神经网络技术快速发展的推动下,人工智能取得了长足的进步。有两个关键方面需要在因果涌现的背景下考虑,首先,可以采用机器学习和神经网络技术来解决因果涌现识别的挑战。通过利用这些工具,我们可以开发有效检测和分析因果涌现现象的方法。其次,可以将因果涌现的概念和技术引入机器学习中,以增强模型的泛化能力。这种集成可以潜在地提高机器学习算法的泛化能力,使其远远超出训练数据,从而形成更强大、适应性更强的系统。
在张江等人最近的一项研究[31]中,引入了一种名为神经信息压缩机(NIS)的机器学习框架,以解决使用 Hoel 等人的框架在识别因果涌现时遇到的挑战。值得注意的是,NIS神经网络作为配备内部模型的“机器观察者”,表现出识别各种类型数据之间因果关系的非凡能力。这项工作的最新进展进一步开发了改进版的神经信息压缩机(NIS+),直接以最大化有效信息这一关键度量作为神经网络的训练目标[32]。通过对模拟数据和真实大脑数据进行的大量实验,NIS+ 证明了其自动发现新出现的宏观变量和宏观动力学的能力。因此,NIS+能够学到宏观动力学规律,并利用它来量化因果涌现。这些实验结果凸显了NIS+在捕获和分析因果涌现现象方面的有效性和潜力。
此外,NIS+通过直接最大化有效信息(EI),在泛化能力方面也展现出卓越的性能。这就引出了第二个问题:我们能否在因果涌现的背景下利用因果关系度量EI来增强神经网络对分布外(OOD)场景的泛化能力?这个概念被称为机器学习的因果涌现。通过探索这个想法,我们的目标是弥合因果涌现和机器学习之间的差距,开启提高机器学习泛化能力的新途径。
在下一节我们讨论几个重要的相关问题。首先,我们探讨了因果涌现和因果表征学习[33]这两个新兴领域之间的异同,揭示了这两个领域之间的相互关联。其次,我们深入研究了有关本体论或认识论意义上的因果和涌现的哲学问题,阐述了对其潜在哲学含义的见解。最后,我们讨论了因果涌现在复杂系统中的潜在应用,以及它如何有助于我们从因果涌现的角度理解复杂系统。这些讨论扩大了本文的范围,并为未来的研究提供了有趣的途径。
2. 未来展望
2.1 因果涌现与因果表征学习
因果表征学习是人工智能中一个新兴的领域[33],它结合了人工智能中的两个重要领域:表征学习和因果推理。表征学习旨在提取或表达隐藏在数据中的重要特征,以自动进行预测[139]。它可以视为深度学习的典型应用,并在图像分类[111]、人脸识别[112]、语言理解[113][114][115]、游戏AI操作[109][116]等领域取得了显著进展。然而,传统的表征学习有一个关键的局限性:它只能捕捉数据中的相关信息,而不能捕捉潜在的因果关系。因此,在表征学习中考虑因果关系是很重要的一环。
为了解决这个问题,因果表征学习试图结合表示学习和因果推理这两个子领域的优势,自动提取数据背后的重要特征和与因果关系[33]。
一个典型的因果表征学习场景如图所示。假设有一组变量和因果机制(包括因果图和结构方程)描述了机械臂和彩色方块的世界是如何运作的。然而,对于正在进行因果表征学习的主体来说,这些机制是不可直接观察到的。相反,主体可以观察到的是由机械臂和块生成的一组图像。因果学习框架的目标是从观察到的图像中提取因果变量和机制,这些变量和机制可以用于执行例如因果发现[140]、以及在不同环境[120]或区域[118][121]中做预测等其他下游任务。
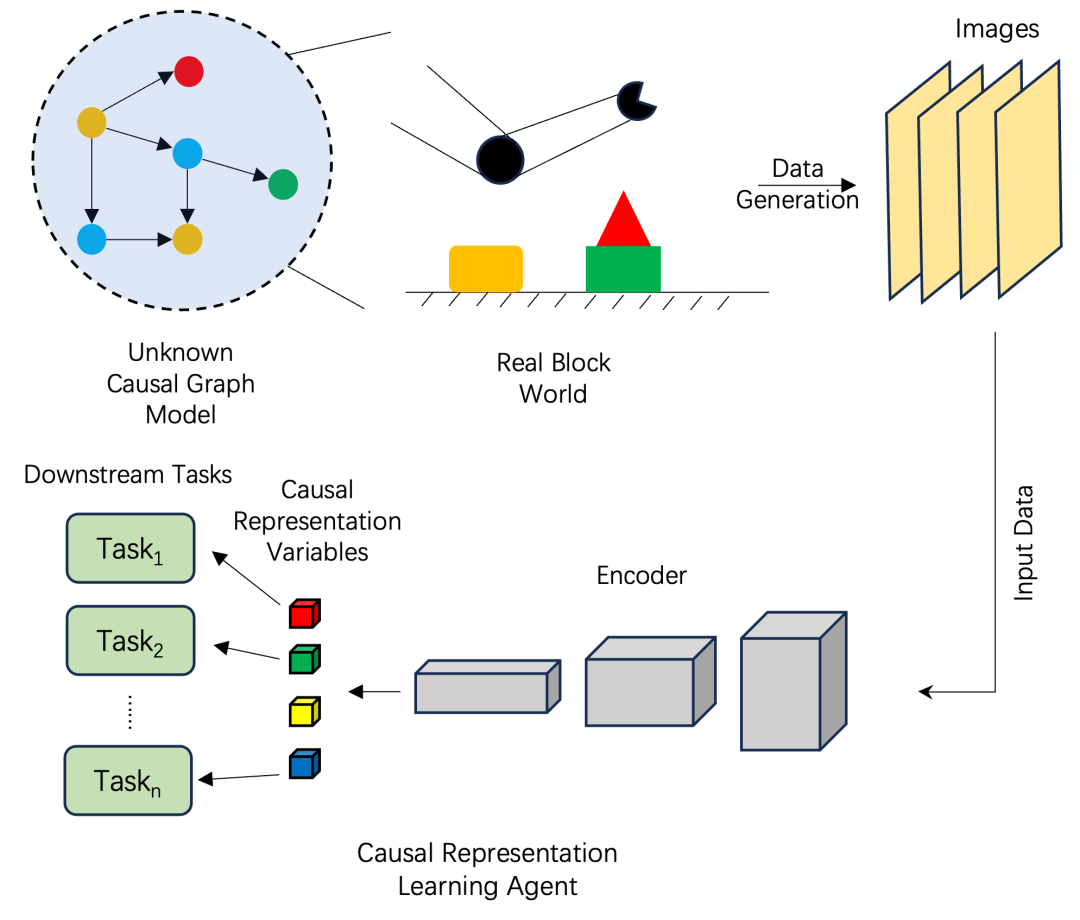
一个典型的因果表征学习(CRL)主体的工作流程说明。
这是一个典型的因果表征学习主体的工作流程说明。图的上部描绘了一个带有机械臂的真实区块世界和相应的因果图,表示真实世界中变量之间的关系,而这对主体者来说是完全未知的。此外,数据被呈现为由块世界生成的图像。图的下部描述了因果表征学习主体的结构。它利用卷积神经网络(CNN)从数据中提取有意义的表示,并基于这些表示执行向下的任务。编码器在从输入数据中捕捉相关特征和模式方面发挥着至关重要的作用,使主体能够学习和理解因果关系。
(1)相似之处
在Erik Hoel和因果表征学习的理论框架内比较因果涌现识别的任务是很有趣的。事实上,因果涌现识别的任务可以理解为因果表征学习的任务,其中宏观变量是因果变量,宏观动力学是因果机制,粗粒度策略是将原始数据转换为表征的编码过程。在这个框架内,EI可以被理解为因果效应对机制强度的衡量标准。为了识别因果涌现,我们需要学习适当的因果变量来表示数据,并在宏观层面(在表征潜在空间中)发现因果机制,以确保所学习的因果机制在潜在空间中的EI大于原始数据的EI。有了这些相似之处,这两个领域的技术和概念可以相互学习。例如,因果表征学习的技术可以应用于发现因果涌现。
另一方面,所学习的抽象因果表征可以被视为宏观状态,这增强了因果表征学习的可解释性。这一观点表明,因果表征学习本质上揭示了数据中隐藏的因果涌现特征。
此外,涌现现象和因果表征学习之间的这些相似之处有助于更深入地理解涌现本身。通过将因果表征学习框架应用于表现出涌现现象的动力系统生成的数据,我们可以提取更深刻的因果结构。这些深刻的因果结构可能是围绕涌现的奥秘的起源。通过深入研究因果表征学习的深度,揭示复杂系统中隐藏的因果关系,我们可以深入了解涌现现象背后的机制。这些因果结构可能为理解由简单成分的相互作用产生的新特性和行为的涌现提供基础。
(2)不同之处
然而,因果表征学习和因果涌现之间存在一些理论上的差异。最大的区别是因果表征学习假设数据背后有一个真正的因果机制,数据是由这个因果机制产生的[33]。相比之下,对于因果涌现识别,宏观层面的涌现变量和机制只是观察和理解数据的便捷方式,“真正的因果关系”可能并不存在。这些差异如下图所示。
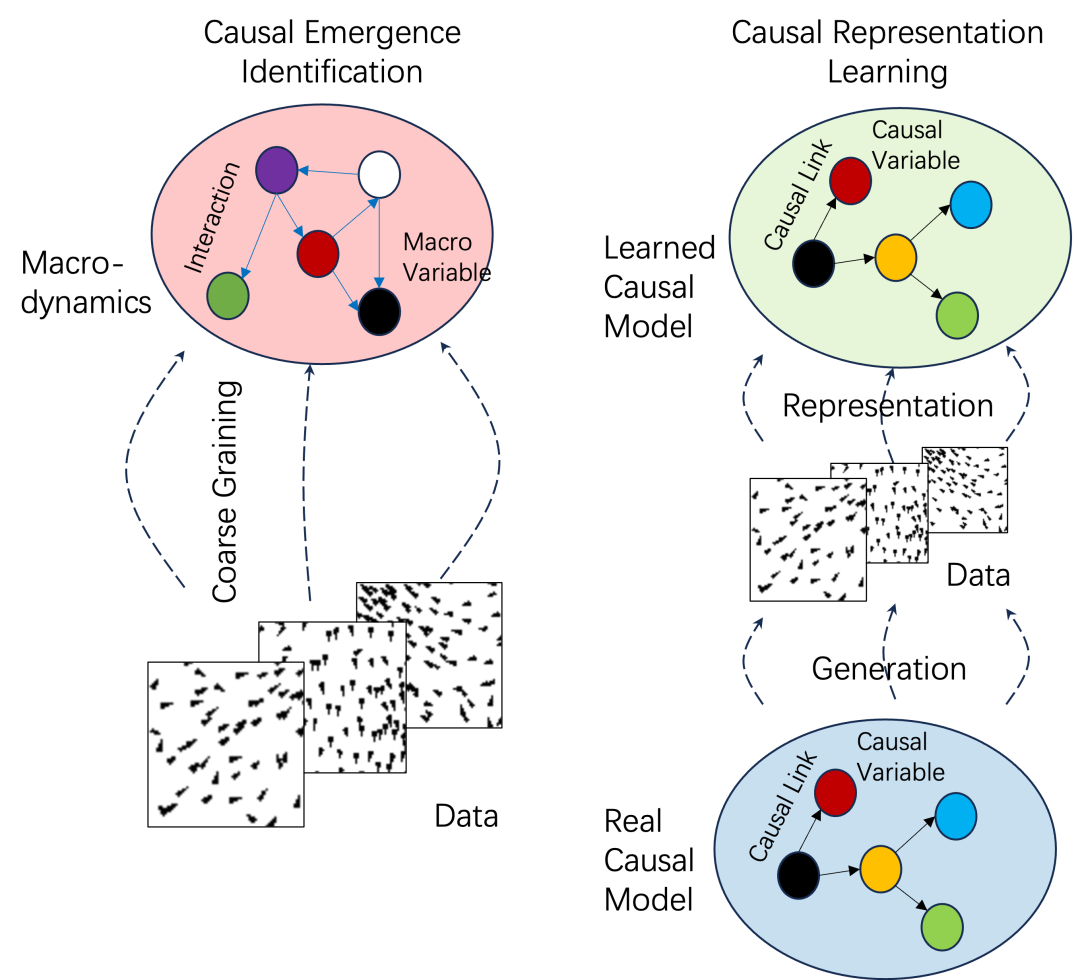 因果涌现识别与因果表征学习
因果涌现识别与因果表征学习
然而,如果采用认识论的观点,这种差异就会消失,因为这两种方法都从观测数据中提取有意义的信息,以获得具有更强因果效应的表示。
另一个主要区别是,宏观状态在因果涌现中的因果机制是一个动力系统。因此,如果在宏观状态空间中的是一个网络动力学,由于状态变量在动力系统中来回迭代可能会产生循环结构,因此这样的模型允许反馈和循环交互的存在。但在因果表征学习中采用结构因果模型来刻画因果机制,用图来表示就是一个不允许包含循环结构的有向无环图(DAG)。然而这些差异并不重要,因为马尔可夫动力学总是可以转换为因果模型。
最后一点区别,未知混淆变量在因果结构模型中扮演着非常重要的角色,然而在因果涌现中它们是被忽视的。
总之,因果涌现和因果表征学习之间有着深刻的联系。一方面,用于因果涌现识别的机器学习框架表现出与因果表征学习框架相似的结构。甚至这些概念也可以建立一一对应关系。因此,双方的思想和技术可以相互学习。另一方面,对因果涌现的研究可以为因果表征学习算法提供新的视角和见解。例如,我们可以将学习到的表征和因果机制解释为涌现的因果律。EI的最大化可以提高因果表征学习和强化学习主体学习因果关系的效率。
2.2 本体论和认识论的因果与涌现
尽管机器学习技术促进了因果结构和模型的学习,以及对涌现特性和因果关系的探索,但重要的是要考虑通过机器学习获得的结果是否反映了本体论因果关系和涌现,或者它们是否只是认识论现象。
在这里,本体论因果关系是指存在于客观现实中的因果关系,独立于我们的知识或理解。本体论因果关系探讨了在世界上产生因果效应的基本机制和相互作用。同样,本体论的涌现也与涌现属性的客观存在及其潜在机制有关。
另一方面,认识论因果关系侧重于我们对因果关系的认识和理解。它涉及我们如何根据观察和经验来感知、建模和解释因果关系,尽管现实中可能并不真实存在这样的因果关系。认识论的涌现,类似于认识论的因果关系,侧重于我们对涌现现象的理解和阐释。换言之,认识论因果关系和涌现取决于观察者,不同的观察者可能对特定客观对象的因果关系和涌现现象有不同的看法。
关于因果关系和涌现的本体论和认识论方面,历史上一直存在着长期的争论[17][22][68][76]。[68]的作者强调,文献中“因果关系”的概念往往是模糊的,应区分为“因(cause)”和“理由(reason)”,与本体论和认识论因果关系相一致,“因(cause)”是指充分造成影响的真正因素(因果闭合原理[141]和排除原理[142]),而“理由(reason)”只是个人理解影响的解释。理由可能不像真正的原因那样严谨,但它确实提供了一定程度的可预测性,在某些情况下会还是很有价值的。
然而,区分它们,特别是在处理具体现象时,仍然是一项具有挑战性的任务。其中一个有争议的概念是向下因果。向下因果关系是否客观存在的问题仍然悬而未决。在[24]中,Rosas认为向下因果不仅独立于特定的观察者存在,而且还能通过使用信息分解方法来提供向下因果的量化特征。然而,Yurchenko提出,区分因果(causality)和归因(reasoning)这两个独立的概念很重要。根据这一观点,向下的因果关系属于“理由(reason)”而非因果关系的范畴。在这种背景下,因果(causality)和归因(reasoning)可以分别被视为代表本体论和认识论的因果关系。(参看:《科学能解释自由意志吗?》)
同样,关于因果涌现性质的争论仍在继续。涌现的问题是,因果涌现是否是一种真正的现象,独立于特定的观察者而存在[77]。我们先前强调了不同的粗粒化策略可以导致不同的宏观动力机制,并具有不同的EI度量。本质上,不同的粗粒度策略可以被视为代表不同的观察者。然而,Hoel的理论提出了一个区分粗粒化方法的标准,即EI最大化。因此,对于给定的一组马尔可夫动力学,只有使EI测度最大化的粗粒度策略和相应的宏观动力学才能被视为客观结果。然而,当存在多个最大化EI的解决方案,引入一定程度的主观性时,就会出现挑战[77]。[31][32]的作者通过引入微观状态中预测误差的约束来解决这个问题,这部分缓解了这个问题。然而,最优结果是否具有唯一的解决方案仍然是一个悬而未决的问题,需要进一步研究。
同样,尽管机器学习的结合不能解决围绕本体论和认识论因果涌现的争论,但它提供了客观标准,有助于缓解主观性问题。这是因为机器学习算法努力优化目标函数。因此,机器学习主体可以被视为对因果涌现做出判断的“客观”观察者。这代表了结合机器学习的额外优势。然而,方案的唯一性问题在这种方法中至关重要,值得进一步关注。
机器学习的结果是本体论的还是认识论的?答案是认识论,它取决于机器学习算法。然而,这并不意味着机器学习的所有结果都是无意义的,因为如果学习主体经过良好的训练,并且定义的数学目标得到了有效的优化,那么结果也可以被认为是客观的,并且与算法无关。
对人类的认知提出同样的问题是很有趣的。人类大脑中的所有认知结果,包括因果关系、粗粒度策略和宏观动力学,都反映了客观现实吗?还是纯粹是认识论的?首先,回答这个问题极具挑战性。其次,特定人脑的认知结果必须客观地体现在神经网络结构中。因此,对于大脑来说,这些结果是本体论的。机器学习也有类似的原因。机器学习算法的认知结果通过神经网络中的结构和参数来记录。因此,研究这些结构可以揭示原始系统的性质,观察者和被观察对象之间相互作用的性质可以被机器客观地反映出来。
此外,建立一个集成了机器学习的理论框架,将有助于对观察者进行建模,也有助于研究观察者与被观测复杂系统之间的相互作用。这个框架不仅使我们能够探索有关因果涌现的难题,而且还能够理解观察者的边界和局限性。这项研究的一个例子是利用机器学习算法形成信息瓶颈,从而让量子系统涌现出了经典特性[143]。
2.3 复杂系统中的潜在应用
在本小节中,我们将讨论因果涌现识别、机器学习和因果推理相关的技术在复杂系统中的潜在应用。复杂系统可以被理解为一个大型网络,事件通过因果关系联系在一起。从数据中自动发现复杂的因果关系是一个具有挑战性的问题。因果发现试图通过各种方式来解决这个问题[144][145][146][147][148][149]。然而,当在复杂系统中应用这些因果发现方法时,可能会出现额外的挑战,因为可能存在循环因果结构和跨层级因果关系。
由于反馈效应,循环因果结构广泛存在于复杂动力系统中。也就是说,一个变量可能通过直接的自循环反馈或形成环形长链影响自己。这种循环因果结构可能会对现有的因果方法提出挑战,因为这些方法大多研究有向无环因果图。然而,最近的进展已经见证了一些以数据驱动的方式发现这些循环结构方法的发展,例如[46][47][48][49][150][151][152][153]。
另一个方面是,如果考虑到尺度和粗粒化的成分,可能存在更高层次或跨层次的因果关系。例如,向下因果关系描述了宏观层面和微观层面变量之间的因果效应。因此,因果关系可能是跨层次的。如果因果涌现出现在一个复杂系统中,那么在宏观变量之间可能会发现一些显著的因果关系。复杂系统中的所有这些因素都提出了新的挑战。机器学习方法可以解决宏观层面是否存在更高层次因果关系的问题。然而需要注意的是,用这样的方法所能找到的是一个全局性的因果度量。它必须进一步发展和扩展,以找到宏观变量或宏观变量与微观变量之间的局部因果关系[98]。此外,现有的因果发现方法有必要扩展到考虑对一组变量进行分组或对系统进行粗粒化处理的方法。例如,[154]提出了一种基于格兰杰因果和图神经网络的从粗到细因果发现算法,可以按从粗到精的顺序对变量进行分组,从而提高算法的效率。其他多层次因果发现方法也在[155][156][157]中提出和讨论。
另一个有趣的问题是涌现探测。在复杂动力系统中,各种更高层次的模式,如波、周期振荡和孤子,无处不在。例如,在气候系统中,台风和龙卷风是涌现的涡旋结构。在城市地区,交通堵塞也是大量汽车相互作用的结果。社会骚乱是人类社会更高层涌现事件的又一个例子。在早期识别这些涌现模式至关重要[81,158,159,160,161,162]。因此,迫切需要一种方法能够自动检测这些涌现模式甚至提供预警信号。
在这篇综述中,我们主要关注因果关系的涌现;然而,我们并不局限于这种特定类型的涌现。更宏观或全局层面的属性也可能是涌现的,尽管因果涌现可能是最重要的一个。例如,在[163]中,作者讨论了涌现信息封闭的概念,它指的是主体内编码的信息可以形成一个不受外部世界影响的封闭系统。然后,作者认为这种具有信息封闭性的主体可以被视为一种意识。对称性可能是一些复杂系统中另一个有趣的性质,它可能是涌现的。例如,在二维欧几里得空间中,大量随机游走者的任何单个轨迹都是随机的。然而,描述每个小区域中跌倒的随机游走者数量如何随不同位置而变化的高斯分布面是各向同性的。这种对称性只能在宏观层面上找到,因此,它也是涌现的。部署一种自动发现这种涌现对称性的方法将会是有趣并且有用的。
然而,至关重要的是要认识到将机器学习技术应用于因果发现和涌现识别问题的固有局限性。例如,在[45]中,作者强调了存在“统计上等效”但因果上不同的DAG族,这意味着可以构建不同的因果结构来解释同一组数据集。当利用机器学习技术来揭示因果关系和涌现特性时,就需要解决类似的挑战。这方面的进一步研究值得高度重视。
2.4 通过因果涌现理解复杂系统
对因果涌现和涌现的因果的深刻理解可以为理解复杂系统中的各种神秘现象提供见解,包括生命系统、社会系统、气候系统、生态系统等。值得注意的是,如自由意志[68]、意识[165]和生命等基本问题,都与涌现的因果密切相关[166]。例如,自由意志可以被视为向下因果的一种涌现形式[167]。社会现象可以通过因果涌现的视角来理解。有趣的是,因果涌现的EI和ϕID框架都与一种意识理论——整合信息论(IIT)有联系[168]。然而,在因果涌现的的背景下理解这些抽象的概念和现象仅仅是第一步。
对于一个特定系统,有三个问题需要在未来的研究中解决:(1)因果涌现何时出现?(2) 涌现的因果如何对系统功能产生影响?(3) 当系统被改变以适应环境时,涌现的因果是如何变化的?我们逐一讨论这些问题。
我们仍然不知道因果涌现何时会发生,以及因果涌现的衡量标准如何随着系统的一些关键参数而变化。在[32]中,作者展示了鸟群(Boid)模型中因果涌现的测度如何随着不同噪声的变化而变化。当一些关键参数发生变化时,可以合理地预期在复杂系统中存在关于涌现的因果的相变,因为因果关系或因果效应的强度也是一个全局性质,并且可能取决于一些序参量。
如果系统中发生了因果涌现,那么涌现的因果如何影响系统的各个部分和整体?例如,“自我”可以被理解为一个涌现的宏观变量[68],“自我”是如何影响身体其他部分的,比如脚的运动?这个问题并不无聊,因为它涉及到身心互动的问题。重要的是,要理解这一现象,必须同时从宏观和微观两个层面研究信息流。
最后,适应和涌现之间的关系是什么[4][169][170]?有时,当我们将一个属性称为涌现属性时,本质上是指这个属性可以通过适应来发展。因此,适应或演化是某些涌现特性的因果力。这一概念也适用于涌现的因果。例如,在复杂系统中常见的向下因果就是适应和演化的结果。下一个关键问题是,如何才能让一种涌现性质或因果关系通过演化而发生?这个问题好像是要设计涌现[171][172][173]。然而,与其说我们的目的是寻求一种设计,不如说是想寻求一种解释。我们想了解的是哪些被我们看到的涌现的因果是通过什么样的具体环境和方式而演化出来的。
所有这些问题都需要在未来进一步研究。然而,这些还只是冰山一角,更多更有趣的问题还在等着我们去关注和研究。
参考文献
- Ledford, H. How to solve the world’s biggest problems. Nature 2015, 525, 308–311. [Google Scholar] [CrossRef] [PubMed]
- Mensah, P.; Katerere, D.; Hachigonta, S.; Roodt, A. Systems Analysis Approach for Complex Global Challenges; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Bar-Yam, Y. General features of complex systems. In Encyclopedia of Life Support Systems (EOLSS); UNESCO, EOLSS Publishers: Oxford, UK, 2002; Volume 1. [Google Scholar]
- Holland, J.H. Emergence: From Chaos to Order; OUP: Oxford, UK, 2000. [Google Scholar]
- Artime, O.; De Domenico, M. From the origin of life to pandemics: Emergent phenomena in complex systems. Philos. Trans. R. Soc. A 2022, 380, 20200410. [Google Scholar] [CrossRef] [PubMed]
- Lagercrantz, H.; Changeux, J.P. The emergence of human consciousness: From fetal to neonatal life. Pediatr. Res.2009, 65, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Tay, Y.; Bommasani, R.; Raffel, C.; Zoph, B.; Borgeaud, S.; Yogatama, D.; Bosma, M.; Zhou, D.; Metzler, D.; et al. Emergent abilities of large language models. arXiv 2022, arXiv:2206.07682. [Google Scholar]
- Anderson, P.W. More is different: Broken symmetry and the nature of the hierarchical structure of science. Science1972, 177, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Meehl, P.E.; Sellars, W. The concept of emergence. Minn. Stud. Philos. Sci. 1956, 1, 239–252. [Google Scholar]
- Bedau, M.A. Weak emergence. Philos. Perspect. 1997, 11, 375–399. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Wikipedia. Butterfly Effect—Wikipedia, The Free Encyclopedia. 2023. Available online: https://en.wikipedia.org/wiki/Butterfly_effect (accessed on 27 September 2023).
- Wikipedia. Homeostasis—Wikipedia, The Free Encyclopedia. 2023. Available online: https://en.wikipedia.org/wiki/Homeostasis (accessed on 4 October 2023).
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Pearl, J. Models, Reasoning and Inference; Cambridge University Press: Cambridge, UK, 2000; Volume 19. [Google Scholar]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kim, J. ‘Downward causation’ in emergentism and nonreductive physicalism. In Emergence or Reduction; Walter de Gruyter: Berlin, Germany, 1992; pp. 119–138. [Google Scholar]
- Fromm, J. Types and forms of emergence. arXiv 2005, arXiv:nlin/0506028. [Google Scholar]
- Hoel, E.P.; Albantakis, L.; Tononi, G. Quantifying causal emergence shows that macro can beat micro. Proc. Natl. Acad. Sci. USA 2013, 110, 19790–19795. [Google Scholar] [CrossRef] [PubMed]
- Ellis, G.F. Efficient, formal, material, and final causes in biology and technology. Entropy 2023, 25, 1301. [Google Scholar] [CrossRef] [PubMed]
- Oizumi, M.; Albantakis, L.; Tononi, G. From the phenomenology to the mechanisms of consciousness: Integrated information theory 3.0. PLoS Comput. Biol. 2014, 10, e1003588. [Google Scholar] [CrossRef] [PubMed]
- Crutchfield, J.P.; Young, K. Inferring statistical complexity. Phys. Rev. Lett. 1989, 63, 105. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.K. Measuring emergence via nonlinear Granger causality. alife 2008, 2008, 545–552. [Google Scholar]
- Rosas, F.E.; Mediano, P.A.; Jensen, H.J.; Seth, A.K.; Barrett, A.B.; Carhart-Harris, R.L.; Bor, D. Reconciling emergences: An information-theoretic approach to identify causal emergence in multivariate data. PLoS Comput. Biol. 2020, 16, e1008289. [Google Scholar] [CrossRef]
- Hoel, E.P. When the Map Is Better Than the Territory. Entropy 2017, 19, 188. [Google Scholar] [CrossRef]
- Chvykov, P.; Hoel, E. Causal geometry. Entropy 2020, 23, 24. [Google Scholar] [CrossRef]
- Klein, B.; Hoel, E. The emergence of informative higher scales in complex networks. Complexity 2020, 2020, 8932526. [Google Scholar] [CrossRef]
- Comolatti, R.; Hoel, E. Causal emergence is widespread across measures of causation. arXiv 2022, arXiv:2202.01854. [Google Scholar]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv 2010, arXiv:1004.2515. [Google Scholar]
- Mediano, P.A.; Rosas, F.; Carhart-Harris, R.L.; Seth, A.K.; Barrett, A.B. Beyond integrated information: A taxonomy of information dynamics phenomena. arXiv 2019, arXiv:1909.02297. [Google Scholar]
- Zhang, J.; Liu, K. Neural information squeezer for causal emergence. Entropy 2022, 25, 26. [Google Scholar] [CrossRef]
- Yang, M.; Wang, Z.; Liu, K.; Rong, Y.; Yuan, B.; Zhang, J. Finding emergence in data: Causal emergence inspired dynamics learning. arXiv 2023, arXiv:2308.09952. [Google Scholar]
- Schölkopf, B.; Locatello, F.; Bauer, S.; Ke, N.R.; Kalchbrenner, N.; Goyal, A.; Bengio, Y. Toward causal representation learning. Proc. IEEE 2021, 109, 612–634. [Google Scholar] [CrossRef]
- Iwasaki, Y.; Simon, H.A. Causality and model abstraction. Artif. Intell. 1994, 67, 143–194. [Google Scholar] [CrossRef]
- Sucar, L.E. Probabilistic Graphical Models; Advances in Computer Vision and Pattern Recognition; Springer: London, UK, 2015; Volume 10, p. 1. [Google Scholar]
- Rubin, D.B. Causal inference using potential outcomes: Design, modeling, decisions. J. Am. Stat. Assoc. 2005, 100, 322–331. [Google Scholar] [CrossRef]
- Malinsky, D.; Danks, D. Causal discovery algorithms: A practical guide. Philos. Compass 2018, 13, e12470. [Google Scholar] [CrossRef]
- Spirtes, P.; Glymour, C.; Scheines, R. Causation Prediction and Search, 2nd ed.; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Chickering, D.M. Learning equivalence classes of Bayesian-network structures. J. Mach. Learn. Res. 2002, 2, 445–498. [Google Scholar]
- Hume, D. An enquiry concerning human understanding. In Seven Masterpieces of Philosophy; Routledge: Abingdon, UK, 2016; pp. 183–276. [Google Scholar]
- Eells, E. Probabilistic Causality; Cambridge University Press: Cambridge, UK, 1991; Volume 1. [Google Scholar]
- Suppes, P. A probabilistic theory of causality. Br. J. Philos. Sci. 1973, 24, 409–410. [Google Scholar]
- Hoel, E.; Levin, M. Emergence of informative higher scales in biological systems: A computational toolkit for optimal prediction and control. Commun. Integr. Biol. 2020, 13, 108–118. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Textor, J.; Van der Zander, B.; Gilthorpe, M.S.; Liśkiewicz, M.; Ellison, G.T. Robust causal inference using directed acyclic graphs: The R package ‘dagitty’. Int. J. Epidemiol. 2016, 45, 1887–1894. [Google Scholar] [CrossRef] [PubMed]
- Richardson, T.S. A discovery algorithm for directed cyclic graphs. arXiv 2013, arXiv:1302.3599. [Google Scholar]
- Spirtes, P.L. Directed cyclic graphical representations of feedback models. arXiv 2013, arXiv:1302.4982. [Google Scholar]
- Lacerda, G.; Spirtes, P.L.; Ramsey, J.; Hoyer, P.O. Discovering cyclic causal models by independent components analysis. arXiv 2012, arXiv:1206.3273. [Google Scholar]
- Forré, P.; Mooij, J.M. Constraint-based causal discovery for non-linear structural causal models with cycles and latent confounders. arXiv 2018, arXiv:1807.03024. [Google Scholar]
- Ellison, G.T. Using Directed Acyclic Graphs (Dags) to Represent the Data Generating Mechanisms of Disease and Healthcare Pathways: A Guide for Educators, Students, Practitioners and Researchers. In Teaching Biostatistics in Medicine and Allied Health Sciences; Springer: Berlin/Heidelberg, Germany, 2023; pp. 61–101. [Google Scholar]
- Gong, C.; Yao, D.; Zhang, C.; Li, W.; Bi, J. Causal Discovery from Temporal Data: An Overview and New Perspectives. arXiv 2023, arXiv:2303.10112. [Google Scholar]
- Pepper, S.C. Emergence. J. Philos. 1926, 23, 241–245. [Google Scholar] [CrossRef]
- Winning, J.; Bechtel, W. Complexity, control and goal-directedness in biological systems. In The Routledge Handbook of Emergence; Routledge: Abingdon, UK, 2019; p. 134. [Google Scholar]
- Hendry, R.F. Substance and structure. In The Routledge Handbook of Emergence; Routledge: Abingdon, UK, 2019; p. 339. [Google Scholar]
- Huxley, T.H. Evolution and Ethics 1893–1943; Pilot Press: King’s Lynn, UK, 1947. [Google Scholar]
- Mill, J.S. Of the Composition of Causes. In A System of Logic, Ratiocinative and Inductive: Being a Connected View of the Principles of Evidence, and the Methods of Scientific Investigation; Cambridge Library Collection—Philosophy; Cambridge University Press: Cambridge, UK, 2011; Volume 1, pp. 425–436. [Google Scholar] [CrossRef]
- Gibb, S.; Hendry, R.F.; Lancaster, T. The Routledge Handbook of Emergence; Routledge: Abingdon, UK, 2019. [Google Scholar]
- Ross, W.D.; Smith, J.A. The Works of Aristotle: Metaphysica, by WD Ross; Clarendon Press: Cambridge, UK, 1908; Volume 8. [Google Scholar]
- Holland, J.H. Hidden Order: How Adaptation Builds Complexity; Addison Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1996. [Google Scholar]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 27–31 July 1987; pp. 25–34. [Google Scholar]
- Gardner, M. The Fantastic Combinations of Jhon Conway’s New Solitaire Game’Life. Sc. Am. 1970, 223, 20–123. [Google Scholar]
- Luhmann, N. Social Systems; Stanford University Press: Redwood City, CA, USA, 1995. [Google Scholar]
- Crutchfield, J.P. The calculi of emergence: Computation, dynamics and induction. Phys. D Nonlinear Phenom. 1994, 75, 11–54. [Google Scholar] [CrossRef]
- Bedau, M.A.; Humphreys, P. Emergence: Contemporary Readings in Philosophy and Science; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Bedau, M. Downward causation and the autonomy of weak emergence. Principia Int. J. Epistemol. 2002, 6, 5–50. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media Champaign: Champaign, IL, USA, 2002; Volume 5. [Google Scholar]
- Merton, R.K. The Sociology of Science: Theoretical and Empirical Investigations; University of Chicago Press: Chicago, IL, USA, 1973. [Google Scholar]
- Yurchenko, S.B. Can there be a synergistic core emerging in the brain hierarchy to control neural activity by downward causation? TechRxiv 2023. [Google Scholar] [CrossRef]
- Harré, R. The Philosophies of Science; Oxford University Press: New York, NY, USA, 1985. [Google Scholar]
- Baas, N.A. Emergence, hierarchies, and hyperstructures. In Artificial Life III, SFI Studies in the Science of Complexity, XVII; Routledge: Abingdon, UK, 1994; pp. 515–537. [Google Scholar]
- Newman, D.V. Emergence and strange attractors. Philos. Sci. 1996, 63, 245–261. [Google Scholar] [CrossRef]
- O’Connor, T. Emergent properties. Am. Philos. Q. 1994, 31, 91–104. [Google Scholar]
- Héder, M.; Paksi, D. A Criticism of Weak Emergence. Polanyiana 2019, 28, 1–2. [Google Scholar]
- Jackson, F.; Pettit, P. In defense of explanatory ecumenism. Econ. Philos. 1992, 8, 1–21. [Google Scholar] [CrossRef]
- Kim, J. Making sense of emergence. Philos. Stud. Int. J. Philos. Anal. Tradit. 1999, 95, 3–36. [Google Scholar]
- Bonabeau, E.; Dessalles, J.L. Detection and emergence. arXiv 2011, arXiv:1108.4279. [Google Scholar] [CrossRef]
- Dewhurst, J. Causal emergence from effective information: Neither causal nor emergent? Thought J. Philos. 2021, 10, 158–168. [Google Scholar] [CrossRef]
- Eberhardt, F.; Lee, L.L. Causal emergence: When distortions in a map obscure the territory. Philosophies 2022, 7, 30. [Google Scholar] [CrossRef]
- Shalizi, C.R. Causal Architecture, Complexity and Self-Organization in Time Series and Cellular Automata; The University of Wisconsin-Madison: Madison, WI, USA, 2001. [Google Scholar]
- Shalizi, C.R.; Moore, C. What is a macrostate? Subjective observations and objective dynamics. arXiv 2003, arXiv:condmat/0303625. [Google Scholar]
- Mnif, M.; Müller-Schloer, C. Quantitative emergence. In Organic Computing—A Paradigm Shift for Complex Systems; Springer: Basel, Switzerland, 2011; pp. 39–52. [Google Scholar]
- Tang, M.; Mao, X. Information entropy-based metrics for measuring emergences in artificial societies. Entropy 2014, 16, 4583–4602. [Google Scholar] [CrossRef]
- Fisch, D.; Jänicke, M.; Sick, B.; Müller-Schloer, C. Quantitative emergence–A refined approach based on divergence measures. In Proceedings of the 2010 Fourth IEEE International Conference on Self-Adaptive and Self-Organizing Systems, Budapest, Hungary, 27 September–1 October 2010; IEEE Computer Society: Washington, DC, USA, 2010; pp. 94–103. [Google Scholar]
- Fisch, D.; Fisch, D.; Jänicke, M.; Kalkowski, E.; Sick, B. Techniques for knowledge acquisition in dynamically changing environments. ACM Trans. Auton. Adapt. Syst. (TAAS) 2012, 7, 1–25. [Google Scholar] [CrossRef]
- Fisch, D.; Jänicke, M.; Müller-Schloer, C.; Sick, B. Divergence measures as a generalised approach to quantitative emergence. In Organic Computing—A Paradigm Shift for Complex Systems; Springer: Basel, Switzerland, 2011; pp. 53–66. [Google Scholar]
- Holzer, R.; De Meer, H.; Bettstetter, C. On autonomy and emergence in self-organizing systems. In International Workshop on Self-Organizing Systems, Proceedings of the Third International Workshop, IWSOS 2008, Vienna, Austria, 10–12 December 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 157–169. [Google Scholar]
- Holzer, R.; de Meer, H. Methods for approximations of quantitative measures in self-organizing systems. In Proceedings of the Self-Organizing Systems: 5th International Workshop, IWSOS 2011, Karlsruhe, Germany, 23–24 February 2011; Proceedings 5. Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–15. [Google Scholar]
- Teo, Y.M.; Luong, B.L.; Szabo, C. Formalization of emergence in multi-agent systems. In Proceedings of the 1st ACM SIGSIM Conference on Principles of Advanced Discrete Simulation, Montreal, QC, Canada, 19–22 May 2013; pp. 231–240. [Google Scholar]
- Szabo, C.; Teo, Y.M. Formalization of weak emergence in multiagent systems. ACM Trans. Model. Comput. Simul. (TOMACS) 2015, 26, 1–25. [Google Scholar] [CrossRef]
- Christensen, K.; Moloney, N.R. Complexity and Criticality; World Scientific Publishing Company: Singapore, 2005; Volume 1. [Google Scholar]
- McComb, W.D. Renormalization Methods: A Guide for Beginners; OUP Oxford: Cambridge, UK, 2003. [Google Scholar]
- Kemeny, J.; Snell, J. Finite Markov Chains: With a New Appendix “Generalization of a Fundamental Matrix”; Undergraduate Texts in Mathematics; Springer: New York, NY, USA, 1983. [Google Scholar]
- Pfante, O.; Bertschinger, N.; Olbrich, E.; Ay, N.; Jost, J. Comparison between different methods of level identification. Adv. Complex Syst. 2014, 17, 1450007. [Google Scholar] [CrossRef]
- Kotsalis, G.; Megretski, A.; Dahleh, M.A. Balanced truncation for a class of stochastic jump linear systems and model reduction for hidden Markov models. IEEE Trans. Autom. Control 2008, 53, 2543–2557. [Google Scholar] [CrossRef]
- White, L.B.; Mahony, R.; Brushe, G.D. Lumpable hidden Markov models-model reduction and reduced complexity filtering. IEEE Trans. Autom. Control 2000, 45, 2297–2306. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Grochow, J.A.; Libby, E.; DeDeo, S. Optimal high-level descriptions of dynamical systems. arXiv2014, arXiv:1409.7403. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620. [Google Scholar] [CrossRef]
- Varley, T.F. Flickering emergences: The question of locality in information-theoretic approaches to emergence. Entropy 2022, 25, 54. [Google Scholar] [CrossRef]
- Cheng, P.W.; Novick, L.R. Causes versus enabling conditions. Cognition 1991, 40, 83–120. [Google Scholar] [CrossRef] [PubMed]
- Varley, T.F. Causal emergence in discrete and continuous dynamical systems. arXiv 2020, arXiv:2003.13075. [Google Scholar]
- Marrow, S.; Michaud, E.J.; Hoel, E. Examining the Causal Structures of Deep Neural Networks Using Information Theory. Entropy 2020, 22, 1429. [Google Scholar] [CrossRef] [PubMed]
- Griebenow, R.; Klein, B.; Hoel, E. Finding the right scale of a network: Efficient identification of causal emergence through spectral clustering. arXiv 2019, arXiv:1908.07565. [Google Scholar]
- Klein, B.; Swain, A.; Byrum, T.; Scarpino, S.V.; Fagan, W.F. Exploring noise, degeneracy and determinism in biological networks with the einet package. Methods Ecol. Evol. 2022, 13, 799–804. [Google Scholar] [CrossRef]
- Klein, B.; Hoel, E.; Swain, A.; Griebenow, R.; Levin, M. Evolution and emergence: Higher order information structure in protein interactomes across the tree of life. Integr. Biol. 2021, 13, 283–294. [Google Scholar] [CrossRef] [PubMed]
- Swain, A.; Williams, S.D.; Di Felice, L.J.; Hobson, E.A. Interactions and information: Exploring task allocation in ant colonies using network analysis. Anim. Behav. 2022, 189, 69–81. [Google Scholar] [CrossRef]
- Luppi, A.I.; Mediano, P.A.; Rosas, F.E.; Holland, N.; Fryer, T.D.; O’Brien, J.T.; Rowe, J.B.; Menon, D.K.; Bor, D.; Stamatakis, E.A. A synergistic core for human brain evolution and cognition. Nat. Neurosci. 2022, 25, 771–782. [Google Scholar] [CrossRef]
- Varley, T.F.; Hoel, E. Emergence as the conversion of information: A unifying theory. Philos. Trans. R. Soc. A 2022, 380, 20210150. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Dabney, W.; Kurth-Nelson, Z.; Uchida, N.; Starkweather, C.K.; Hassabis, D.; Munos, R.; Botvinick, M. A distributional code for value in dopamine-based reinforcement learning. Nature 2020, 577, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.; Bridgland, A.; et al. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wang, Y.; Zhou, Z.; Ji, X.; Gong, D.; Zhou, J.; Li, Z.; Liu, W. Cosface: Large margin cosine loss for deep face recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5265–5274. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Fan, L.; Li, L.; Ma, Z.; Lee, S.; Yu, H.; Hemphill, L. A bibliometric review of large language models research from 2017 to 2023. arXiv 2023, arXiv:2304.02020. [Google Scholar]
- Cui, P.; Athey, S. Stable learning establishes some common ground between causal inference and machine learning. Nat. Mach. Intell. 2022, 4, 110–115. [Google Scholar] [CrossRef]
- Kaddour, J.; Lynch, A.; Liu, Q.; Kusner, M.J.; Silva, R. Causal machine learning: A survey and open problems. arXiv2022, arXiv:2206.15475. [Google Scholar]
- Peters, J.; Bühlmann, P.; Meinshausen, N. Causal inference by using invariant prediction: Identification and confidence intervals. J. R. Stat. Soc. Ser. B Stat. Methodol. 2016, 78, 947–1012. [Google Scholar] [CrossRef]
- Kuang, K.; Cui, P.; Athey, S.; Xiong, R.; Li, B. Stable prediction across unknown environments. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1617–1626. [Google Scholar]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Teshima, T.; Ishikawa, I.; Tojo, K.; Oono, K.; Ikeda, M.; Sugiyama, M. Coupling-based invertible neural networks are universal diffeomorphism approximators. Adv. Neural Inf. Process. Syst. 2020, 33, 3362–3373. [Google Scholar]
- Rosenblatt, M. Remarks on some nonparametric estimates of a density function. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Snoek, L.; van der Miesen, M.M.; Beemsterboer, T.; Van Der Leij, A.; Eigenhuis, A.; Steven Scholte, H. The Amsterdam Open MRI Collection, a set of multimodal MRI datasets for individual difference analyses. Sci. Data2021, 8, 85. [Google Scholar] [CrossRef] [PubMed]
- Arjovsky, M.; Bottou, L.; Gulrajani, I.; Lopez-Paz, D. Invariant risk minimization. arXiv 2019, arXiv:1907.02893. [Google Scholar]
- Ye, H.; Xie, C.; Cai, T.; Li, R.; Li, Z.; Wang, L. Towards a theoretical framework of out-of-distribution generalization. Adv. Neural Inf. Process. Syst. 2021, 34, 23519–23531. [Google Scholar]
- Huh, D.; Baidya, A. The Missing Invariance Principle found–the Reciprocal Twin of Invariant Risk Minimization. Adv. Neural Inf. Process. Syst. 2022, 35, 23023–23035. [Google Scholar]
- Zhao, H.; Des Combes, R.T.; Zhang, K.; Gordon, G. On learning invariant representations for domain adaptation. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 7523–7532. [Google Scholar]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 2016, 17, 1–35. [Google Scholar]
- Wang, J.; Lan, C.; Liu, C.; Ouyang, Y.; Qin, T.; Lu, W.; Chen, Y.; Zeng, W.; Yu, P. Generalizing to unseen domains: A survey on domain generalization. IEEE Trans. Knowl. Data Eng. 2022, 35, 8052–8072. [Google Scholar] [CrossRef]
- Li, Y.; Gong, M.; Tian, X.; Liu, T.; Tao, D. Domain generalization via conditional invariant representations. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Koyama, M.; Yamaguchi, S. Out-of-distribution generalization with maximal invariant predictor. arXiv 2020, arXiv:2008.01883. [Google Scholar]
- Ahuja, K.; Caballero, E.; Zhang, D.; Gagnon-Audet, J.C.; Bengio, Y.; Mitliagkas, I.; Rish, I. Invariance principle meets information bottleneck for out-of-distribution generalization. Adv. Neural Inf. Process. Syst. 2021, 34, 3438–3450. [Google Scholar]
- Kaur, J.N.; Kiciman, E.; Sharma, A. Modeling the data-generating process is necessary for out-of-distribution generalization. arXiv 2022, arXiv:2206.07837. [Google Scholar]
- Shen, Z.; Cui, P.; Zhang, T.; Kunag, K. Stable learning via sample reweighting. In Proceedings of the Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5692–5699. [Google Scholar]
- Shen, Z.; Cui, P.; Liu, J.; Zhang, T.; Li, B.; Chen, Z. Stable learning via differentiated variable decorrelation. In Proceedings of the 26th ACM Sigkdd International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 2185–2193. [Google Scholar]
- Zhang, X.; Cui, P.; Xu, R.; Zhou, L.; He, Y.; Shen, Z. Deep stable learning for out-of-distribution generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 5372–5382. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Monti, R.P.; Zhang, K.; Hyvärinen, A. Causal discovery with general non-linear relationships using non-linear ica. In Proceedings of the Uncertainty in Artificial Intelligence, PMLR, Tel Aviv, Israel, 22–25 July 2019; pp. 186–195. [Google Scholar]
- Clayton, P.; Davies, P. The Re-Emergence of Emergence: The Emergentist Hypothes; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Kim, J. Physicalism, or Something Near Enough; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Zhang, Z.; You, Y.Z. Observing Schrödinger’s Cat with Artificial Intelligence: Emergent Classicality from Information Bottleneck. arXiv 2023, arXiv:2306.14838. [Google Scholar]
- Glymour, C.; Zhang, K.; Spirtes, P. Review of causal discovery methods based on graphical models. Front. Genet.2019, 10, 524. [Google Scholar] [CrossRef] [PubMed]
- Zanga, A.; Ozkirimli, E.; Stella, F. A survey on causal discovery: Theory and practice. Int. J. Approx. Reason. 2022, 151, 101–129. [Google Scholar] [CrossRef]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. The backbone of the climate network. Europhys. Lett. 2009, 87, 48007. [Google Scholar] [CrossRef]
- Kalisch, M.; Bühlman, P. Estimating high-dimensional directed acyclic graphs with the PC-algorithm. J. Mach. Learn. Res. 2007, 8, 613–636. [Google Scholar]
- Zheng, X.; Aragam, B.; Ravikumar, P.K.; Xing, E.P. Dags with no tears: Continuous optimization for structure learning. Adv. Neural Inf. Process. Syst. 2018, 31, 9472–9483. [Google Scholar]
- Zhu, S.; Ng, I.; Chen, Z. Causal discovery with reinforcement learning. arXiv 2019, arXiv:1906.04477. [Google Scholar]
- Rantanen, K.; Hyttinen, A.; Järvisalo, M. Learning optimal cyclic causal graphs from interventional data. In Proceedings of the International Conference on Probabilistic Graphical Models, PMLR, Skørping, Denmark, 23–25 September 2020; pp. 365–376. [Google Scholar]
- Zhang, Z.; Zhao, Y.; Liu, J.; Wang, S.; Tao, R.; Xin, R.; Zhang, J. A general deep learning framework for network reconstruction and dynamics learning. Appl. Netw. Sci. 2019, 4, 110. [Google Scholar] [CrossRef]
- Pamfil, R.; Sriwattanaworachai, N.; Desai, S.; Pilgerstorfer, P.; Georgatzis, K.; Beaumont, P.; Aragam, B. Dynotears: Structure learning from time-series data. In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Palermo, Italy, 26–28 August 2020; pp. 1595–1605. [Google Scholar]
- Vowels, M.J.; Camgoz, N.C.; Bowden, R. D’ya like dags? a survey on structure learning and causal discovery. ACM Comput. Surv. 2022, 55, 1–36. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, L.; Xiao, T.; Li, Z.; Suo, J.; He, K.; Dai, Q. CUTS+: High-dimensional Causal Discovery from Irregular Time-series. arXiv 2023, arXiv:2305.05890. [Google Scholar]
- Wang, D.; Chen, Z.; Ni, J.; Tong, L.; Wang, Z.; Fu, Y.; Chen, H. Hierarchical graph neural networks for causal discovery and root cause localization. arXiv 2023, arXiv:2302.01987. [Google Scholar]
- Zhang, Q.; Zhang, C.; Cheng, S. Wavelet Multiscale Granger Causality Analysis Based on State Space Models. Symmetry 2023, 15, 1286. [Google Scholar] [CrossRef]
- Fan, C.; Wang, Y.; Zhang, Y.; Ouyang, W. Interpretable Multi-Scale Neural Network for Granger Causality Discovery. In Proceedings of the ICASSP 2023-2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar]
- Haugen, R.A.; Skeie, N.O.; Muller, G.; Syverud, E. Detecting emergence in engineered systems: A literature review and synthesis approach. Syst. Eng. 2023, 26, 463–481. [Google Scholar] [CrossRef]
- O’toole, E.; Nallur, V.; Clarke, S. Decentralised detection of emergence in complex adaptive systems. ACM Trans. Auton. Adapt. Syst. (TAAS) 2017, 12, 1–31. [Google Scholar] [CrossRef]
- O’Toole, E.; Nallur, V.; Clarke, S. Towards decentralised detection of emergence in complex adaptive systems. In Proceedings of the 2014 IEEE Eighth International Conference on Self-Adaptive and Self-Organizing Systems, London, UK, 8–12 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 60–69. [Google Scholar]
- Pazho, A.D.; Noghre, G.A.; Purkayastha, A.A.; Vempati, J.; Martin, O.; Tabkhi, H. A Survey of Graph-based Deep Learning for Anomaly Detection in Distributed Systems. arXiv 2022, arXiv:2206.04149. [Google Scholar] [CrossRef]
- Liu, R.; Wu, Z.; Yu, S.; Lin, S. The emergence of objectness: Learning zero-shot segmentation from videos. Adv. Neural Inf. Process. Syst. 2021, 34, 13137–13152. [Google Scholar]
- Chang, A.Y.; Biehl, M.; Yu, Y.; Kanai, R. Information closure theory of consciousness. Front. Psychol. 2020, 11, 1504. [Google Scholar] [CrossRef]
- Liu, Z.; Tegmark, M. Machine learning hidden symmetries. Phys. Rev. Lett. 2022, 128, 180201. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G.; Koch, C. Consciousness: Here, there and everywhere? Philos. Trans. R. Soc. B Biol. Sci. 2015, 370, 20140167. [Google Scholar] [CrossRef] [PubMed]
- Walker, S.I. Top-down causation and the rise of information in the emergence of life. Information 2014, 5, 424–439. [Google Scholar] [CrossRef]
- Elder-Vass, D. The Causal Power of Social Structures: Emergence, Structure and Agency; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory: From consciousness to its physical substrate. Nat. Rev. Neurosci. 2016, 17, 450–461. [Google Scholar] [CrossRef]
- Holland, J.H. Hidden order. In Business Week-Domestic Edition; Addison-Wesley: Boston, MA, USA, 1995; p. 21. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Adamatzky, A.; Chen, G.; Bazzan, A.L.C.; Brasil, R.; Burguillo, J.C.; Corchado, E.; Davendra, D.; Lampinen, J.; Middendorf, M.; Ott, E.; et al. Emergence, Complexity and Computation; Springer: Berlin/Heidelberg, Germany, 2022; p. 10624. [Google Scholar]
- Kreyssig, P.; Dittrich, P. Emergent control. In Organic Computing—A Paradigm Shift for Complex Systems; Springer: Basel, Switzerland, 2011; pp. 67–78. [Google Scholar]
- Mitchell, M.; Hraber, P.; Crutchfield, J.P. Revisiting the edge of chaos: Evolving cellular automata to perform computations. arXiv 1993, arXiv:adap-org/9303003. [Google Scholar]
(参考文献可上下滑动查看)
Entropy 因果与复杂系统特刊征稿中
复杂系统无处不在。系统复杂性的一个原因是,大型系统中不同层次上广泛存在纠缠的因果结构。在复杂系统中,因果关系可能是涌现的,这意味着如果对系统进行适当的粗粒化操作,那么更强的因果关系可能只在宏观层面而不是微观层面观察得到。更进一步,自上而下的因果关系,即系统中的宏观状态变量影响微观状态变量,也可以在活系统或社会系统中观察到。
然而,我们如何从一个复杂系统的原始数据中发现这些错综复杂的因果结构并识别因果涌现,以及如何利用这些因果机制推断系统未来的状态和演化,这些都是重要而又困难的问题。机器学习、互信息分解、因果推断等新兴技术将为我们提供新的解决方案。
Entropy 杂志 Causality and Complex Systems 特刊目前在持续征稿中,欢迎对相关话题感兴趣的研究者投稿,会议文章也可投稿。
主要信息如下:
期刊:Entropy (ISSN 1099-4300)
栏目:复杂性特刊
主题:因果与复杂系统(Causality and Complex Systems)
征稿截止日期:2024年9月24日
通过以下链接进入官网查看更多信息:https://www.mdpi.com/journal/entropy/special_issues/causality_complex_systems
因果涌现社区
跨尺度、跨层次的涌现是复杂系统研究的关键问题,生命起源和意识起源这两座仰之弥高的大山是其代表。因果涌现理论、机器学习重整化技术、信息论或信息分解等近年来新兴的理论与工具,有望破解复杂系统的涌现规律。
集智俱乐部因果涌现读书会目前已经进行了四季。第一季读书会系统地梳理了因果涌现的概念,以及它与Sloopy Model、复杂性阈值、自指等概念之间的联系,也探讨了因果涌现理论在复杂网络、机器学习中的应用。参看:因果涌现读书会启动:连接因果、涌现与自指——跨尺度动力学与因果规律的探索。
第二季读书会探讨了涌现、因果科学和机器学习三大主题的融合,包括信息论拓展、因果涌现理论、因果表示学习、多尺度机器学习动力学建模。请参看:因果、涌现与机器学习:因果涌现读书会第二季启动。
第三季读书会进一步围绕因果涌现的核心问题「因果涌现的定义」以及「因果涌现的辨识」进行深入学习和讨论,对 Erik Hoel 提出的 Causal Emergence,Causal Geometry 等因果涌现的核心理论进行探讨和剖析,并详细梳理其中涉及到的方法论,包括从动力学约简、隐空间动力学学习等其他领域中学习和借鉴相关的研究思路,最后探讨因果涌现的应用,包括基于生物网络、脑网络或者涌现探测等问题展开扩展,发掘更多的实际应用场景。请参看:因果涌现读书会第三季启动:深入多尺度复杂系统核心,探索因果涌现理论应用
第四季读书会主题是「新信息论:从分解到整合」,旨在重点梳理信息分解与整合信息论的相关研究。请参看:新信息论:从分解到整合|因果涌现读书会第四季启动。
因果涌现社区由集智俱乐部通过系列因果涌现读书会孕育孵化,旨在促进学术交流和科学创新,聚焦于破解复杂科学的圣杯问题,为国内学者和科学爱好者提供一个共享和探索的平台,推动科学研究的发展。
集智科学研究中心
集智科学研究中心是门头沟民政局批准成立、门头沟科信局主管的民办非企业,致力于营造跨学科探索小生境,催化复杂性科学新理论。集智研究中心长期关注复杂科学中的核心问题,如涌现、因果、自指、意识、生命起源等等,并充分结合人工智能机器学习技术尝试解决这些问题。目前已有13篇文章发表于国际期刊,其中包括一篇因果涌现的综述和一篇生命起源的综述。这里的文章大部分产生于集智社区读书会。
部分研究成果报道:
访问集智科学研究中心网站了解详情:www.research.swarma.org/research
推荐阅读
1. Entropy 因果与复杂系统特刊:从自上而下因果到闪烁涌现2. 什么是涌现?人工智能给你答案3. 涌现、因果与自指——“因果涌现”理论能否破解生命与意识之谜4. 科学能解释自由意志吗?4. 张江:第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 龙年大运起,学习正当时!解锁集智全站内容,开启新年学习计划6. 加入集智,一起复杂!
点击“阅读原文”,访问集智科学研究中心



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


