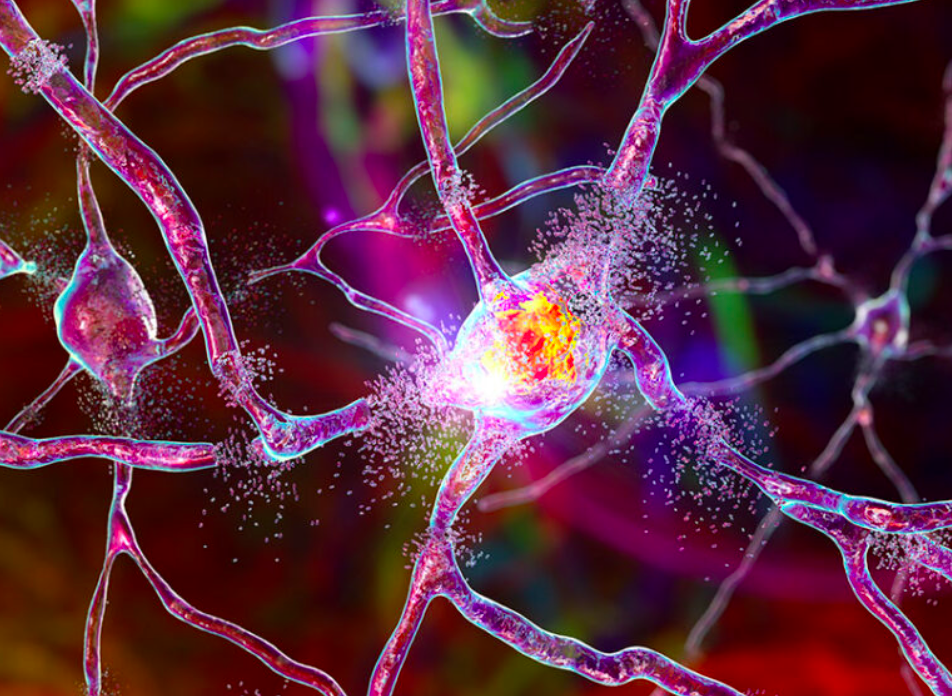
引言
哺乳动物的大脑由大量神经元组成,其神经活动表现出复杂和多层次的动态特征。在神经元层面,随机耦合的兴奋神经元和抑制神经元组成的神经回路在兴奋和抑制之间保持平衡(兴奋-抑制平衡);而集体神经活动则表现为具有无标度特征的神经雪崩(可通过神经临界性解释)。2024年1月发表于 The Neuroscientist 的最新综述文章深入研究了大脑中的兴奋-抑制平衡和神经临界性,发现了神经网络在静默和振荡状态之间的微妙转换,并揭示了这种平衡如何使大脑保持灵活性和稳定性,响应这个不断变化的世界。这种由微观到宏观,由单个神经元到整个神经网络的精妙互动,构成了我们感知、思考和行动的基础。本文是集智俱乐部「计算神经科学」读书会成员董金宇撰写的解读文章,由论文作者杨杼达、周昌松老师审校定稿,周昌松老师是「计算神经科学」读书会发起人之一。
集智俱乐部联合国内外多所知名高校的专家学者发起「计算神经科学」读书会,涵盖复杂神经动力学、神经元建模与计算、跨尺度神经动力学、计算神经科学与AI的融合四大模块,并希望探讨计算神经科学对类脑智能和人工智能的启发。读书会从2024年2月22日开始,每周四19:00-21:00进行,持续时间预计10-15周,欢迎感兴趣的朋友报名参与,深入梳理相关文献、激发跨学科的学术火花!
研究领域:计算神经科学,神经系统建模,兴奋-抑制平衡,神经临界性,无标度雪崩 董金宇 | 作者杨杼达,周昌松 | 审校
董金宇 | 作者杨杼达,周昌松 | 审校
 论文题目:Excitation–Inhibition Balance, Neural Criticality, and Activities in Neuronal Circuits论文地址:https://journals.sagepub.com/doi/10.1177/10738584231221766论文作者:梁俊豪,杨杼达,周昌松
论文题目:Excitation–Inhibition Balance, Neural Criticality, and Activities in Neuronal Circuits论文地址:https://journals.sagepub.com/doi/10.1177/10738584231221766论文作者:梁俊豪,杨杼达,周昌松
目录
0. 引言
1. 神经系统的数学建模
2. 兴奋-抑制平衡:理解单个神经元活动随机性的关键
3. 神经临界性:集体神经活动的无标度雪崩
4. 兴奋-抑制平衡与神经临界性的统一
5. 结语
0. 引言
哺乳动物的大脑有大量神经元,它们在广泛的空间和时间尺度上表现出多种复杂的电生理活动模式。了解这种复杂性的起源和动力学机制对于理解大脑功能和行为、开发大脑疾病疗法以及设计大脑启发智能系统至关重要。
从单个神经元到局部回路中的集体神经振荡,复杂的神经活动可在不同层次上观察到。
1. 在微观尺度上,单个神经元动作电位(图 1A)形成的脉冲是随机和不规则的(图 1B)。
2. 在中观尺度上,部分同步(附录3)的神经元的集群脉冲串联成神经雪崩(附录2),其大小和持续时间各不相同。
3. 在神经网络层面观察到的神经元群体活动(如局部场电位 LFP)展现出了具有广谱分布频率的振荡。
最近的实验和理论研究表明,兴奋-抑制平衡(Excitation–Inhibition Balance)和神经临界性(Neural Criticality) 是这些复杂神经活动背后的的两种可能机制(图 1C)。
在本文中,我们首先回顾神经网络的基本数学建模,然后引入兴奋抑制平衡的概念用于解释单个神经元不规则脉冲。其次,我们介绍神经临界性与无尺度雪崩的意义和功能。最后,我们介绍将这两种机制整合在一起的最新研究。通过结合兴奋-抑制神经回路与突触动力学(图 1C),对局部回路中神经元活动从自发到刺激-反应动力学的多层次复杂性有了更统一的认识。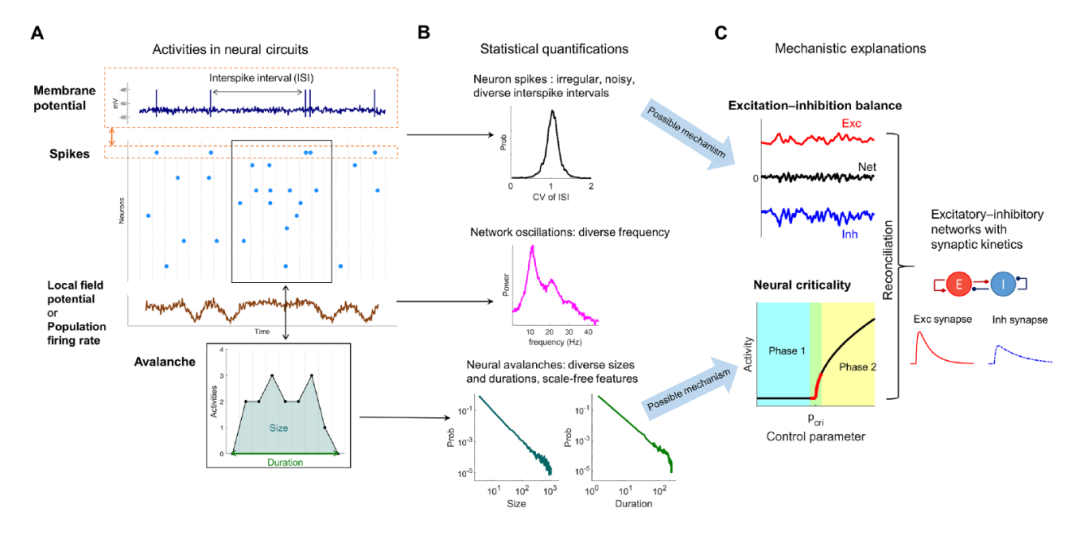 图1:神经回路中的活动(A)、其统计特征(B)以及可能的机理解释(C)。
图1:神经回路中的活动(A)、其统计特征(B)以及可能的机理解释(C)。
1. 神经系统的数学建模
神经元是大脑中的基本单位,它们通过电信号和化学物质相互沟通。每个神经元由细胞体、树突和轴突组成。树突接收信号,轴突发送信号。
- 单神经元
计算神经科学中常见的单神经元简化模型可以用以下公式表示,其中h表示输入;v表示神经元膜电位;输出简化为v的函数(激活函数 activation function)。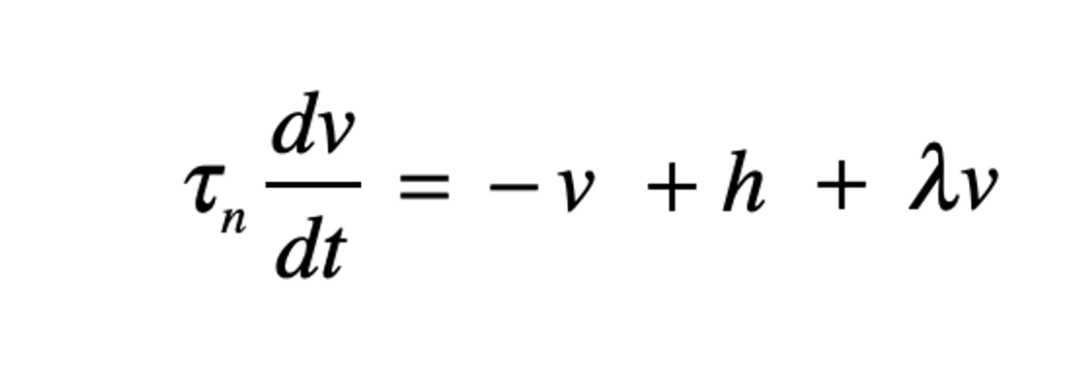 图2为一个自反馈神经元(为了简化,此处激发函数 y=λν为线性,λ为连接强度)。取决于λ的大小不同,这个神经元受到刺激后的状态可以是稳定、临界稳定或者非稳定。
图2为一个自反馈神经元(为了简化,此处激发函数 y=λν为线性,λ为连接强度)。取决于λ的大小不同,这个神经元受到刺激后的状态可以是稳定、临界稳定或者非稳定。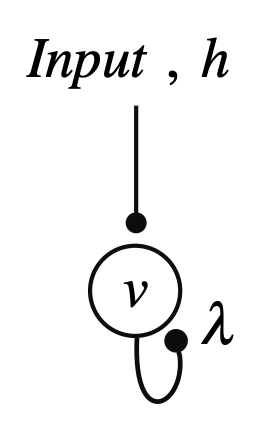
图2A:神经元简化图
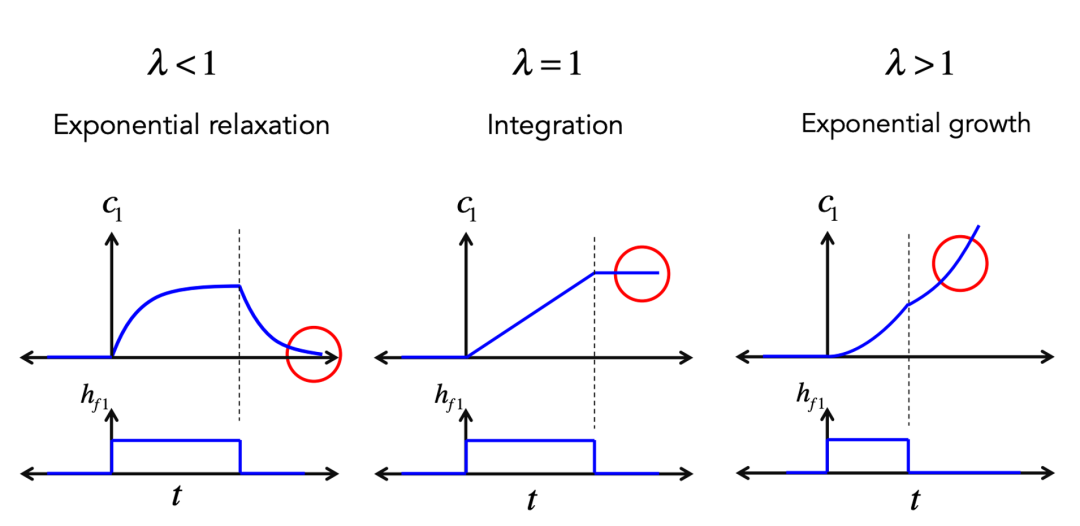
图2B:单神经元自反馈强度不同,受到刺激后的反应也不同。cr. MIT9.40
- 神经网络
当神经元不止一个,神经元相互连接构成一个神经网络(图3),神经元之间的连接强度可以用权重矩阵M来表示。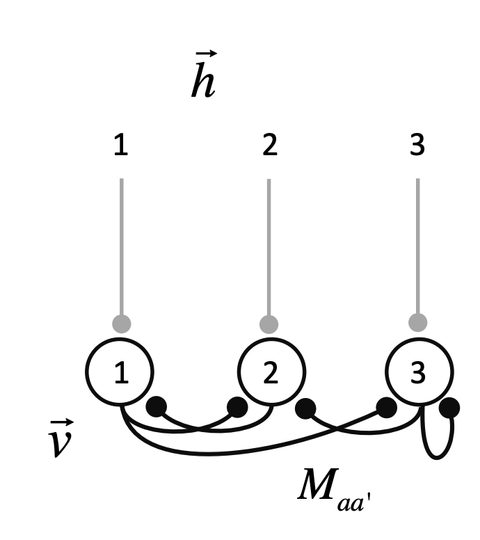 图3:神经网络示意图
图3:神经网络示意图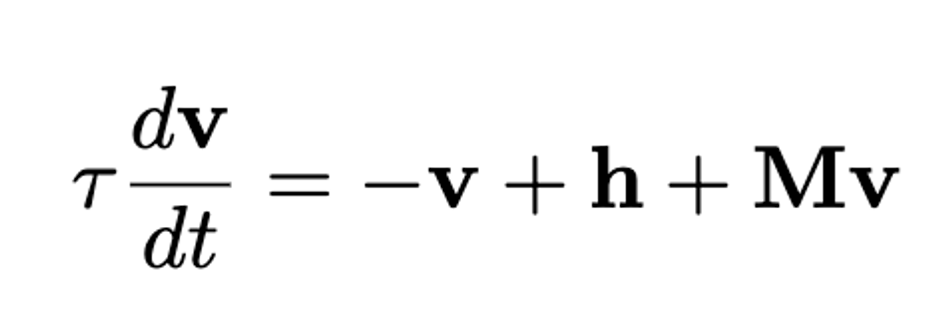
该神经网络由上面的公式表达,其中向量v表示所有神经元的膜电位,向量h表示每个神经元收到的输入,M表示神经元之间的连接强度。根据M的不同,该神经网络会呈现出稳定(asymptotically stable)、非稳定(unstable)或临界稳定(marginally stable)。
下面这个例子可以辅助理解临界状态:对于图4左图中由2个神经元组成的神经网络,系统有两个状态(两个平衡点)被虚线分开,分别位于左上角 (-1, 1) 和右下角 (1, -1)。当任意时刻系统位于左上的某个点例如(-1,0),系统会自发的向 (-1, 1) 运动(右下角同理),因此我们称这两个稳定平衡点为两个吸引子(Attactor)。如果系统保持在虚线附近,不被任何一个吸引子捕获,可以理解为系统运行在临界状态。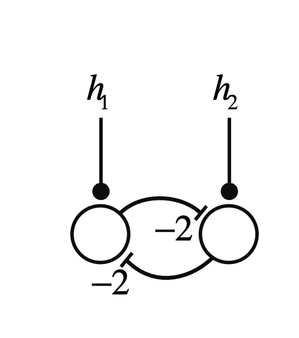
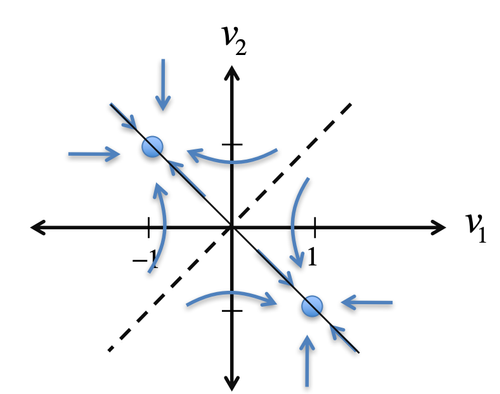
图4. 2个神经元组成的神经网络的临界状态示意图。
2. 兴奋-抑制平衡:
理解单个神经元活动随机性的关键
在神经科学中,“E”通常代表兴奋性(Excitatory)神经元,而“I”代表抑制性(Inhibitory)神经元。这两种类型的神经元在大脑中发挥着基本而不同的作用。
- 兴奋性神经元通过其活动促进(或增加)其他神经元的电活动。当兴奋性神经元向其他神经元传递信号时,它们使接收神经元更容易产生动作电位(也就是神经元的“激发”)。这种影响通常通过释放诸如谷氨酸等神经递质来实现。
- 抑制性神经元与兴奋性神经元相反,功能是减少其他神经元的电活动。当抑制性神经元向其他神经元发送信号时,它们使接收神经元更难产生动作电位。这种影响通常是通过释放如γ-氨基丁酸(GABA)等神经递质来实现的。
对于图3神经网络,兴奋性神经元ae伸向其他神经元的所有突触都是兴奋性的,连接强度Maae>0。抑制性神经元ai对应连接强度Maai<0。则意味着从a’到a之间没有突触的连接。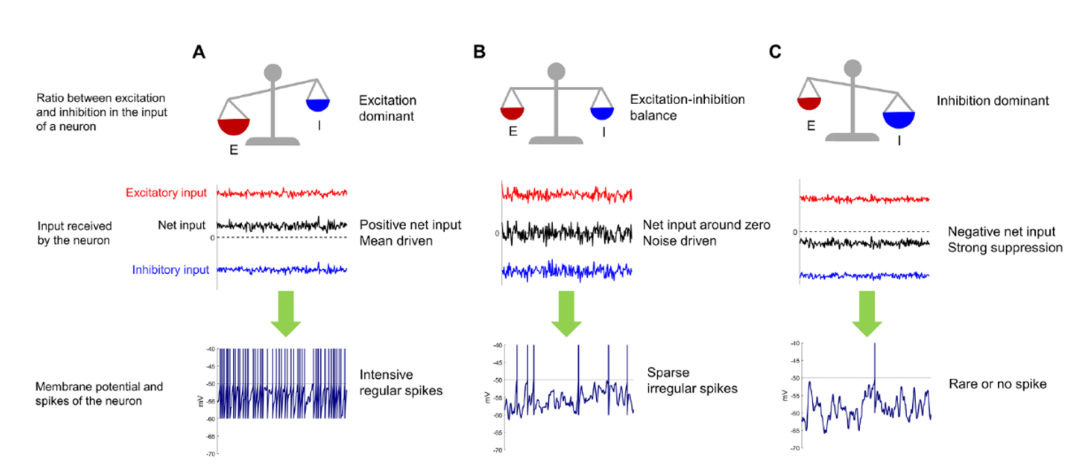 图5:兴奋-抑制平衡与不平衡的神经活动对比
图5:兴奋-抑制平衡与不平衡的神经活动对比
大脑皮层神经元活动表现出固有的“嘈杂性”,其特征是不规则的神经元脉冲类似于泊松随机过程。这导致了神经回路的随机性,挑战了我们对大脑功能的理解。最初由弗雷斯维克(Vreeswijk)和桑波林斯基(Sompolinsky)提出的兴奋-抑制平衡(Excitatory-Inhibitory Balance)理论为解释这一现象提供了一个框架[1]。根据 E-I 平衡理论,由随机耦合的兴奋神经元和抑制神经元组成的神经回路可以保持兴奋和抑制之间的平衡,从而导致神经元平均接收到的净输入为零。这种状态导致神经元因波动而随机发放,但不会过度兴奋或抑制。
兴奋抑制平衡对于大脑的正常功能至关重要。这种平衡确保神经活动既不过度兴奋,导致像癫痫这样的异常状态,也不过度抑制,导致功能低下或意识丧失。通过精确调节兴奋性和抑制性输入的相对强度,大脑能够有效地处理信息、维持正常的感觉、思维和运动功能,以及保持情绪稳定。同时兴奋抑制平衡也有助于高效的神经编码和信息处理,说明它在高效、经济的大脑运作中的重要作用。
这种平衡已在不同脑区和物种中得到证实,表明兴奋性和抑制性输入通常成正比,从而保持了功能的稳定性。神经生物学实验通过观察不同皮层区域的突触电流[2-4]证实了兴奋-抑制平衡。还有实验证据为兴奋抑制平衡提供了解剖学基础[5-6],突出了它在维持健康神经功能和动态方面的重要性。
3. 神经临界性:集体神经活动的无标度雪崩
兴奋-抑制平衡理论是理解单个神经元活动随机性的关键,但它并不能完全概括神经回路中神经元之间的相关活动。因此有必要对集体神经活动(collective neural activities)进行更深入的理论探索,这恰好可以应用统计物理学中临界性的概念。
临界性描述了系统不同动态状态之间的变化。神经回路的临界性会导致神经活动的雪崩表现出无标度(幂率)特性(图6)。本文关注由临界性引发的无标度雪崩的功能意义,而不探讨神经系统究竟是否处于临界态。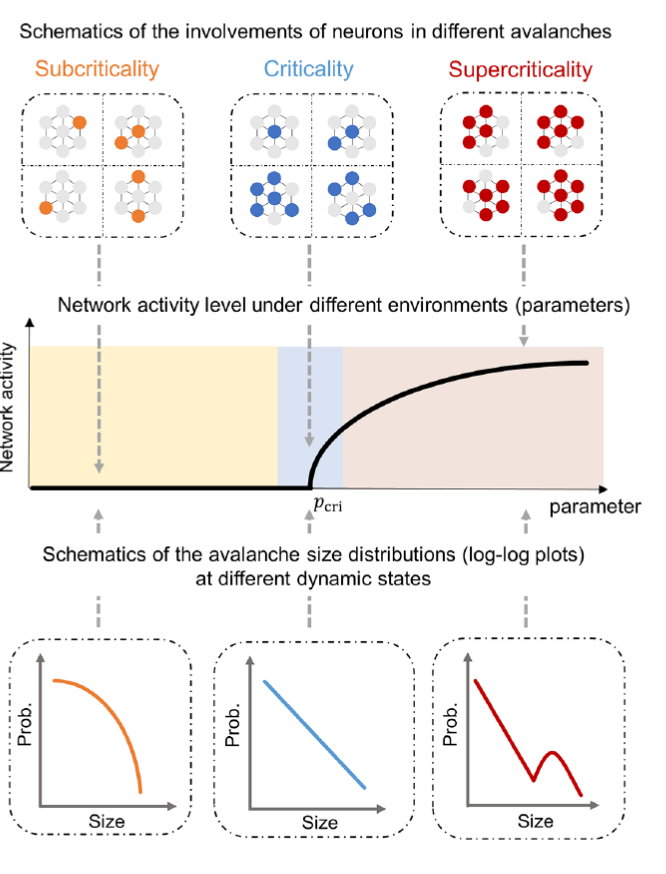
图6: 亚临界,临界,超临界状态神经雪崩具有不同的统计学性质。其中只有临界状态的雪崩呈现无标度性。
从历史上看,无标度神经雪崩最早是在大鼠大脑皮层培养物中观察到的[7],这是被视为临界状态的标志。这些无标度雪崩在不同物种和大脑状态下被观察到,强调了临界状态神经活动的广泛性。关于无标度雪崩的产生,论文中有更详细的理论解释,此处略过。
临界性在认知过程中的作用
- 它能最大限度地扩大动态范围,使神经元在各种刺激强度下都能做出最佳反应[8]。临界状态还能促进一系列神经动态变化,增强大脑的功能多样性和信息容量[9]。有趣的是,不同的研究表明,调谐到临界状态的神经回路可以获得更好的刺激辨别力和反应灵敏度[10]。
- 大脑在临界状态下运行允许模块化网络实现“少即是多”的效果[11],通过使用更少的材料和代谢能量成本(例如更短的网络连接长度和较低的脉冲频率)实现更多的功能价值(例如响应灵敏度)。这表明临界性可以指导开发高效的计算算法。
- 临界性的概念已从微观(少量神经元)扩展到宏观(大脑),揭示了不同大脑区域存在异质临界状态的可能性(例如,不同脑区的局部神经回路可能更接近或远离临界状态)[10,12]。这种异质性可能有助于灵活的信息处理[10,12],最大限度地提高功能多样性[13],增加皮层区域之间的信息传输[14]。
- 最后,单个神经元的反应波动可被视为神经元树突中集体离子通道活动诱发的雪崩。这种在单神经元尺度上定义的雪崩显示出临界特征[15],有利于树突计算[16]。然而,目前还不清楚在不同尺度上观察到的雪崩是否以及如何相互关联。
4. 兴奋-抑制平衡与神经临界性的统一
兴奋-抑制平衡和神经临界性是研究神经活动的两个方面,但二者其实密切相关。
-
单个神经元的脉冲产生具有随机性
- 集体神经活动的雪崩的大小和时长具有可变性和无标度特性
已经有许多研究从生理[17-20],人脑电图[21]和计算模拟[22]等多个角度指出,神经临界性仅在电路处于E-I平衡状态时才会保持。
最近的一项理论研究表明[23],在从异步状态过渡到同步状态(附录3)的过程中,不规则神经脉冲所反映的兴奋-抑制平衡与无标度雪崩所代表的神经临界性之间可以被统一。这项研究通过在兴奋-抑制平衡的神经网络中纳入符合生物现实的突触动力学(excitatory–inhibitory networks with synaptic kinetics)[24,25],扩展了整合-发放神经元模型(integrate-and-fire neurons)下的经典理论[26]。
兴奋性和抑制性突触之间相对时间尺度的变化可以在维持兴奋-抑制平衡的情况下改变神经振荡的性质。快速作用的抑制性突触会促进紧平衡(tight balance),导致集体脉冲事件非常罕见,而缓慢的抑制则会导致松平衡(loose balance),产生更大的集体脉冲和超临界雪崩。速度适中的抑制会导致大小不一的雪崩,从而表现出临界特性。在紧平衡状态下,神经元接收的兴奋信号大体上会被抑制信号所抵消,从而在局部产生由噪声驱动的不规则脉冲,但整体不体现出随机性。这一理论表明E-I 平衡可以支持神经临界性的产生。然而,仍不清楚是什么决定了雪崩分布临界指数,需要进一步探索。
非线性动力学分析表明,延长抑制性突触的时间尺度会延迟抑制反馈,进而而引发霍普夫分岔,标志着神经元脉冲从异步过渡到稀疏同步。这种分岔从模型层面表明了临界性,并且与无标度神经学雪崩同时存在[23]。这种临界性,即在稳定和振荡状态之间的平衡,也可能源于脉冲相关性或网络连通性的增加。研究[28]证实了这一现象的普遍性,表明抑制强度的变化可以调节神经回路从临界状态到异步状态。
E-I平衡和神经临界性框架解释了神经回路如何对外部刺激做出反应,这是神经系统的一项关键功能。E-I平衡允许对刺激做出线性和亚线性反应,而临界性则增强刺激编码,并在外部影响下保持电路临界状态。Liang 和 Zhou 的模型进一步证明,刺激-反应的可靠性和变异性的降低在临界状态下得到最佳维持,而不能在亚临界或超临界状态下保持[27]。因此,E-I 平衡时的神经临界状态可以帮助我们了解神经回路活动中观察到的两个看似矛盾的特征——灵敏性和可靠性[29]是如何形成的。
5. 结语
在探索大脑的奥秘这条漫长而复杂的旅程中,我们逐渐揭开了神经科学的一角——神经元之间的微妙平衡和它们如何响应这个不断变化的世界。通过深入研究E-I平衡和神经元的临界状态,科学家们不仅发现了神经网络在静默和振荡状态之间的微妙转换,而且还揭示了这种平衡如何使大脑保持灵活性和稳定性,同时对外界刺激做出精确的反应。
这些发现为我们提供了关于大脑如何处理信息、如何适应环境变化以及如何在稳定性与灵活性之间找到完美平衡的深刻洞见。它们让我们认识到,大脑的每一次响应,都是它不断自我调整、寻找平衡的结果。这种由微观到宏观,由单个神经元到整个神经网络的精妙互动,构成了我们感知、思考和行动的基础。
概念介绍
神经雪崩(Neural avalanch)神经雪崩可定义为活跃期内的一连串神经活动,由相邻的非活跃期隔开。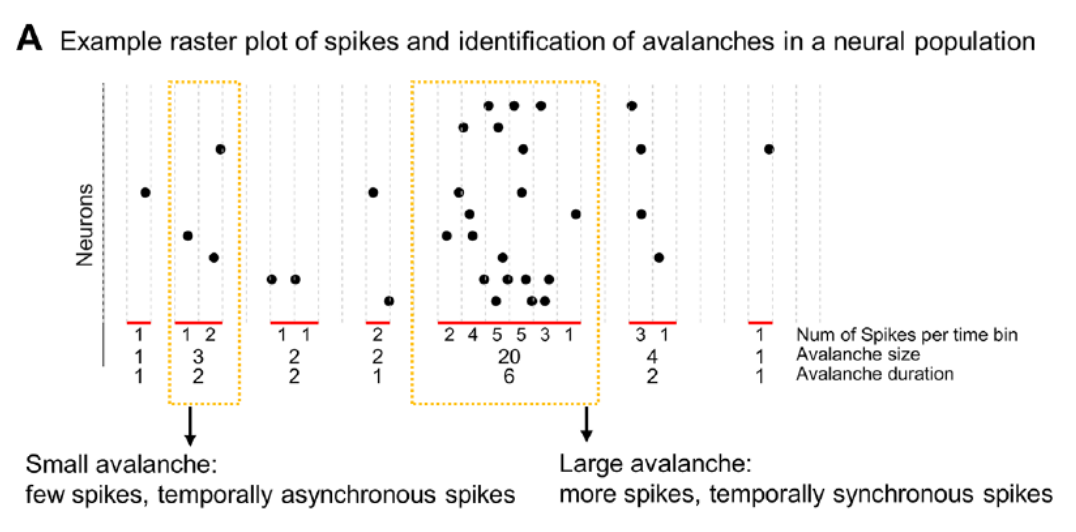
无标度(scale-free)无标度指神经雪崩的大小和时长呈幂律分布。
神经集群的异步状态和同步状态
1. 异步状态(Asynchronous state):在这种状态下,神经元的活动是不协调的,也就是说,各个神经元的动作电位的发放是在统计上独立的,没有明显的时间上的关联或同步性。这意味着,任何一个神经元在特定时间点发放动作电位的可能性并不依赖于其他神经元的活动状态。在异步状态下,尽管每个神经元的活动看似随机,但整个网络可以维持一种动态平衡,这主要得益于兴奋性和抑制性神经元之间的相互作用,即E-I平衡。
2. 稀疏同步发放状态(Sparsely synchronous spiking state):在这种状态下,神经元的活动开始展现出某种程度的协同性或同步性,但这种同步并不是全部神经元都同时活跃,而是小群体的神经元会展现出同步的发放模式。这种“稀疏”的同步意味着任何时刻只有部分神经元是同步活动的,而这些同步的神经元群体可以在网络中不断变化。这种稀疏的同步性可以帮助神经网络在保持整体稳定的同时,对特定的刺激或信息进行有效的编码和传递。
参考文献
- Van Vreeswijk C, Sompolinsky H. 1996. Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274:1724–6.
- Shu Y, Hasenstaub A, McCormick DA. 2003. Turning on and off recurrent balanced cortical activity. Nature 423:288.
- Xue M, Atallah BV, Scanziani M. 2014. Equalizing excitation inhibition ratios across visual cortical neurons. Nature 511:596.
- Okun M, Lampl I. 2008. Instantaneous correlation of excitation and inhibition during ongoing and sensory-evoked activities. Nat Neurosci 11:535.
- Liu G. 2004. Local structural balance and functional interaction of excitatory and inhibitory synapses in hippocampal dendrites. Nat Neurosci 7:373–9.
- Iascone DM, Li Y, Sümbül U, Doron M, Chen H, Andreu V, and others. 2020. Whole-neuron synaptic mapping reveals spatially precise excitatory/inhibitory balance limiting dendritic and somatic spiking. Neuron 106:566–78.
- Beggs JM, Plenz D. 2003. Neuronal avalanches in neocortical circuits. J Neurosci 23:11167–77.
- Kinouchi O, Copelli M. 2006. Optimal dynamical range of excitable networks at criticality. Nat Phys 2:348.
- Shew WL, Yang H, Yu S, Roy R, Plenz D. 2011. Information capacity and transmission are maximized in balanced cortical networks with neuronal avalanches. J Neurosci 31:55–63.
- Gollo LL. 2017. Coexistence of critical sensitivity and subcritical specificity can yield optimal population coding. J R Soc Interface 14:20170207.
- Liang J, Wang S-J, Zhou C. 2022. Less is more: wiring-economical modular networks support self-sustained firingeconomical neural avalanches for efficient processing. Natl Sci Rev 9:nwab102.
- Gollo LL, Copelli M, Roberts JA. 2016. Diversity improves performance in excitable networks. PeerJ 4:e1912.
- Wang R, Lin P, Liu M, Wu Y, Zhou T, Zhou C. 2019. Hierarchical connectome modes and critical state jointly maximize human brain functional diversity. Phys Rev Lett 123:38301.
- Fagerholm ED, Scott G, Shew WL, Song C, Leech R, Knöpfel T, and others. 2016. Cortical entropy, mutual information and scale-free dynamics in waking mice. Cereb Cortex 26:3945–52.
- Gal A, Marom S. 2013. Self-organized criticality in singleneuron excitability. Phys Rev E Stat Nonlinear Soft Matter Phys 88:062717.
- Gollo LL, Kinouchi O, Copelli M. 2013. Single-neuron criticality optimizes analog dendritic computation. Sci Rep 3:3222.
- Gautam SH, Hoang TT, McClanahan K, Grady SK, Shew WL. 2015. Maximizing sensory dynamic range by tuning the cortical state to criticality. PLoS Comput Biol 11:e1004576.
- Shew WL, Yang H, Petermann T, Roy R, Plenz D. 2009. Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J Neurosci 29:15595–600.
- Shew WL, Yang H, Yu S, Roy R, Plenz D. 2011. Information capacity and transmission are maximized in balanced cortical networks with neuronal avalanches. J Neurosci 31:55–63.
- Yang H, Shew WL, Roy R, Plenz D. 2012. Maximal variability of phase synchrony in cortical networks with neuronal avalanches. J Neurosci 32:1061–72.
- Meisel C, Schulze-Bonhage A, Freestone D, Cook MJ, Achermann P, Plenz D. 2015. Intrinsic excitability measures track antiepileptic drug action and uncover increasing/decreasing excitability over the wake/sleep cycle. Proc Natl Acad Sci U S A 112:14694–9.
- Larremore DB, Shew WL, Ott E, Sorrentino F, Restrepo JG. 2014. Inhibition causes ceaseless dynamics in networks of excitable nodes. Phys Rev Lett 112:138103.
- Liang J, Zhou T, Zhou C. 2020. Hopf bifurcation in mean field explains critical avalanches in excitation-inhibition balanced neuronal networks: a mechanism for multiscale variability. Front Syst Neurosci 14:580011. https://www. frontiersin.org/article/10.3389/fnsys.2020.580011
- Brunel N, Wang X-J. 2003. What determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J Neurophysiol 90:415–30.
- Yang DP, Zhou HJ, Zhou C. 2017. Co-emergence of multiscale cortical activities of irregular firing, oscillations and avalanches achieves cost-efficient information capacity. PLoS Comput Biol 13:e1005384.
- Van Vreeswijk C, Sompolinsky H. 1998. Chaotic balanced state in a model of cortical circuits. Neural Comput 10:1321–71.
- Liang J, Zhou C. 2022. Criticality enhances the multilevel reliability of stimulus responses in cortical neural networks. PLoS Comput Biol 18:e1009848.
- Li J, Shew WL. 2020. Tuning network dynamics from criticality to an asynchronous state. PLoS Comput Biol 16:1–16. http://dx.doi.org/10.1371/journal.pcbi.1008268
- Ebrahimi S, Lecoq J, Rumyantsev O, Tasci T, Zhang Y, Irimia C, and others. 2022. Emergent reliability in sensory cortical coding and inter-area communication. Nature 605:713–21.
(参考文献可上下滑动查看)
计算神经科学读书会
人类大脑是一个由数以百亿计的神经元相互连接所构成的复杂系统,被认为是「已知宇宙中最复杂的物体」。本着促进来自神经科学、系统科学、信息科学、物理学、数学以及计算机科学等不同领域,对脑科学、类脑智能与计算、人工智能感兴趣的学术工作者的交流与合作,集智俱乐部联合国内外多所知名高校的专家学者发起神经、认知、智能系列读书会第三季——「计算神经科学」读书会,涵盖复杂神经动力学、神经元建模与计算、跨尺度神经动力学、计算神经科学与AI的融合四大模块,并希望探讨计算神经科学对类脑智能和人工智能的启发。读书会从2024年2月22日开始,每周四19:00-21:00进行,持续时间预计10-15周,欢迎感兴趣的朋友报名参与,深入梳理相关文献、激发跨学科的学术火花!
详情请见:
推荐阅读
1. PNAS速递:神经网络异质性控制脉冲神经网络计算2. 神经元模型:从离子通道到计算3. 探索大脑临界性的理论基础:重新理解神经动力学4. 张江:第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 龙年大运起,学习正当时!解锁集智全站内容,开启新年学习计划6. 加入集智,一起复杂!
点击“阅读原文”,报名读书会



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


