
导语
上世纪90年代初,朗顿创造了“在混沌边缘计算”这个术语,并开始思考一个难题:系统的复杂性来源于何处。他的文字已经暗示这一迷思与信息理论的紧密关联。Joseph T. Lizier 在 2010 年从悉尼大学获得计算机科学博士学位,在他的博士论文《复杂系统中分布式计算的局部信息动力学》(The Local Information Dynamics of Distributed Computation in Complex Systems)中,接过朗顿提出的挑战,深入信息理论的基础,继续探讨分布式计算与系统复杂性的关系,真正用定量的指标来刻画复杂系统的涌现特征。在这若干年后,人们发现传统信息指标处理多元变量关系的力不从心,于是有了「因果涌现读书会第四季」提到的整合信息分解框架。它继承了 Lizier 的概念和思想,所以回过头来解读这篇博士论文会帮助我们对整合信息分解有更加深刻地理解。
我们计划用一系列共三篇文章解读 Lizier 的博士论文,第一篇文章《复杂系统研究为什么关注信息论?》中,我们介绍了复杂系统中存在着分布式计算,包括信息存储、信息转移和信息修正。今天这篇文章我们逐一介绍这三种不同的信息动力学和它们对应的局部信息指标,这套指标能够刻画和阐释元胞自动机里发生的涌现结构和分布式计算:在元胞自动机里,静态的粒子(闪烁体)进行着信息存储,动态的粒子(滑行体)进行着信息转移,而粒子的碰撞则是在进行信息修正。在更为复杂的元胞自动机比如生命游戏中,这种涌现出来的粒子甚至可以作为基本的运算单位,用来构建图灵机,模拟任意复杂的其他的计算过程。
关键词:复杂系统,信息论,分布式计算,信息动力学,元胞自动机,涌现 杨明哲 | 作者梁金 | 编辑
杨明哲 | 作者梁金 | 编辑
自朗顿提出“混沌边缘的计算”之后,科学家们开始关注信息论对复杂系统研究的价值。在复杂系统当中,每一个主体都在进行“无意识”地计算,根据某些输入,得到一些输出。这样的分布式计算在同一时刻发生在组成一个系统的所有个体身上,而且往往与主体间相互作用有关。计算的发生,带来信息的变化,可以被信息论的性质所捕获。
正如任何种类系统都受能量守恒定律的约束一样,信息论中也有严格成立的法则适用于所有的系统,无关乎你是振子网络、元胞自动机,还是蚁群、大脑。既然我们认为复杂系统的涌现与大量个体间相互作用有关,而个体间相互作用能反映在信息论指标里,那么自然会想到利用信息论指标帮助我们识别和阐释系统的涌现现象。
元胞自动机是一个体现分布式计算的经典案例,尤其是初等元胞自动机,人们对它的种类和性质已经有了充分的了解。看起来它似乎只是人为构建的模拟系统,但具有复杂系统共通的性质,而且非常简洁,有利于用来验证各个信息论指标的含义和作用。如果我们可以在初等元胞自动机上分析透彻涌现相关的信息论指标,那么就有充足的理论依据将这些指标拓展应用到更为复杂的实际系统当中。
在上一篇文章《复杂系统研究为什么关注信息论?》中,我们介绍了复杂系统中存在着分布式计算,包括信息存储、信息转移和信息修正。接下来我们逐一介绍这三种不同的信息动力学和它们对应的局部信息指标,主要以元胞自动机为案例,展示这些指标在实践中如何应用,帮助我们识别复杂系统涌现出的斑图。
1. 信息存储
信息存储在各种自然或人工的系统中广泛的存在。它指的是,一个变量或主体的历史序列中可以被用来预测其未来的信息量。研究信息存储最常见的指标便是过剩熵(excess entropy),如下式所示。
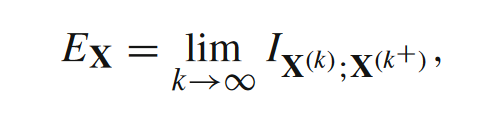
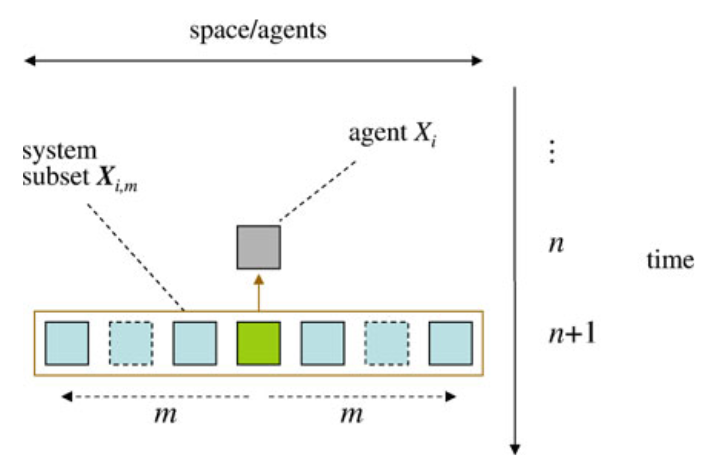
其中X(k)表示的是所有变量的k阶历史变量,相对应的,X(k+)表示k阶未来变量。k趋向于无穷大即意味着过剩熵度量的是所有历史变量和所有未来变量之间的互信息。在应用中,我们真正计算的是局部过剩熵(local excess entropy),如下式所示。
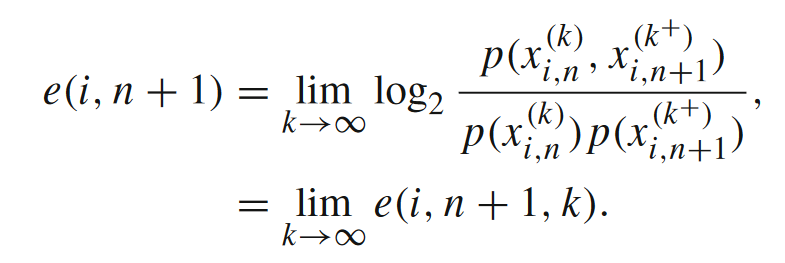
互信息度量的是变量间的关系,而局部互信息度量的则是事件之间的关系,互信息是局部互信息的期望值。某一个信息指标去除求期望的操作,得到的就是它的局部的指标。在上式中,我们会在接下来使用的是e(i,n+1,k),其中i表示主体的编号(比如元胞自动机中第i号元胞),n+1表示第n+1个时刻,而k则是我们追溯的历史和未来的长度。显然我们无法计算无穷多维变量事件的互信息,这里有一个权衡:如果k太小,则会丢失过多的信息,而如果k太大,对采样数量要求会比较高,计算压力大,所以在实践中我们需要选定一个合适的k。我们知道互信息本身是非负的,但局部互信息却有可能出现负值。负的局部互信息意味着观测者被误导,即当给定观测到的历史序列下,未来事件发生的概率比在没有任何条件下该事件发生的概率低。换句话说,历史的信息不但没有帮助观测者,反倒让观测者更难预测未来了。
在复杂系统中,斑图的出现往往跟特定的初始条件或环境有关,这种特定的事件会被求平均的互信息或其他诸如此类的信息指标所忽略。所以关注局部指标才能捕捉到这些斑图,只有局部的信息指标才能描述在每一个时间步上信息是如何运作的,即反映出信息动力学。目前,局部信息度量指标已经帮助我们对非线性系统的动力学提供很多洞察[1]。
回到过剩熵上来。它度量的是某一主体过去若干时刻与未来若干时刻所有的交互关系,如下图(a)所示。图中横轴表示空间,分布着一个个细胞即一个个主体。纵轴是时间,一般情况下某一主体的过去对未来会有影响,发生着信息存储的过程。相比于所有的未来时刻,在当下我们大多真正关心的其实是,只对于下一时刻的预测,我们会用到的信息,也就是活跃信息存储(active information storage),如图(b)所示。
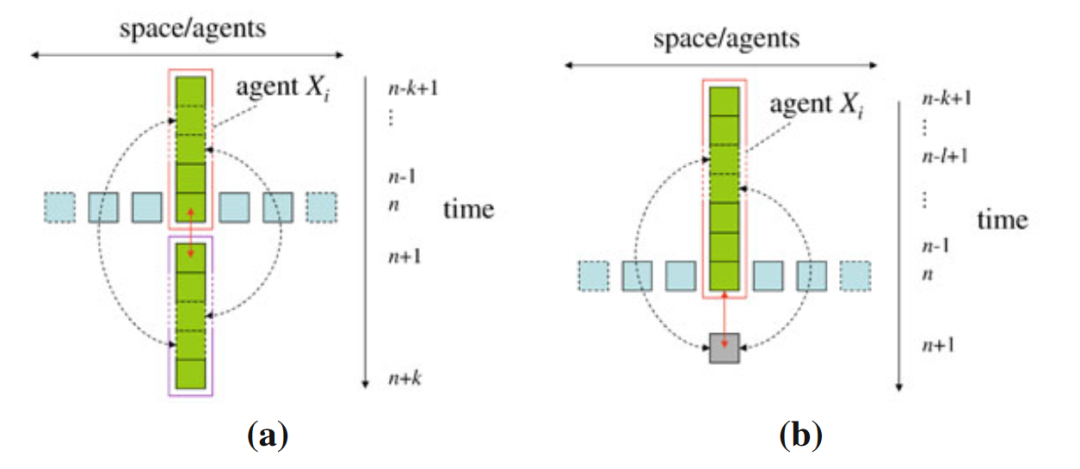
于是,能够度量信息存储的第二个指标出现了。活跃信息存储的表达式如下所示,其中X’表示下一时刻的变量。它也有对应的局部的表达方式,详情见下文的表格。
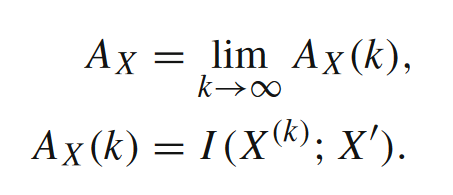
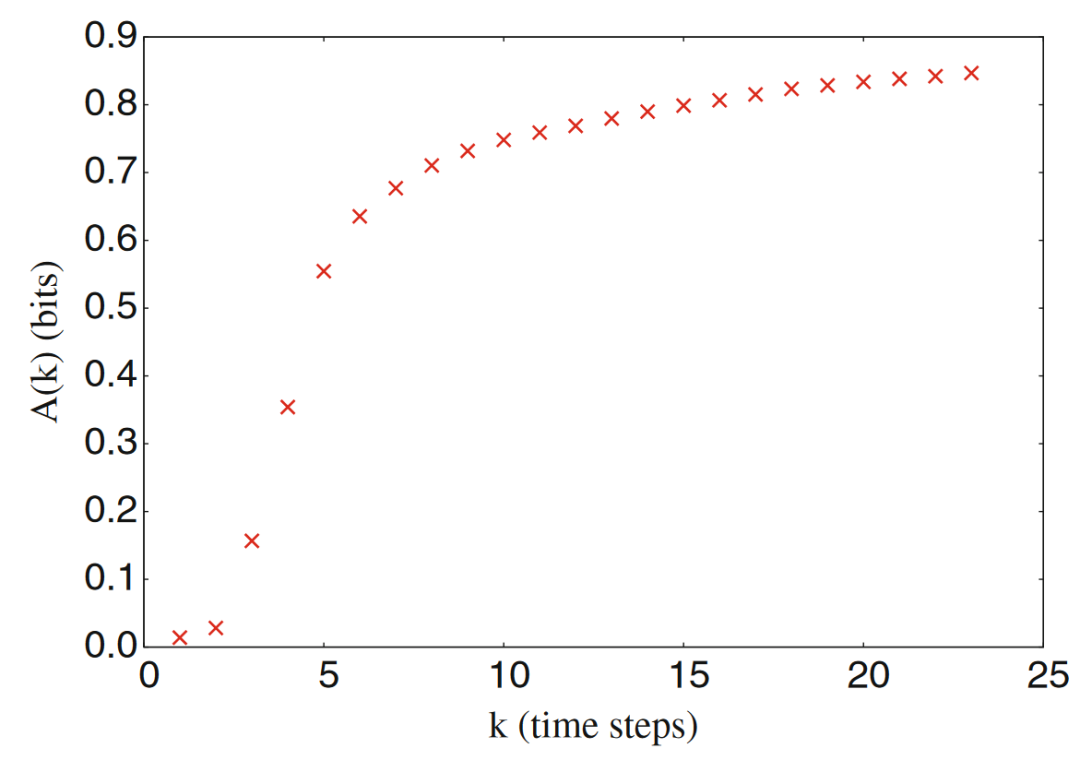
可以想见,随着k的取值增大,活跃信息存储应当会收敛于某一个上界,因为仅就下一时刻而言,不需要用到无穷多的信息。如下图所示,这是元胞自动机110号中随着k增大时活跃信息存储的变化曲线。
进一步我们可以引出第三个度量指标,熵率(entropy rate)。活跃信息存储本身还是一个互信息,度量的是历史对下一时刻变量消除的不确定性,而熵(全部的不确定性)减去互信息便是条件熵。已知历史的条件下,下一时刻历史的条件熵便是熵率,描述的是平均每个时刻相比于过去所增长的不确定性。数学语言描述如下,其中Hµ表示的就是熵率。
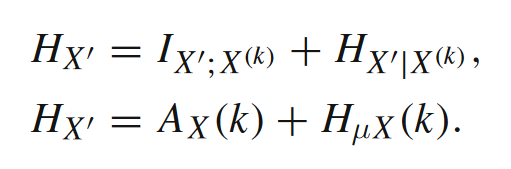
怎样理解这样的式子?正如James Crutchfield所认为(《计算力学:量化涌现的又一条路径》),复杂系统生成的时间序列就好比主体在世界中观察到的数据,其中有规律的、可以被主体利用的变化就是活跃信息存储所度量的;而其余没有规律的,无法从历史当中推断出来的随机性的变化就是熵率所度量的。把它们合在一起,便是时间序列在某一时刻蕴含的全部不确定性。当然熵率也有它局部的表达方式,这里就不详细展开了。至此,三种和信息存储有关的具体度量指标悉数登场,罗列在下表中。

接下来我们进入元胞自动机的世界,看看这些局部度量指标如何应用在具体场景中。我们首先来介绍一维元胞自动机中会出现的斑图。最普遍的是域(domain),它们往往作为背景在一个元胞自动机的二维时空变化图上成片成片地广泛存在(域在论文[2]中有形式化的定义)。两片域之间会存在边界,被定义为粒子(particle),在有的文献中也称作域墙(domain wall)。粒子有静态和动态之分。如果随着时间展开,某粒子只在特定的几个元胞上出现,那么它就是静态的粒子,也被称作闪烁体(blinker)。如果该粒子能够向周围邻居细胞转移,那么它就是动态的,也被称作滑行体(glider)。所有这些斑图都具有周期变化的特征。
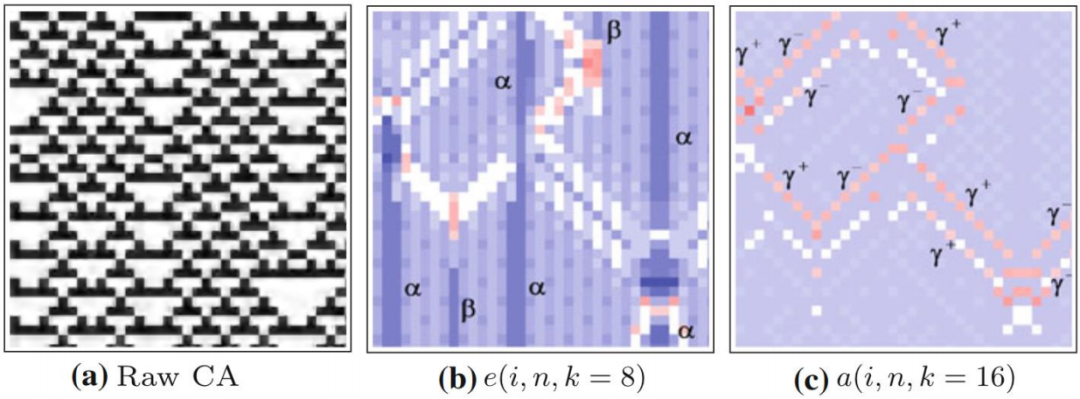
上图中的(a)展示了规则54的一维元胞自动机。横轴为空间,共有35个细胞,纵轴为时间,运行了35步。我们可以看到这张时空二维图上展示出来的各种图案。图(b)和(c)分别表示局部过剩熵和局部活跃信息存储的分布图,蓝色为正值,红色为负值。α和β两个字母标记了局部过剩熵值比较大的区域,识别出的图案是闪烁体。随着时间轴从上往下,闪烁体呈现出0-0-0-1的模式交替出现,而旁边呈现周期变化0-0-1-1和0-1的则是域。相比于活跃信息存储只能关注与下一时刻状态相关的周期规律,局部过剩熵可以度量所有k阶未来相关的周期规律(在该实验中k=8),所以度量粒子的值会更大,与其他没有粒子出现的区域区别更明显。
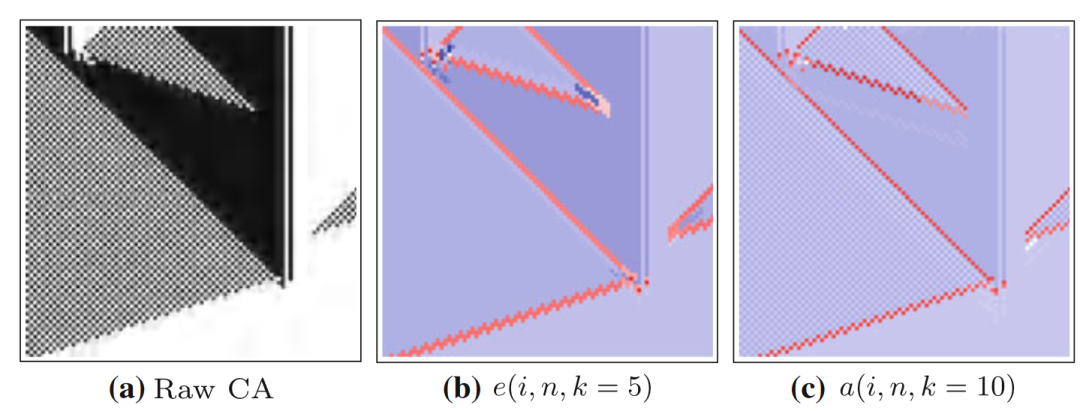
我们接着来看另一个元胞自动机,Φpar。它度量的是上一时刻一定范围内细胞‘0’和‘1’的占比,在本文实验中主体关注的范围大小便是r=3,展示了86个细胞的86个时间步。关于这种元胞自动机更详细的描述可以参见论文[3]。该元胞自动机清晰展示了两种不同的域,两个域之间有滑行体作为边界。相比于闪烁体(54号元胞自动机的α和β),域包含的信息存储量更小(哪怕周期长度相同,因为域只是重复自身,而粒子除了重复自身,存储的信息还包含了运动方向和两个域的转化),所以局部过剩熵的值就没有很大。我们可以设定一个阈值iB来区分这两个斑图,如果局部过剩熵小于这个阈值那么识别出来的就是域,大于阈值的话则是闪烁体。
读者不难发现图中还有出现负值的时候,这又意味着什么呢?其实,负的活跃信息存储可以用来捕捉滑行体,正如规则54元胞自动机图(c)中标注的γ区域。正如前文所述,当局部互信息出现负值时,说明历史状态对未来的预测起到了误导作用。不难想象,某一个元胞原本有自己固有的运作规律,可当它遭遇另一个从其他地方走来的滑行体时,原本的规律就被打破或者干扰了。如果仍使用历史经验来预测,反倒预测不准下一时刻的状态了,于是出现负的活跃信息存储。我们还会发现,局部过剩熵也会出现负值,但似乎比局部活跃信息存储的红色要浅很多。这是因为,如果一个滑行体走过来又立马离开了,那么对于当地的细胞而言,未来的若干时刻中只有部分时刻的状态会被误导,其余状态还可以使用自身的历史来预测。而局部过剩熵度量的是多个未来时刻,所以被误导的那一部分就被稀释或抵消掉了。可见,对于运动的图案来说,局部活跃信息存储是一个更为清晰的指标。
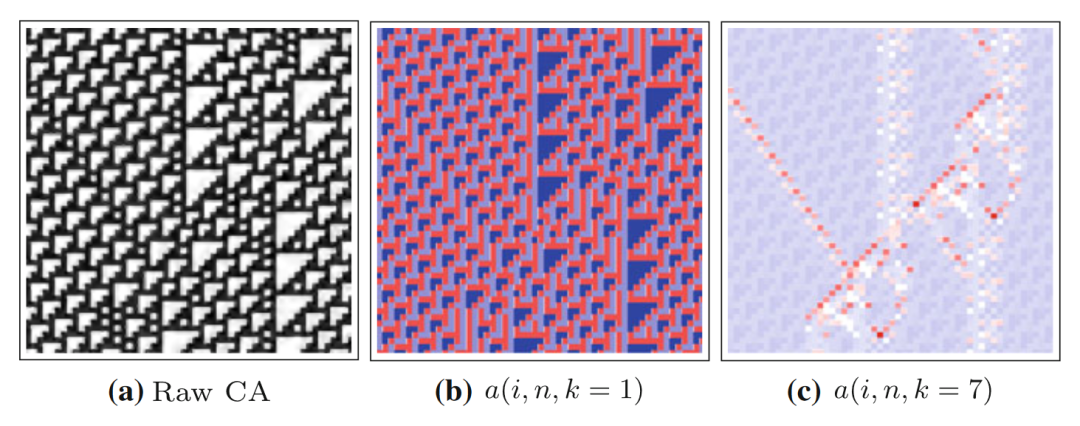
接下来我们对比一下不同k的选择会对度量结果有什么影响。下图展示了110号规则元胞自动机。相比于k=7,k=1的情况下丢失的信息更多,已经几乎无法识别出运动的粒子。所以在算力的允许下,k的取值越大越好。
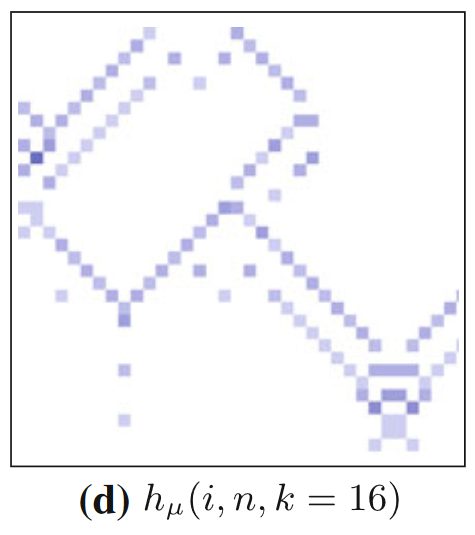
除了局部过剩熵和局部活跃信息存储,我们前面还提到了局部熵率,它能起到什么作用呢?根据前文中的表达式我们已知,某一时刻某一个元胞的熵等于局部的活跃信息存储和熵率之和。一般情况下,每个元胞的熵近似为1bit(0和1基本均匀分布),所以活跃信息存储和熵率存在反比的关系。于是,我们也可以用局部熵率(出现正值)来识别运动粒子。下图便是规则54的一维元胞自动机的局部熵率分布图。
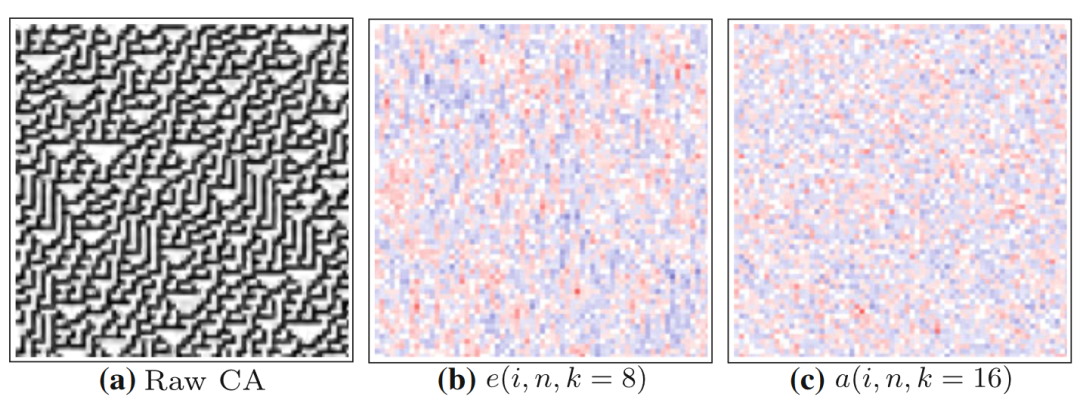
看完了正例,我们也来看一下反例,即什么时候没有信息存储的过程。比如下图所示的30号规则元胞自动机,局部过剩熵和局部活跃信息存储都没有呈现出清晰有指向的分布。事实上,这样的规则在分类中正属于混沌类型规则。
至此,我们来总结一下信息存储相关指标和对应的斑图。

2. 信息转移
信息转移是另一个复杂系统非线性行为的重要组成部分,广泛存在于包括鱼群行为转向波、晶体中固态相变、突触结构诱导等等真实系统行为当中。在这里,我们采用[4]中对信息转移的形式化定义:从一个源主体到一个目标主体的信息转移指的是,关于目标主体下一时刻状态的信息存在了源主体那里,但没有存在目标主体的历史当中。能够度量这一特性的最佳指标就是转移熵(transfer entropy)了,如下式所示。
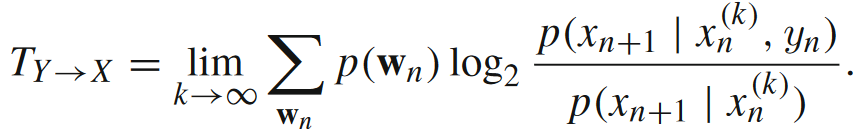
该式子中,Y是源主体,X是目标主体,p(wn)表示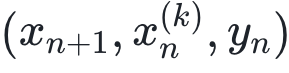 的联合概率分布。当我们去除用联合概率分布求期望的操作后,计算的便是局部转移熵了。下图展示的便是局部转移熵和局部活跃信息存储的区别。要注意,局部活跃信息存储作为一种互信息是没有方向的或者说是双向的,而局部转移熵是有方向的。
的联合概率分布。当我们去除用联合概率分布求期望的操作后,计算的便是局部转移熵了。下图展示的便是局部转移熵和局部活跃信息存储的区别。要注意,局部活跃信息存储作为一种互信息是没有方向的或者说是双向的,而局部转移熵是有方向的。
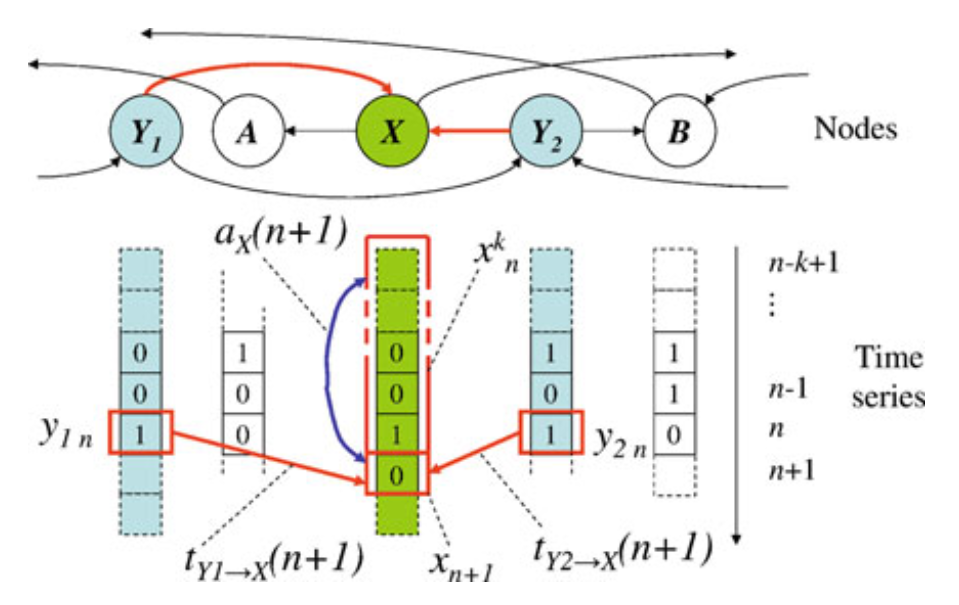
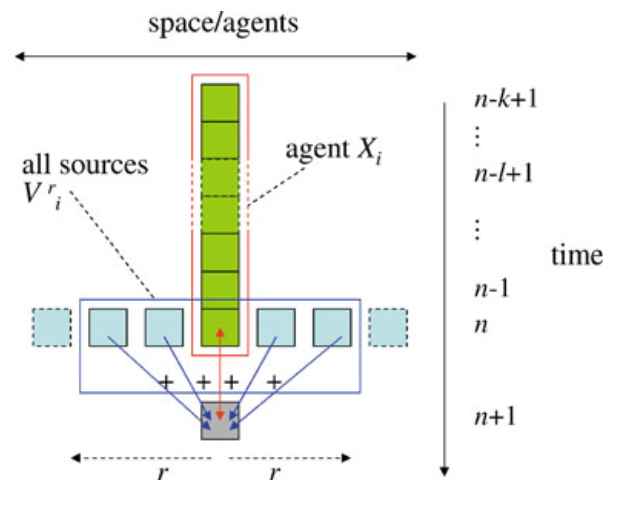
此时我只考虑了某一个源对目标的影响,但系统本身的情况可能更为复杂,不同几个源之间会存在相互作用。于是我们进一步可以对转移熵进行分类,如下图所示,如果我们只考虑某一个源主体转移的信息(如上面公式所描述的那样),那么它被称为表面转移熵(apparent transfer entropy)。而如果我们想度量只来自于某一个源,同时不来自于目标主体自身的历史,也不来自于其他潜在的源主体的那部分信息时,我们要计算的指标叫做完全转移熵(complete transfer entropy),如下图(b)所示。
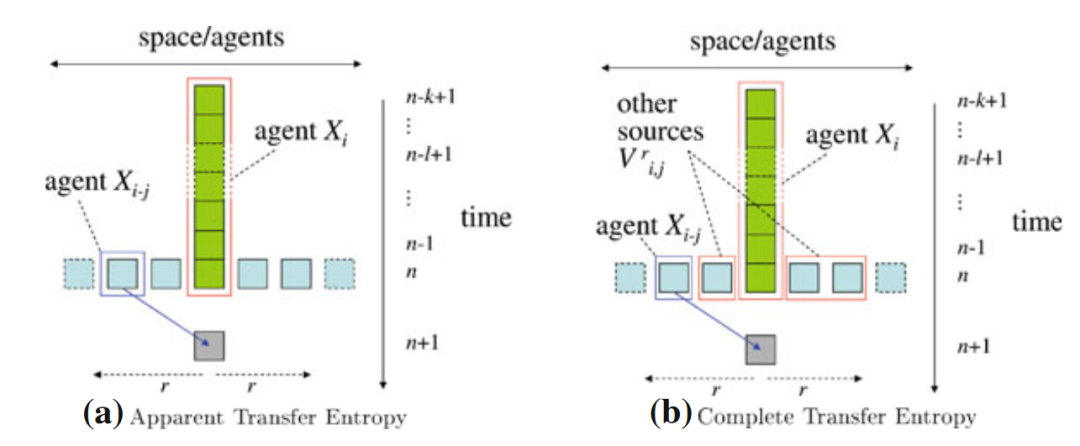
图(b)中 表示的便是,在目标主体一定范围大小(r)的领域内除了目标主体和某一个源主体以外其他潜在的源主体。在计算中,我们会把其他潜在源主体放到条件互信息中条件的位置上。下面就是局部完全转移熵的表达式:
表示的便是,在目标主体一定范围大小(r)的领域内除了目标主体和某一个源主体以外其他潜在的源主体。在计算中,我们会把其他潜在源主体放到条件互信息中条件的位置上。下面就是局部完全转移熵的表达式:
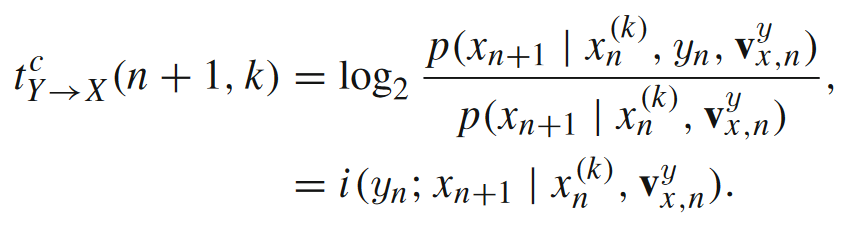
如果我们把所有可以作为源的主体都考虑进来计算转移熵呢?这个指标当然也有对应的意义,可以被称为集体转移熵(collective transfer entropy)。有意思的是,如果在一个完全确定的系统中(比如初等元胞自动机),集体转移熵就等价于熵率。这个等价关系所反映的事实是,除去一个细胞的历史信息以外,该细胞下一时刻状态的剩余不确定性就来自于其他细胞对它的相互作用。要注意,集体转移熵并不简单等于所有源的表面或完全转移熵之和,正如联合互信息不等于互信息之和一样。这暗示了我们需要信息分解框架来解释它们之间的关系,读者可参阅《从分解到整合:整合信息分解框架》。
接下来我们回到元胞自动机的案例,看看信息转移如何在元胞自动机中被度量。
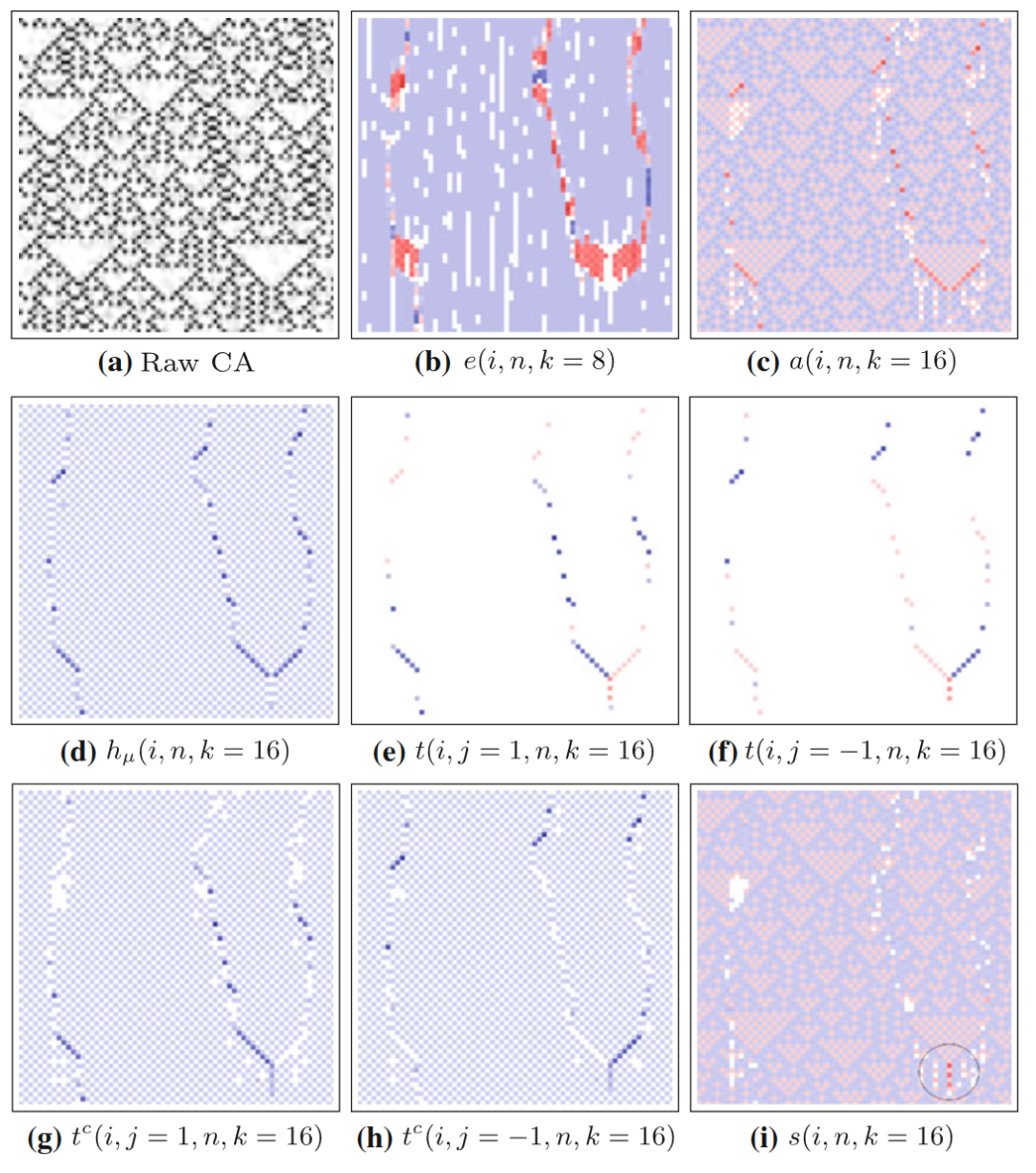
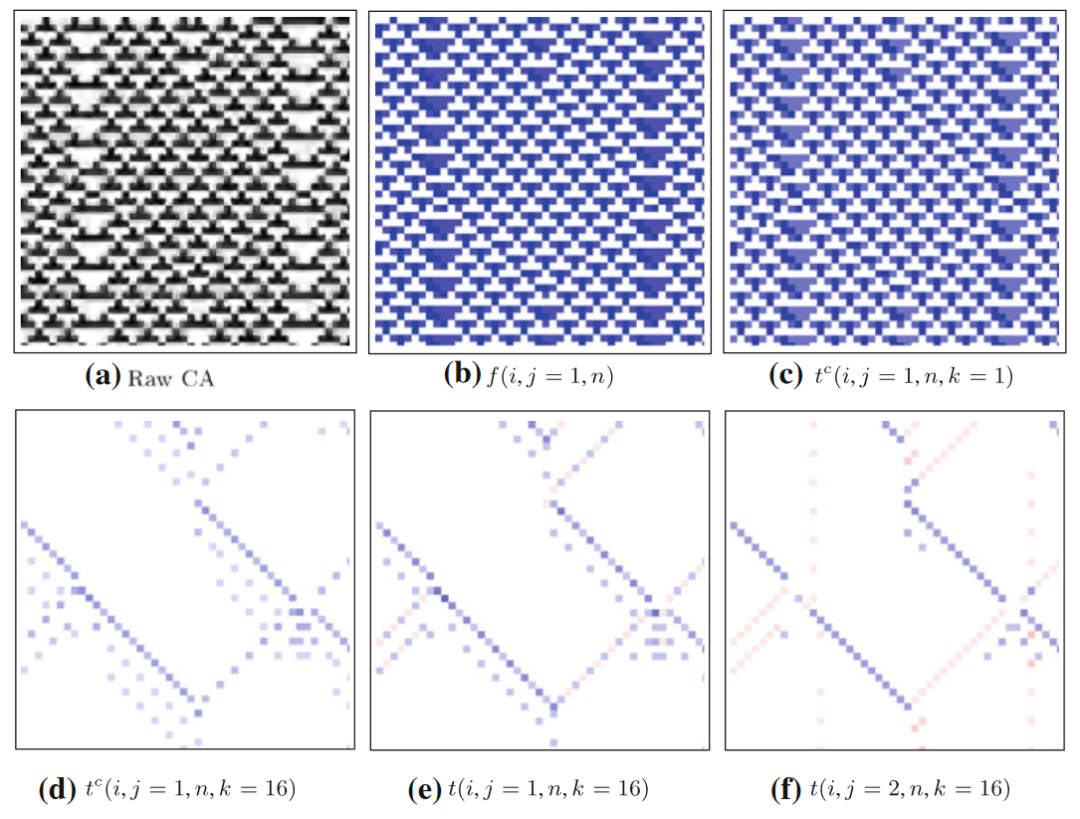
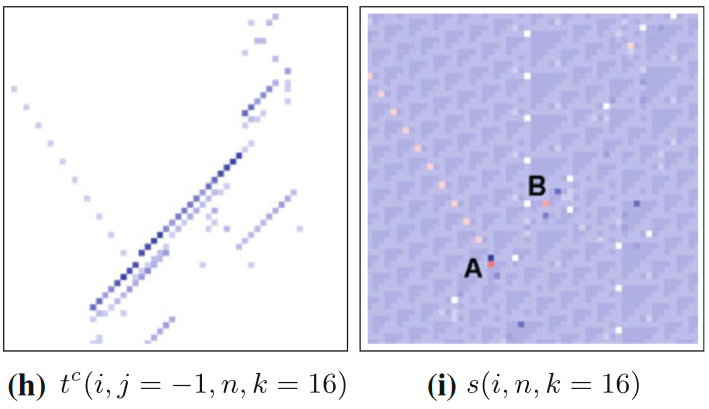
图中所展示的是18号规则元胞自动机和各种指标的分布图,67个细胞的67个时间步。图(d-h)展示的就是各种局部转移熵(如前文所述,局部熵率就是局部集体转移熵,tc表示局部完全转移熵,没有上标的t表示局部表面转移熵),其中j=1和-1分别表示源主体在目标主体的左侧和右侧;图(i)与信息修正有关,会在后面的章节中讨论。可以看到,相比于局部活跃信息存储等指标,局部转移熵能更清晰地捕捉运动粒子。事实上,对于一个运动粒子来说,局部转移熵更倾向于标记它在时间轴上最前沿的边界,因为只有在这里主要发生信息转移,而在粒子的其他区域则主要发生信息存储。
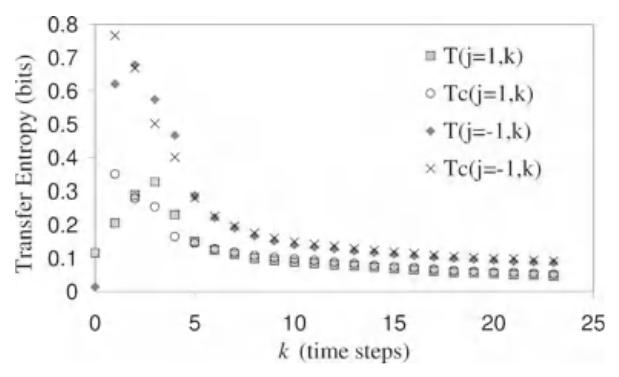
前文讨论过,历史长度k的选取对结果非常重要,在转移熵这里也是如此,它关乎到有没有去除信息存储的部分。当k较小时,转移熵中有一部分信息是目标主体的历史所提供,所以为了捕捉到纯粹的信息转移,k的取值越大越好。下图是随着k的增大,各种转移熵的变化曲线。
另外从18号规则元胞自动机的转移熵分布图中也能发现,对于域,也有微弱的信息转移。有时候会因为k不够大而出现虚假的信息转移,但这里不是这种情况。这种微弱的信息转移是一种环境转移(ambient transfer),捕捉的是滑行体的缺席。滑行体作为一种粒子,标志着一个域的边界,而没有滑行体出现,其实就是在告诉细胞要继续维持这个域,而这也是一种信息,只不过相比于滑行体的出现而言信息转移的值不高。为什么局部表面转移熵分布图(18号元胞自动机图(e)(f))里没有体现这一点呢?在18号规则元胞自动机里,域里的信息转移实则是一个异或门过程:一个目标主体的状态是由多个源XOR运算得到的,当有某一个源未知时,其他源对目标的信息转移都是0(局部表面转移熵为0),而当其他源状态已知时,剩余的源可以完全确定目标主体下一时刻状态(局部完全转移熵和局部熵率都为1bit)。
但这也不意味着局部表面转移熵就没有额外的作用了。对比表面转移熵和完全转移熵,我们会发现局部表面转移熵会出现负值,而这与方向有关。对比18号元胞自动机的图(e)与(f),两个方向的局部表面转移熵有一种互补的关系,其中一个为正值时另一个为负值。因为选错了源主体,转移的信息反倒会起误导的作用。而局部完全转移熵因为考虑了一定范围内所有的源,所以某一个源最差也是没有提供任何信息,而不会误导观察者。
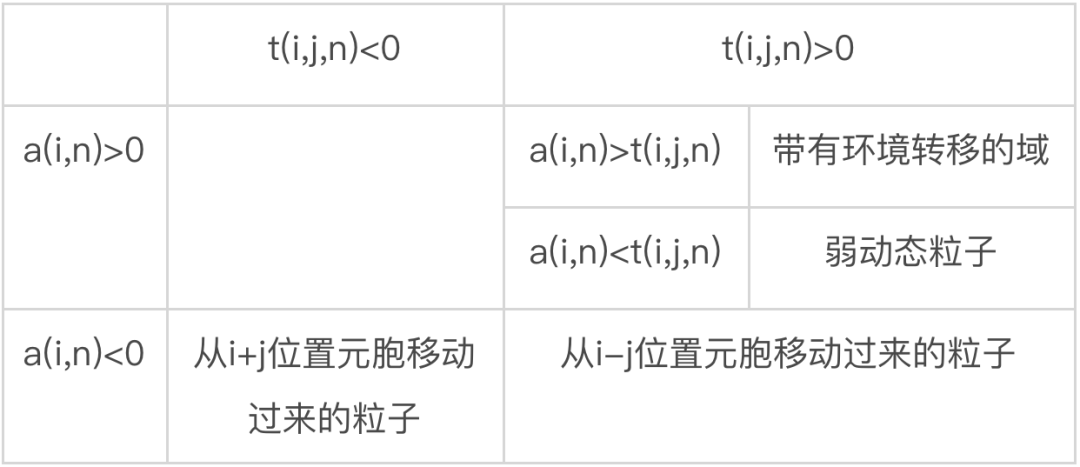
信息转移多微弱才算是环境转移呢?这其实需要和局部活跃信息存储a(i,n)做对比。因为环境转移发生在域上,所以此时a(i,n)仍是正值,即元胞没有被转移来的信息所误导。如果局部表面转移熵t(i,j,n)<a(i,n),那么这就是微弱的环境转移,而如果t(i,j,n)>a(i,n), 那么这可以被看做是一个弱动态粒子(原文称作“滑行体的尾迹”,the “wake” of a glider)。它也算是一种滑行体, 只不过比较弱小,不足以打破域的持续。
关于转移熵的应用中,有一个非常著名的概念——格兰杰因果。但是,转移熵是否真正刻画了因果关系?我们都知道相关非因果,因果关系的刻画应当不只依赖于时间先后的区别。Pearl 为了定量化因果关系,提出了干预(intervention)这一概念[5]。它本质上是在问这样一个问题:如果我改变了源的状态,目标的状态会在多大程度上发生改变?沿着Pearl的框架继续发展,Ay和Polani提出了信息流(information flow)这一指标,旨在捕获转移熵捕获不到的因果效应[6]。我们直接来看局部信息流的表达式。
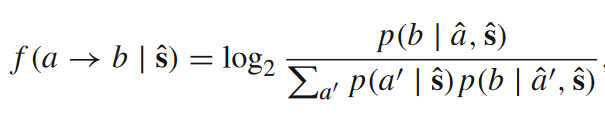
公式里出现了一个新的概念,在干预发生后的条件概率(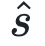 表示对s进行了干预)。通过下面的式子我们来看这样的干预是如何计算的。
表示对s进行了干预)。通过下面的式子我们来看这样的干预是如何计算的。
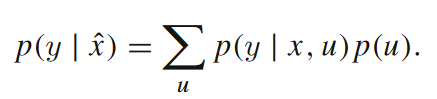
可以看到,为了计算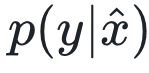 ,我们需要引入变量u。u指的是所有会对x产生影响的变量,而通过求期望的操作,相当于在因果图中消除了所有指向x的因果箭头,从而完成对x的干预。跟因果图相关的概念,读者可以参考文章《因果图的概念及其应用》。通过下面这张图,我们再来体会一下元胞自动机中如何计算干预后的条件概率。
,我们需要引入变量u。u指的是所有会对x产生影响的变量,而通过求期望的操作,相当于在因果图中消除了所有指向x的因果箭头,从而完成对x的干预。跟因果图相关的概念,读者可以参考文章《因果图的概念及其应用》。通过下面这张图,我们再来体会一下元胞自动机中如何计算干预后的条件概率。
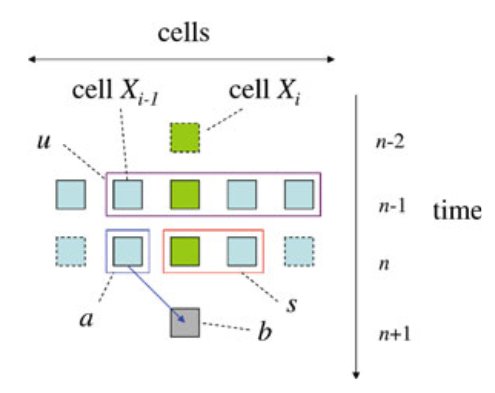
如图所示,源主体是Xi-1,目标主体是Xi,我们想要计算的局部信息流是从a到b的。当“环境”s需要被干预时(s指的是除了a以外能够影响b的变量),我们要引入的变量u,就是n-1时刻那四个能够影响s的变量了。当然,在干预a时,我们还要把变量Xi-2,n-1考虑进来,因为它能够影响a。
那局部信息流这个指标在元胞自动机上的使用效果如何呢?下图是45个细胞大小的54号元胞自动机,对比图(b)与(c)不难看出,局部信息流与k=1时的局部完全转移熵作用是相当的(在因果结构非常清晰的元胞自动机上是如此,换一个系统不一定满足等价关系),捕捉的是所有的直接因果效应。在域上因果效应普遍存在,而这一点在考虑相当长历史信息的局部转移熵中都丢失了。与此同时,原本局部转移熵能够识别的涌现的斑图则没有被局部信息流识别出来,因为更长周期的变化往往被储存起来,直至若干步后再提取。局部信息流指标没有考虑更长的历史,自然无法识别出更长周期的斑图。
至此,我们展示了所有和信息转移相关的计算指标,如下表所示。

关于元胞自动机涌现结构的识别,我们可以从信息转移的角度总结出以下判断准则:
3. 信息修正
前面的讨论其实一直没有涉及一种情况,如果两个粒子相撞怎么办?这实际上关乎第三种信息动力学,信息修正(information modification)。信息修正可以被解释为从不同源传递来的信息的交互,无论传递来的信息是一种信息存储还是信息转移,而这种交互导致了修正现象的发生。我们来看元胞自动机里两个滑行体相撞的情形。
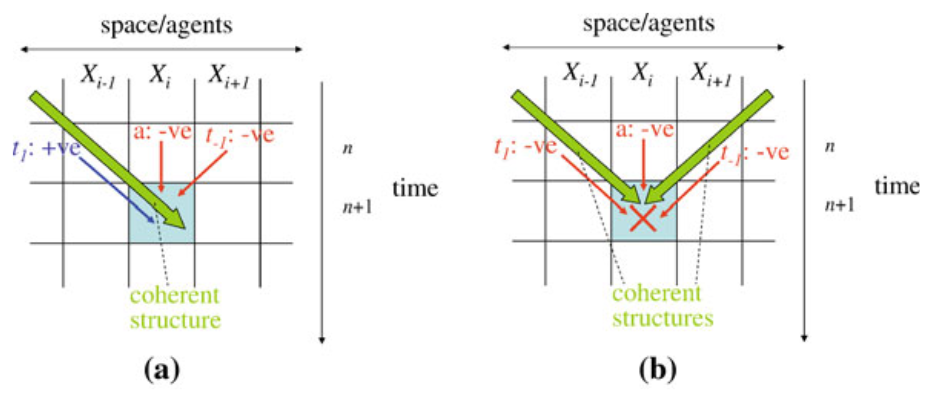
上图(a)展示了一个滑行体从左上角而来,属于一种典型的信息转移行为。其中唯有正确方向的转移熵计算出来的正值,而局部活跃信息存储和另一个方向的局部转移熵都是负值。当然,这似乎就已经满足了我们对信息修正的定义,而图(a)中的情形确实可以发生一种软碰撞(soft collision)。而与软碰撞相对应的,就是硬碰撞(hard collision),即图(b)中的情形,在后文中将更加细致讨论这两种碰撞。当两个滑行体相遇时,任何一个滑行体都没办法按照自己固有的规律来准确预测下一时刻元胞的状态,所以局部转移熵都是负值。对于恰好处于碰撞点的元胞来说,更是无法预料两个滑行体的碰撞会给自己的“命运”带来何种变化,所以局部活跃信息存储也是负值。
那我们可以用什么指标来识别这种不平凡的信息修正呢?本文作者Lizier提出可分离信息(separable information)来解决这一问题[7]。老样子,我们直接来看它的局部表达形式。
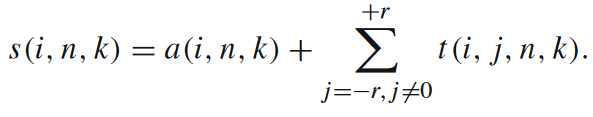
如果你已理解了信息存储和信息转移的数学语言,那不难看出局部可分离信息就是把局部活跃信息存储和一定领域内所有源的各自的局部表面转移熵加在一起,下图是对该指标的一个图解。虽然它数学表达式比较简单,但我们需要进一步想清楚它的物理含义。可分离信息实际代表的是,在对某一个元胞下一时刻做预测时,我们能否对所有源进行分别单独地观测。如果s(i,n,k)是负值,就意味着所有源单独对目标提供的信息加在一起都不足以让观察者对目标做出正确的预测,要想准确预测目标主体下一时刻状态,我们必须要把所有的源作为一个整体来观测,即考虑到源与源之间的交互作用。
我们回过头来看18号元胞自动机中应用可分离信息指标的效果,如下图所示。圆圈所标记的三个大红点便是发生两个滑行体硬碰撞的地方,可见局部可分离信息可以清晰地在发生硬碰撞的地方显现出负值。三个红点的上方存在两个滑行体相向而行,可由局部转移熵识别出来。
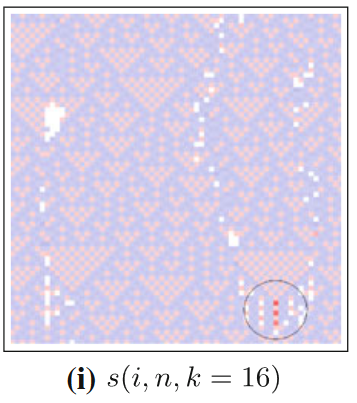
上面展示的便是典型的硬碰撞,而前文已经提及过,即使是只有一个滑行体,也可能出现微弱的信息修正,即软碰撞。比如在110号元胞自动机中,我们可以看到这样的现象。下图(i)中A点处有深红色点,代表着两个滑行体的硬碰撞,而在A点的左上方,有一列浅红色点。这些点在图(h)中可以由局部完全转移熵识别出来,是滑行体的轨迹。作者认为这是一个滑行体与域中的环境转移相遇时的软碰撞,也可以被局部可分离信息识别出来。
每次碰撞发生,都好像是在运行一个函数。这个函数的两个输入是将要发生碰撞的两个信息载体。那输出结果,显然不只是跟输入有关,还跟这个函数本身的性质有关。我们不妨设想这样一个函数f,不管输入是什么,输出都是f(x)=0(这个函数也有一个名字“reset to zero”,RTZ)。从信息的角度来看,这里有一个显然的事情发生了——有信息被损毁了。我们无法从它的输出0,推断出原本的输入是什么样子的。损毁,或者说擦除,意味着该信息将无法再恢复。著名的兰道尔原理建立起了信息和物理学中能量这一概念的联系。其中提出,每擦除 1bit 信息,需要消耗 kTln2 焦耳的能量。那这样的信息损毁,在分布式计算中扮演着什么角色呢?它和前面提到过的信息修正又有什么关联呢?
为了刻画这种不可逆的信息损毁,我们引入本文最后一个定量指标,其名称就叫做信息损毁(information destruction)。跳过冗余的数学细节,我们直接来看它在元胞自动机里的局部表达形式。
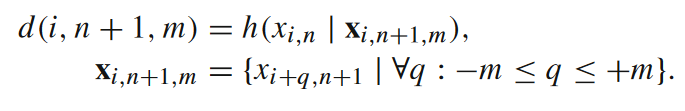
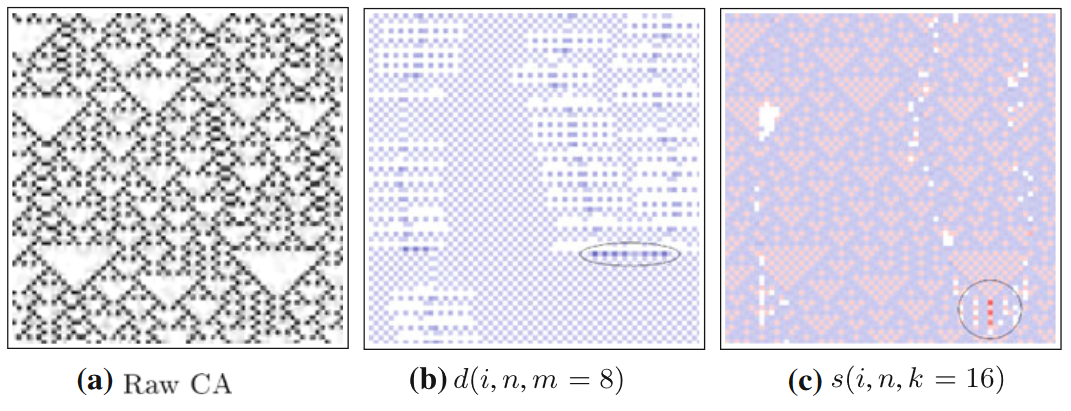
读者可参考下面对该公式的图解。局部信息损毁实际上就是在算一种局部条件熵,但和前面提到过的熵率很不一样,它是在已知n+1时刻某些元胞状态的条件下,求对n时刻某一个元胞状态的条件熵。也就是在问,当我们已知未来时,对当下状态的预测还剩余多少不确定性。这个值越大,说明信息损毁的程度越高。在RTZ的例子中,因为我们无法从输出反推出关于输入的任何信息,所以信息损毁的大小就是输入变量的熵(或事件的局部熵),即全部信息都被损毁了。
回到元胞自动机的例子,如下图所示。对比图(b)和图(c),我们发现局部信息损毁发生在信息修正的若干步之前(图中两个黑色椭圆的标记)。所以信息损毁的出现可以作为粒子碰撞将要发生的预警。此外,我们能看到域中有微弱的信息损毁广泛存在。如前文“信息转移”章节中所述,18号规则元胞自动机在域里有异或运算。异或运算的反推可以让我们知道两个输入之间的关系,但无法获知其中任意一个输入的具体状态,所以有信息损毁。
下面我们列出这一章节所提及的指标和它们的作用。

d(i,n+1,m)<0
发生信息损毁
s(n,k)<0
绝对值较小时,软碰撞
绝对值较大时,硬碰撞
4. 结语
至此,我们已经介绍了一整套的定量框架,能够刻画和阐释元胞自动机里发生的涌现结构和分布式计算。如果你不想细究抽象的数学符号和繁杂的运算细节,可以着重体会以下更为粗糙的总结:在元胞自动机里,静态的粒子(闪烁体)进行着信息存储,动态的粒子(滑行体)进行着信息转移,而粒子的碰撞则是在进行信息修正。在更为复杂的元胞自动机上(比如生命游戏),这种涌现出来的粒子甚至可以作为基本的运算单位,用来构建图灵机,模拟任意复杂的其他的计算过程。
初等元胞自动机是非常合适的实验对象,可以帮助我们理解这诸多指标的含义和区别。在元胞自动机之后,我们在下一篇文章看一看,这些定量指标在更为广泛的物理、生物等系统中有哪些实际应用。
参考文献
[1] J. Dasan, T.R. Ramamohan, A. Singh, P.R. Nott, Stress fluctuations in sheared Stokesian suspensions. Phys. Rev. E 66(2), 021409 (2002)
[2] J.E. Hanson, J.P. Crutchfield, The attractor-basin portait of a cellular automaton. J. Stat. Phys. 66, 1415–1462 (1992)
[3] M. Mitchell, J.P. Crutchfield, P.T. Hraber, Evolving cellular automata to perform computations: mechanisms and impediments. Physica D 75, 361–391 (1994)
[4] T. Schreiber, Measuring information transfer. Phys. Rev. Lett. 85(2), 461–464 (2000)
[5] J. Pearl, Causality: Models, Reasoning, and Inference (Cambridge University Press, Cambridge, 2000)
[6] N. Ay, D. Polani, Information flows in causal networks. Adv. Complex Syst. 11(1), 17–41 (2008)
[7] J.T. Lizier, M. Prokopenko, A.Y. Zomaya, Detecting non-trivial computation in complex dynamics, ed. by F. Almeida e Costa, L.M. Rocha, E. Costa, I. Harvey, A. Coutinho, in Proceedings of the 9th European Conference on Artificial Life (ECAL), Lisbon, Portugal, ser. Lecture Notes in Artificial Intelligence, vol. 4648. (Springer, Berlin/Heidelberg, 2007), pp. 895–904
Joseph T. Lizier 的工作在 CORE 博士论文奖中获得了荣誉提名,并被 Springer Theses 收录。该系列论文精选世界各地在相关领域具有重要影响的博士论文,并包含博士生导师对该研究在相关领域影响的介绍,因而对非专业的跨领域读者也具有较高的可读性。这篇论文的目录如下:
1.引言
2.复杂系统中的计算
3.信息存储
4.信息转移
5.信息修正
6.网络和相变中的信息动力学
7.复杂计算中的连贯信息结构
8.生物系统中的信息转移
9.总结
我们计划将其分为三大部分介绍,第一篇文章《复杂系统研究为什么关注信息论?》主要解读前两章,聚焦问题背景以及复杂系统和信息论的结合;第二篇文章解读三到五章,这是论文最核心的概念框架;最后一篇解读六到九章,进一步探讨具体的应用价值。欢迎感兴趣的读者持续关注,我们下一篇见!
作者简介

杨明哲,北京师范大学系统科学学院硕士生,张江老师因果涌现研究小组成员。研究领域是因果涌现、复杂系统自动建模。
学者主页:https://pattern.swarma.org/user/76769
新信息论:从分解到整合
因果涌现读书会第四季
什么是意识?意识能否度量?机器能否产生意识?对于意识问题,人们可能即将迎来一个大的突破,各种有关意识的理论正如雨后春笋般展现出勃勃生机。其中神经科学家 Giulio Tononi 的整合信息论(IIT)被认为是最有前景的意识理论之一。如果说意识是大脑神经活动的一种涌现结果,那么刻画涌现便成为理解意识过程中一个重要环节。因果涌现理论目前发展出两个派别,除了 Erik Hoel 的有效信息因果涌现框架,还有一个是 Rosas 的信息分解(PID)框架,此后 Rosas 基于此进一步提出融合整合信息论的信息分解框架 ΦID,尝试构建新的意识理论。
一边是信息整合(IIT),一边是信息分解(PID),看似分裂,实际上都是对香农经典信息论的进一步发展。因果涌现读书会第四季「新信息论:从分解到整合」由北京师范大学系统科学学院教授、集智俱乐部创始人张江老师领衔发起,旨在梳理信息论领域的发展脉络,从香农的经典信息论开始,重点关注整合信息论和信息分解这两个前沿话题,及其在交叉领域的应用。希望通过对这些“新信息论”度量指标的深入探讨,帮助我们理解什么是意识,什么是涌现,并找到不同学科,不同问题背后的统一性原理。
推荐阅读
1. 复杂系统研究为什么关注信息论?2. 计算力学:量化涌现的又一条路径 3. 从分解到整合:整合信息分解框架4. 张江:第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 龙年大运起,学习正当时!解锁集智全站内容,开启新年学习计划6. 加入集智,一起复杂!
点击“阅读原文”,报名读书会




 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


