斯坦福华人博士生打破58年僵局！牛顿提出的亲吻数问题有了新突破

一水
2025-02-09
12:07:03

来源：量子位

牛顿想出的“球体亲吻数”（kissing number）难题，华人学者取得新进展。

n维空间中，给定一个n维球体，最多有几个相同的球体可以与它接触而不重叠？

斯坦福博士生Anqi Li在微软实习期间完成这项研究，导师Henry Cohn本意是让她用计算机辅助，她却创造性地找到了数学上的新解法。

这个问题在低维很直观，比如二维空间的“亲吻数”是6，如果在桌面上摆一枚硬币，很快就能试出来周围最多还能摆6枚硬币。

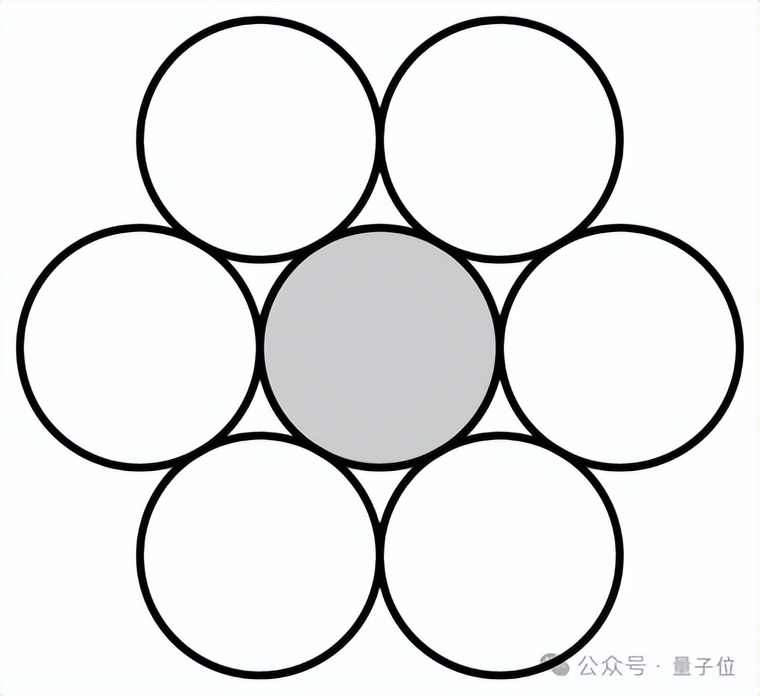
在三维空间，“亲吻数”是12。

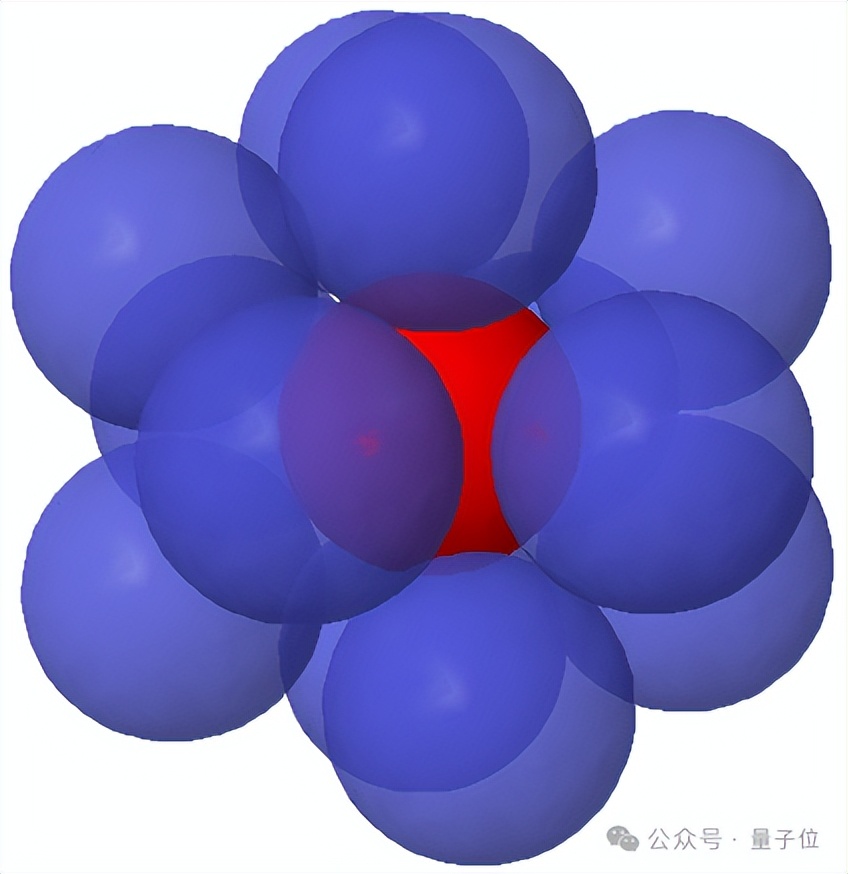
到了更高维空间就无法直观的可视化，解决起来也更困难，但几个世纪以来科学家一直在努力研究。

另外，这个问题还与通信领域的编码纠错问题密切相关，曾被NASA用来设计旅行者号探测器的通信编码：

使用24位二进制编码，仅需一个灯泡的功率（约20瓦），就将彩色照片从太空传回地球。

那么，二进制编码与高维球体是怎么联系起来的？

如果将每个通信编码看做高维空间中的一个点，这个点也可以被视为一个球体的球心。

此时球的半径就代表了容错的范围，当传输过程中出现噪声导致信息失真时，接收到的信息会偏离原始编码。

但如果失真后的信息仍落在某个编码词对应球体的范围内，就可以识别出原本要传输的编码，这就实现了通信中的错误纠正。

至此，通信编码设计问题就转换成了求解高维空间中球体堆砌问题，而亲吻数问题正是研究局部最优堆砌的重要工具。

反过来也成立，编码设计的进步也能帮助数学家改进高维亲吻数问题的结果。

球体亲吻问题

时间倒回到1694年5月，当时在剑桥大学校园内，两位顶尖科学家艾萨克·牛顿（Isaac Newton）和大卫·格雷戈里（David Gregory）进行了一次关于恒星本质的著名讨论。

这场讨论最终诞生了经典的球体亲吻数问题：

给定一个中心球体，可以排列多少个相同的球体，使得它们互相接触但不重叠？

对于三维空间，牛顿认为这个数是12，格雷戈里认为是13。

直到1952年，数学家才证明牛顿是对的。不过观察三维空间的最优解，就很容易理解格雷戈里为什么猜测还能多容纳下一个球。

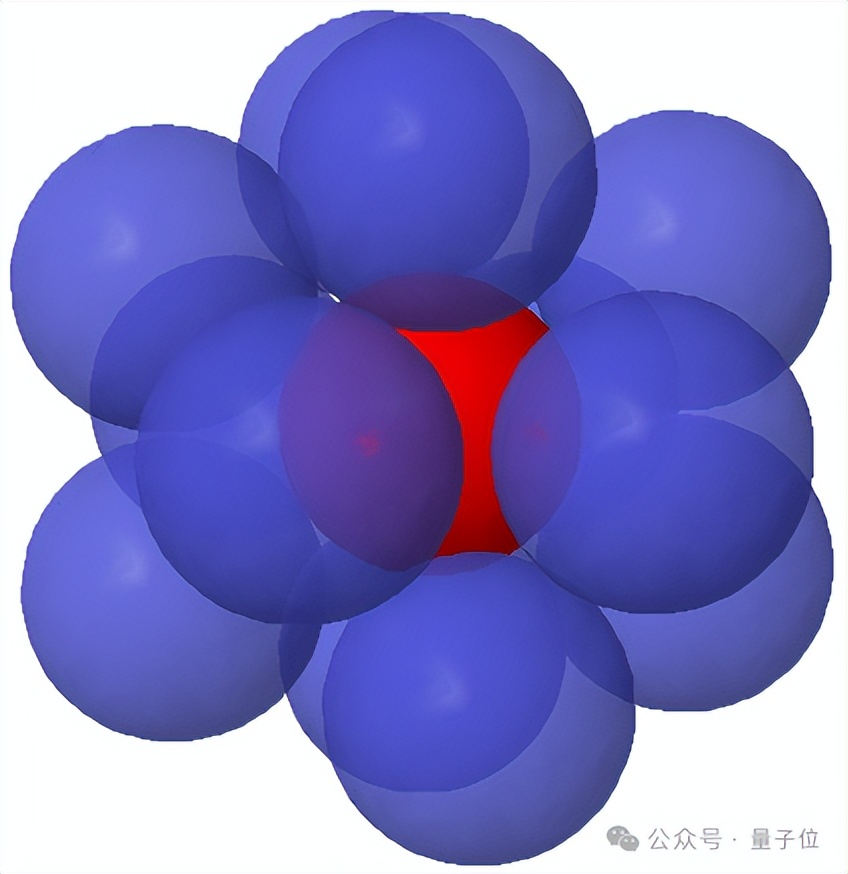
总的来说一个规律是，随着维度增大，球与球之间的空隙也在增加，问题也就越困难。

但这个规律却在24维的时候出现了例外。

1967年，数学家约翰·利奇 (John Leech) 构建了以他的名字命名的利奇格（Leech lattice）。

使用这种晶格可以“完美”地将球体密集地填充到24维空间中，且该空间中的最佳的亲吻排列是每个球体接触196560个相邻球体。

但对于其他维度，尤其是几何上不那么对称的维度，亲吻数问题仍然难以解决。

长久以来，只能通过计算来估计高维空间亲吻数的上界和下界。

Anqi Li在刚开始接触这项工作时，导师Cohn对她的建议也是如此，像其他学生一样，用计算机辅助手段取得一些进展就好了。

Anqi Li本科毕业于MIT，硕士毕业于剑桥大学，目前斯坦福博士在读，除了Cohn外还接受过华人数学家赵宇飞等众多名师指导。

当她开始尝试“手动”方案的时候，Cohn还承诺她“即使没有任何结果仍然可以得到A的成绩。”

但不久以后，Cohn就发现她的进展“非常令人兴奋”。

时隔58年的新突破

Anqi Li首先研究了16维空间，已知最好的排列方式来自另一种“Barnes-Wall格”，可以被视为利奇格的一个切片。

Barnes-Wall格有一个特点，其中最常见的点，坐标中负号的个数总是偶数。

这有助于确保点与点之间的距离足够远，形成一个高度对称的结构。

Anqi Li的突破点在于“如果使用奇数个负号会如何？”，这需要额外的小心不要导致球体重叠，而且据她所知，以前还没人如此尝试过。

Cohn起初对这个方法抱有怀疑态度，但在使用计算机验证之后，发现球体的排列没有问题。

那年夏天，Anqi Li跟随Cohn去微软研究院实习，两人仔细改进了他们使用的编码方案，终于让17维空间的亲吻数下界从5346提高到了5730，相当于在空隙中多塞了384个球。

接下来，他们将类似的技巧推广到18维至21维，刷新了这些维度的亲吻数下界。

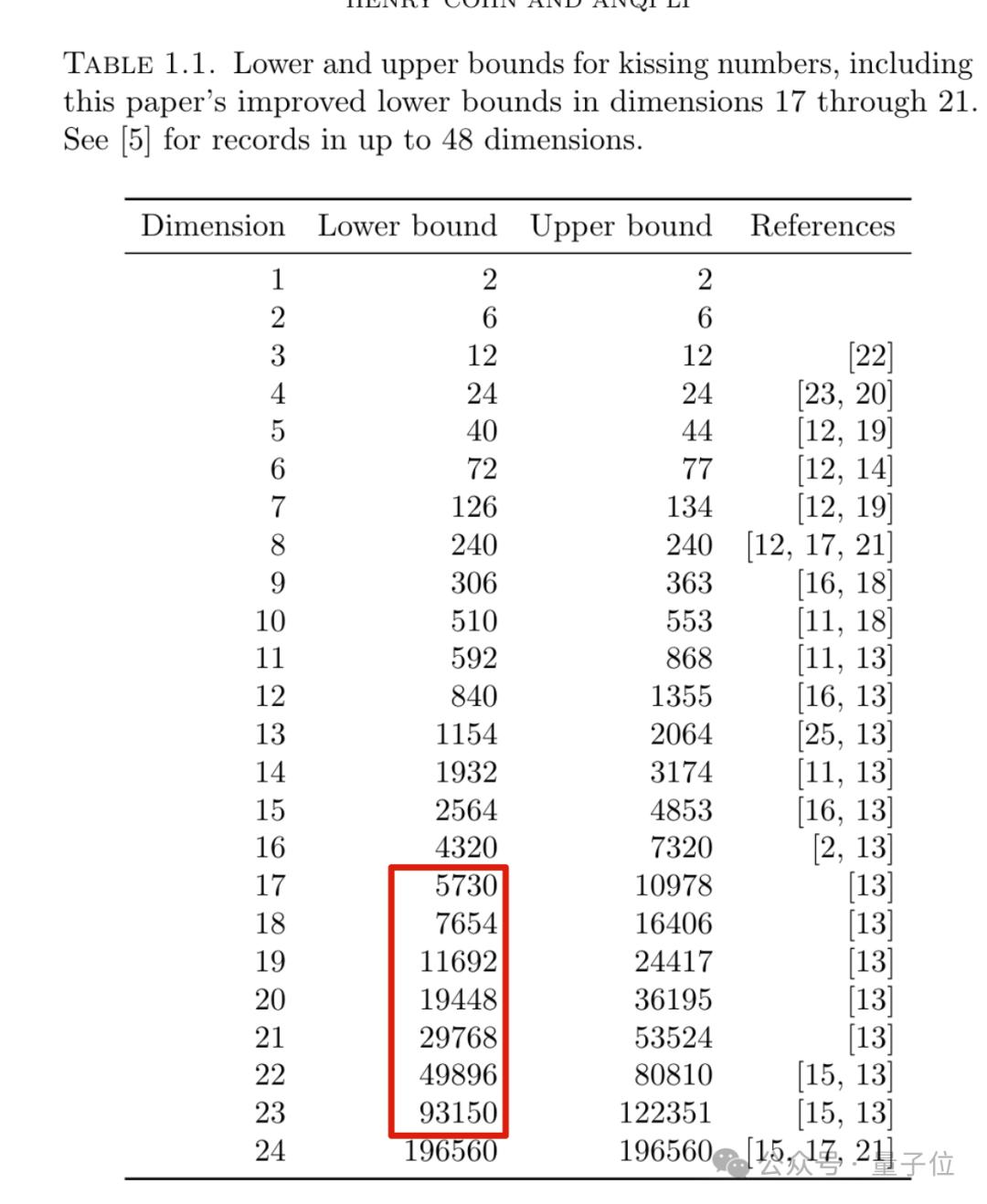
当然，他们的新纪录离最终答案可能还有一定距离。以17维为例，目前的上界估计高达10978就被认为是严重高估，表明还有不小的优化空间。

不过这种独辟蹊径的思路，也为后续研究指明了新的方向。

正如这个领域的另一位专家Oleg Musin（证明了4维空间中的最佳亲吻数）所评价的：他们提出了一种完全不同的构造方法。

虽然在24维已经有了利奇格这个“完美”解，但也给数学界带来一个更深刻的问题：为什么24维会存在如此优雅的解？

相邻维度的研究进展，也有助于帮助数学家们理解自然界这种优雅背后的深层机制。

论文地址：https://www.arxiv.org/pdf/2411.04916

Read More