陶哲轩亲测点赞o3-mini：专家级证明，我收到了一个完美的答案

十三
2025-03-11
14:12:46

来源：量子位

金磊 发自 凹非寺

量子位 | 公众号 QbitAI

刚刚，陶哲轩亲测了一下o3-mini，然后他给出了这样的结论：

重建图论中一个标准（专家级）结果的证明，o3-mini是完全可以hold住的。

陶哲轩要重建的这个证明，叫做三角形移除引理（triangle removal lemma），由Ruzsa和Szemeredi于1978年提出，是极值图论中的重要结果:

对于任意的η＞0，都存在c>0，使得对于任意一个足够大的有n个顶点的图，如果该图中最多包含cn3个三角形，那么可以通过移除最多ηn2条边，使这个图变为无三角形的图。

用另一种表述方式就是，如果一个有n个顶点的图包含o(n3)个三角形，那么可以通过移除o(n2)条边来删除所有的三角形。

然后陶哲轩看罢o3-mini的作答后表示：

在几秒钟后，我收到了一个完美的答案，（o3-mini）正确地解释了这种蕴含关系。

o3-mini是如何作答的？

首先，我们来看下陶哲轩的Prompt：

Ruzsa和Szemeredi的三角形移除引理断言，如果一个具有n个顶点的图（n很大）包含o(n3)个三角形，那么可以通过移除o(n2)条边使其变为无三角形图。显然，这一引理蕴含了以下结论：如果一个具有n个顶点的图是n个诱导匹配的并集，那么它只包含o(n2)条边。你知道后者是如何从前者的结论中推导出来的吗？

对于这个问题，o3-mini的回答是这样的：

（注：为完整体现内容，o3-mini的作答将以英文呈现）

可以看到，o3-mini回答的逻辑还是比较清晰的。

一步一步展开论证，从起始条件（诱导匹配的并集），到构建辅助图，再到建立边与三角形数量的联系、应用引理，最后得出结论。

紧接着，陶哲轩开始追问了：

谢谢！三角形移除引理的另一个标准推论是(6,3)定理：如果一个具有n个顶点的3-一致超图不包含(6,3)-配置，即不存在六个顶点确定至少三个超边的情况，那么该超图只包含o(n2)条超边。你能解释一下为什么这也是三角形移除引理的一个推论吗？

o3-mini在思考了片刻后，开始作答：

o3-mini对这个问题的总结是：

在一个不包含任何 “(6,3)-configuration”（即任意六个顶点不生成三条或更多超边 ）的3-uniform 超图中，由于将超边编码为辅助图中的三角形后，辅助图的三角形结构受超图条件限制呈现 “稀疏” 状态 ，根据三角形移除引理可以推断出，该超图中的超边总数为o(n2)，也就是说这样的超图不会过于稠密。

在此之后，陶哲轩便开始加大难度：

感谢你的大致概述！我有兴趣将其扩展成一个更详细的证明。我听说首先考虑超图是线性的情况会很有帮助——即任意两条超边不会共享两个顶点。你能将你的概述扩展成一个更精确的论证，专门针对线性情况吗？

这一次，o3-mini思考的时间足足是上个问题的四倍：

这次o3-mini的推理过程，是通过构造一个辅助图G，将超图中的每个超边对应到辅助图中的一个三角形。利用线性性质保证这些三角形边不相交，再通过假设m=Ω(n2)推出与三角形移除引理相矛盾的结果，从而证明原假设错误，得出超边数量的渐近上界 。

陶哲轩再追问：

如何确保图G不会产生任何额外的三角形，除了那些直接由超边生成的三角形之外？

至此，陶哲轩评价道：

好的，我认为这给出了(6,3)定理在线性情况下的完整证明。

然后继续追问o3-mini：

你有什么建议，如何建立一般情况下使用这个线性的情况？

o3-mini给出了一种“清理”的路数：

• 清理超图：通过删除少量超边使得到的子超图H’线性化，“(6,3) 条件” 保证不会移除过多超边。
• 应用线性情况结论：为线性超图H’构建辅助图，每个超边对应一个边不相交三角形。
• 利用三角形移除引理：过多的边不相交三角形会导致与引理矛盾，所以H’有o(n2)个超边。
• 推导原始超图的边界：因为H’保留了H’的几乎所有超边，所以原始超图H’也有o(n2)个超边。

陶哲轩认为这是一个不错的策略，并最后提出了一个问题：

你能不能试着给出一个更精确的清理步骤的描述，这个步骤可能会把一个一般的(6,3)超图转换成一个线性的(6,3)超图，并对边缘进行一些控制？

但也有局限性

在陶哲轩六连问之后，除了刚才提到的“完美答案”之外，他还给出了更加客观中立的评价：

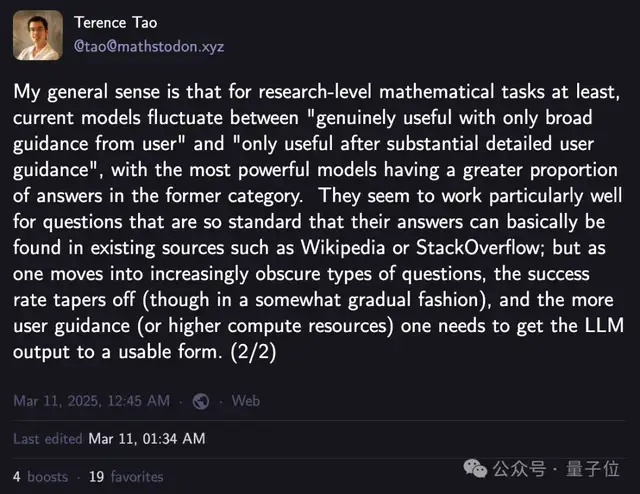
我的总体感觉是，至少对于研究级的数学任务，当前的模型在“仅需用户提供大致指导即可真正有用”和“只有在用户提供大量详细指导后才有用”之间波动，而最强大的模型在前者中的回答比例更高。

它们似乎特别适合那些非常标准的问题，这些问题的答案基本上可以在现有资源（如维基百科或StackOverflow）中找到。

但随着问题变得越来越冷门，成功率逐渐下降（尽管下降的方式较为平缓），并且需要更多的用户指导（或更高的计算资源）才能使LLM的输出达到可用的形式。

陶哲轩的这波实测也引发了不少网友的讨论。

例如有人质疑LLM的推理能力，认为它们是随机文本生成器，而不是真正的推理模型。他指出LLM的输出依赖于点赞/踩票信号，而不是真正的逻辑推理。

陶哲轩与o3-mini完整对话：
https://chatgpt.com/share/67cf13cf-53dc-800e-a382-e4ece8341a6d

参考链接：
https://mathstodon.xyz/@tao/114139145175476223

Read More