华人学者助力”数学大一统理论”新突破!4位数学家近10年完成证明
230页论文,朗兰兹纲领迎来新突破
明敏 闻乐 发自 凹非寺
量子位 | 公众号 QbitAI
4位数学家,耗时近10年,将“数学大一统理论”向前推动关键一步!
1994年,安德鲁·怀尔斯通过证明椭圆曲线与模形式之间的联系,解决了困扰数学界300多年的费马大定理。
时隔30年,4位数学家将这一关键理论从椭圆曲线扩展到了更复杂的数学对象。
这意味着,朗兰兹纲领取得了重大进展。

朗兰兹纲领被视为现代数学研究中最大的单项项目,被称为“数学大一统理论”,它提出数论、代数几何、群表示论这三个独立发展的数学分支之间其实密切相关。
诸多世界级数学家、菲尔兹奖获得者,都长期扑在这一领域的研究上。国内,“北大黄金一代”中恽之玮、张伟、袁新意、朱歆文也被该领域深深吸引。
此次最新成果,证明了普通阿贝尔曲面总能对应一个模形式。
4位数学家用230页论文,给出证明。
而值得一提的是,在这之中,出身北大数院的中国数学家潘略提出的相关研究,成为撬开这一突破的关键参考。
潘略本人,今年也刚刚获得素有“诺奖风向标”之称的斯隆奖。
将「模性」从椭圆曲线扩展到阿贝尔曲面
简单概括,此次最新突破在于,通过扩展模性理论,实现阿贝尔曲面与模形式的联系。
模形式是一种在数学里很特别的函数,它的“家”是复上半平面。
也就是所有虚部大于0的复数组成的区域。
简单来说,对于复上半平面的每一个点
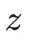
,模形式都能给出一个对应的函数
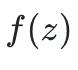
。
并且,用特殊整数矩阵(行列式为1的二阶整数矩阵)对点
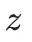
进行变换时,无论怎样变换,变换后的
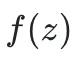
都和原来的函数值有一定的关系。
可以说这就是模形式最大的特点——对称性。
这种对称性让数学家们研究起来相对容易一些。
1994年,安德鲁・怀尔斯和理查德・泰勒在证明费马大定理时,建立起了模形式与椭圆曲线的联系——「模性」。
模性揭示了模形式与椭圆曲线就像是两个相互映照的世界。
数学家如果想探究椭圆曲线的某些性质,可以借助模形式,先在模形式的世界中找到对应的镜像进行研究,再将结论带回椭圆曲线领域。
朗兰兹纲领期望将这种联系拓展到更广泛的范畴。
历经10年时间,4位数学家将「模性」从椭圆曲线扩展到更复杂的阿贝尔曲面。
在椭圆曲线的变量

和
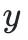
之外再添加一个变量
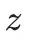
,就得到了一个三维空间中的弯曲曲面——阿贝尔曲面。
这种三维变量看起来似乎也应该有某种对应的模形式。
于是4位数学家于2016年开始合作,希望遵循泰勒和怀尔斯在椭圆曲线证明中所采取的步骤进行研究。
这时候,问题来了。
额外的变量使模形式构造起来非常困难。
对于给定的阿贝尔曲面,建立模形式的相关数很容易计算,但构造出来的模形式无法匹配每一个曲面。
于是,他们开始尝试反向建立——先构造一个模形式,它的相关数只要在“较弱”的意义上与普通阿贝尔曲面相匹配就足够了。
这种弱联系要求模形式的相关数只需要在时钟算术中等效。
在数学里,时钟算术是一种循环运算。
以我们平常使用的时钟为例,一圈是12个小时,假设现在是3点,再过5小时后,不是3+5=8点,而是3+5-12=8点,这里的12就称为“模”。

再比如,在“模7”的时钟运算中,3点再过5小时就是3+5-7=1点。
而团队期望的“弱联系”只需要在“模3”的时钟运算中将构建的模形式的相关数与普通阿贝尔曲面的相关数匹配,就能将两者联系起来。
然而构建满足该条件的模形式又是困难重重。
后来,他们又发现了一组按“模2”时钟运算易于计算的模形式,可阿贝尔曲面需要“模3”时钟运算的结果。
于是问题又来了。
如何在两种不同时钟运算间建立紧密的联系?
这个难题在2023年终于有了突破。
其中关键,来自中国数学家潘略之前发表的一篇论文。
潘略在2020年发布了一个模形式的证明,与四人组要论证的问题意外相关。
这项研究揭示了局部解析向量与模形式和伪同调之间的关系,为研究模形式提供了新的工具。
具体来说,潘略引入了一个微分算子(differential operator),并通过研究模曲线完备上同调中的局部解析向量,揭示了这些向量满足特定的解析性条件。
刚好4位科学家需要构造阿贝尔曲面对应的模形式,潘略提出的分析方法能有效处理模形式的局部结构。微分算子的技巧,为解决模形式的构造问题提供了新方向。
同时,潘略给出的关于超收敛模形式经典性的结果(即证明某些超收敛模形式实际上是经典模形式),这也为4位科学家提供了验证模形式联系的重要工具。

在2023年夏天,他们就通过线上会议,开始讨论如何改进潘略提出的方法。
比较有趣的是,当时团队为了不被外界打扰,做研究的场所选在了地下室。
整整一周时间,他们每天在地下室工作12个小时来研究潘式定理,只有在喝咖啡的时候,才来地面上透口气。
喝完咖啡后,数学家们还自己调侃:我们要回“矿井”了。
但也是经过这一周,数学家们差不多确定自己已经成功了。
潘略的研究成果给四人组提供了新的思路和方法,帮助团队跨越了从“模2”时钟运算的模形式到适用于普通阿贝尔曲面的“模3”时钟运算之间的关键障碍。
后面一年半时间里,他们将这些证明写成了一篇长达230页的论文,于2025年2月正式发布到arxiv上。
从影响上来看,这项新成果不仅开辟了研究阿贝尔曲面的新方向,还可能催生类似于椭圆曲线的“伯奇与斯温纳顿-戴尔猜想”(涉及阿贝尔曲面)的新数学猜想。
未来团队将与潘略继续合作
将近十年的成果刚刚发布不久,4位数学家已经在推进下一步探索了。
他们将和潘略合作,尝试将现在的成果扩展到非普通的阿贝尔曲面上。对于这项新计划,他们也很自信。
如果10年后,我们还没有找到几乎所有的可能,那我会很惊讶的。
本次新进展一共由4位数学家带来,他们分别是:
- 托比·吉(Toby Gee)
- 文森特·皮洛尼(Vincent Pilloni)
- 弗兰克·卡莱加里(Frank Calegari)
- 乔治·伯克森(George Boxer)。
托比·吉(Toby Gee)是一位英国数学家,主要研究数论和朗兰兹纲领。2024年当选为英国皇家学会会员。

文森特·皮洛尼(Vincent Pilloni)是一位法国数学家,主要研究算术几何和朗兰兹纲领。2021年获得费马奖。

弗兰克·卡莱加里(Frank Calegari)是芝加哥大学数学系教授,主要研究数论和朗兰兹纲领。曾先后获得1992年IMO铜牌、1993年IMO银牌。

乔治·伯克森(George Boxer)目前在伦敦帝国学院数学系,是英国皇家学会大学研究员。
以及对本项研究产生重要影响的华人学者潘略。
他今年刚刚获得了素有“诺奖风向标”之称的斯隆奖。

他2009年获得CMO银牌,从人大附中被保送至北京大学数学系(也就是常说的“北大数院”)。不过当年他还是参加了高考,数学成绩满分,是海淀唯一一个。
之后在普林斯顿大学完成博士学业,现在是普林斯顿大学助理教授。
他的主要研究方向是数论,尤其对p-adic的朗兰兹纲领感兴趣。
值得一提的是,和潘略同一年参加CMO并拿下金牌的陈麟,去年与几位数学家一起完成了几何朗兰兹猜想的证明。
目前陈麟是清华大学丘成桐数学科学中心助理教授。

与潘略同级的几位北大数院校友:梅松(Song Mei)、李超(Chao Li)也都获得了2025年斯隆奖。
而朗兰兹纲领还吸引着诸多中国数学学者,如北大黄金一代中的恽之玮、张伟、袁新意、朱歆文,也正在攀登这一高峰。
论文地址:https://arxiv.org/abs/2502.20645
参考链接:
[1]https://www.quantamagazine.org/the-core-of-fermats-last-theorem-just-got-superpowered-20250602/
[2]https://www.reddit.com/r/math/comments/1l1pttp/the_core_of_fermats_last_theorem_just_got/
[3]https://www.gaokao.com/e/20110110/4d2af5ccc0402.shtml
— 完 —



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


