陶哲轩罕见长长长长长访谈:数学、AI和给年轻人的建议
“AI和菲尔兹奖的距离,只差一个研究生了”
鹭羽 不圆 发自 凹非寺
量子位 | 公众号 QbitAI
陶哲轩罕见接受了一次长长长长访谈,把他关于数学、AI、教育和人类智慧的最新认知,都对外分享了。
作为菲尔兹奖得主,陶哲轩一直被认为是当世最伟大的数学家之一,而这次在与MIT技术背景的播客大神Lex Fridman的对话,也是他近年来首次接受超3小时的非学术机构访谈,内容覆盖数学前沿、AI形式化验证、科研方法论等多个硬核议题。

不仅谈论分享了数学和物理相关的专业性观点,还结合当下AI技术迅速发展的背景,作出了很多像基础教育和AI应用的大众话题思考……
陶哲轩金句频出,比如:
- AI和菲尔兹奖的距离,只差一个研究生了。
- 复数意义上的人类共同体将创造出最顶尖的超级智能体,比单个数学家更有可能实现数学领域的突破。
- 数学的关键在于不仅是找到一个有效的技术路径,而是在几十种可能适用的方法中排除错误答案。
- 科学通常是三者之间的相互作用:现实世界、我们对现实世界的观察,以及我们认为世界如何运作的模型。
- 在理解和看待世界的方式上,数学从公理出发关注模型,物理由结论驱动注重收集结果。
- 在AI的协助下,数学在未来将会有更多的实验,而不仅仅是理论。
- 数学之美在于你可以随心所欲地改变规则,这是其它任何领域都无法做到的一点。
- 解决困难问题就像香港动作片,逐个击破,方得大成。
……
陶哲轩认为,AI正在重塑人类科学范式,数学和物理的终极问题上,AI将成为人类探索这些范式的重要伙伴,但无法取代人类的直觉与创造力。
而关于数学,他也深入浅出地谈论了以下世界级数学难题——
- Kakeya猜想
- 纳维-斯托克斯正则性问题
- 塞迈雷迪定理
- 万物理论
- 广义相对论
- 庞加莱猜想
- 孪生素数猜想
- 克拉兹猜想
- 黎曼假设
- 费马大定理
嗯,是的,这就是一次高智力、高密度和高强度的三高对话,如果你也做好了“大脑尖叫”的准备,一起来看看我们整理过的访谈全文吧~~

访谈陶哲轩全文
本科教育只需要解决10%的问题
Q:你遇到的第一个真正困难的研究级数学问题是什么?
陶哲轩:在本科教育中,你会学到那些真正困难的、甚至看起来是不可能解决的问题,比如黎曼假设、孪生素数猜想。但事实上这并不算什么,真正有趣的是,那些现有技术能完成大约90%的工作,而你只需要解决剩下10%的问题。
在博士期间,Kakeya问题引起了我的注意,事实上这个问题刚刚得到解决,这也是我在早期研究中投入很多的一个问题。历史上,它源于日本数学家Soji Kakeya在1918年左右提出的一个小谜题。
这个谜题是:假设你在平面上时有一根针,或者想象成在路上开车时要执行一个U型转弯,你想在尽可能小的空间内,让这根针调转方向。
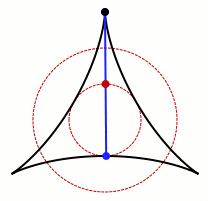
但这根针的移动是无限的,所以可以把它视作一个围绕中心旋转的单位指针。这需要一个面积为π/4的圆盘。
或者你可以做一个三点掉头,实际上只需要π/8的面积。所以,它比旋转更高效。因此,一段时间内,人们认为这是调转指针方向最有效的方法。
但是Besicovitch证明了,事实上可以用任意小的面积来让这根针掉头,比如0.001。所以可以有多种花哨的来回掉头操作,来实现这一点,这样就能让针在掉头过程中穿过每一个中间方向。
这发生在二维平面上。我们理解二维中的一切,那么接下来的问题是,在三维空间中会发生什么?
假设哈勃太空望远镜是太空中的一根管子,如果你想观测宇宙中的每一颗恒星,就需要旋转望远镜以指向每一个方向。
做一个不切实际的构想:假设空间非常宝贵,虽然实际并不是如此,你需要占据尽可能小的体积来旋转你的针,也就是望远镜。那么需要多小的体积才能做到这一点?你可以试图修改基本构造,让望远镜厚度为零,这样就可以使用任意小的体积。
但问题是,如果你的望远镜不是零厚度,而是很薄的厚度delta,那么作为delta的函数,能够看到所有方向所需的最小体积会是多少?
以及随着delta变小,针变细,体积也会减小,但下降速度有多快呢?当时的猜想是它下降得非常非常慢,就像呈对数速度下降,这一点在经过大量工作后也得到了证实。
这个问题有趣的点在于,结果证明它与偏微分方程、数论、几何、拓扑学、组合学中的许多问题都有着惊人的联系。
例如,在波传播中,当你向周围泼洒一些水并溅起水波,它们会向周围各个方向传播,但波同时表现出粒子和波的行为,得到所谓的“波包”,它在空间中非常局限,并随着时间向某个方向移动。如果在空间和时间上绘制它,会显示出一个管状区域。
因此可能会出现,一个最初非常分散的波,在稍后的某个时间节点上,全部聚焦到一点。就像将一颗鹅卵石扔进池塘,涟漪会扩散开。但如果你对该场景进行时间逆转,并且要知道波动方程是时间可逆的,你就可以想象涟漪会汇聚到一个点上,然后发生巨大的飞溅,甚至可能产生奇点。
从几何学上讲,光线也是如此。如果这个波代表光,将波看作是光子的叠加,且光子都沿着光线传播,并且都最终聚焦在一点上。
因此你可以在空间和时间的某个点上,将一个非常分散的波聚焦成一个非常集中的波,但之后它又会再次散开并分离。
但如果该猜想有一个负解,那么这意味着有一种非常高效的方法,可以将指向不同方向的管子打包汇集到一个非常狭窄的小体积区域。
那么你也将能够创造出一些波,它们开始时非常分散,但它们最终不仅会集中在一个点上,在时空中也会有大量的集中点,你将创造出所谓的爆炸,波的振幅将变得相当大,以至于它们所依靠的物理定律不再是波动方程,而是更复杂和非线性的东西。
所以在数学和物理中,我们非常关心某些波动方程是否稳定,是否能够产生奇点。
通过改变物理规律来制造爆炸
Q:您能否谈一下纳维-斯托克斯问题?
陶哲轩:有一个著名的未解决问题,叫做纳维-斯托克斯正则性问题,即控制水等不可压缩流体的流动。
问题在于,如果你从一个平滑的水流速度场开始,它是否会集中到如此大的程度,以至于从某一点开始速度变得无穷大,而这一点就是奇点。当然现实生活中我们不会亲眼看到。
事实上,近年来人们已经达成了共识,对于某些非常特殊的初始构型,比如水,可以形成奇点,只是还未能真正证实。
在克莱基金会的七个千禧年问题中,解决其中一个问题就可获得一百万美元奖金,而这就是其中之一。当中只有庞加莱猜想已经被解决。
所以虽然Kakeya猜想与纳维-斯托克斯问题没有直接联系,但理解Kakeya猜想有助于我们理解波集中这样的问题,这可能会间接帮助我们更好地理解纳维-斯托克斯问题。
这就是数学家区别于几乎所有其他人的地方。如果某件事在99.99%的情况下成立,那么对大多数事情来说,这就足够了。但数学家会关心是否100%涵盖所有情况。大多数时候,水不会爆炸,但也许能设计一个非常特殊的初始状态让它爆炸。
克莱奖问题涉及所谓的不可压缩纳维-斯托克斯方程,它控制像水这样的流体。还有所谓的可压缩纳维-斯托克斯方程,支配像空气这样的流体。
在天气预报中就有很多流体动力学计算,需要收集大量数据以便能够初始化纳维-斯托克斯方程,甚至尽可能求解它,所以它在实际生活中非常重要。
Q:为什么证明方程的一般性结论会如此困难?
陶哲轩:举个例子就是麦克斯韦妖。麦克斯韦妖是热力学中的一个概念,假设你有一个同时装有氧气和氮气的盒子,彼此之间没有隔板阻碍,理应保持混合。
而此时也许会有一个叫做麦克斯韦妖的微观恶魔,促使每次氧气和氮气原子碰撞时,会以某种方式反弹,让氧气全都飘到一侧,而氮气流向另一侧。
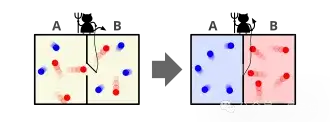
这是一种统计学上的不可能构型,但在数学上经常发生。
例如圆周率π的位数 3.14159……。这些数字看似没有规律,实则从长远看,能看到和4、5、6一样多的1、2、3,理论上不应当偏向某一个数字,但也许π中也存在一个恶魔,当你计算越多位数时,它都会偏向某个数字,但我们目前的技术无法证明。
所以回到纳维-斯托克斯问题,流体具有一定的能量,并且因为流体在运动,能量会被四处传递,同时水具有粘性,如果能量分散在许多不同的位置,流体的自然粘性就会使能量衰减并趋于零。
这在我们实际用水做实验时常会发生,比如泼水时出现的湍流或波浪,最终会稳定下来,振幅越低,速度越小,就越平静。
但也许存在某种恶魔,它不断地将流体的能量推向越来越小的规模,移动速度越来越快,在更快的速度下,粘度影响较小。
因此它可能会创造一种所谓的自相似爆破场景,其中流体的能量从某个大尺度开始,都转移至流体中的一个较小区域,然后以更快的速度移动到更小的区域,依此类推。
每次花费的时间可能是前一次时间的一半,然后可以在有限时间内收敛到集中于一点上的所有能量,即有限时间爆破。
所以如果你有一个大的水漩涡,它往往会分裂成更小的漩涡,但它不会把所有的能量从一个大漩涡全部转移到某一个小漩涡,而是分散转移到三四个小漩涡,小漩涡再各自分裂成三四个更小的漩涡。能量被分散到粘性可以控制一切的程度。
但如果能以某种方式集中所有能量,并且做得足够快,以至于粘性效应没有足够的时间来平息一切,那么爆炸就会发生。
所以有些论文声称,只需要考虑能量守恒,并小心使用粘性,你就可以控制纳维-斯托克斯方程,甚至还可以控制许多类似类型的方程。
所以过去人们多次尝试获得纳维-斯托克斯的全局正则性,这与有限时间爆炸相反,速度需要保持平滑,但所有尝试都失败了,总是存在一些无法挽救的符号错误或其它错误。
所以我感兴趣的是,为什么我们无法证伪有限时间爆破。如果能平均纳维-斯托克斯运动方程,那么我就能关闭某些水的相互作用方式,只保留部分需要的。
特别是如果有一个流体,它可以将能量从一个大涡流转移到小涡流,我会关闭将能量转移到其它漩涡的通道,而只引导它进入该小漩涡,同时仍然保持能量守恒定律。
我希望通过改变物理规律来制造爆炸,这是数学家可以做到的事情。
但也存在数学障碍,所以我做的工作是,当关闭方程的某些部分,它的非线性程度会降低,也会更趋向规则,不太容易爆炸。但我也发现,通过关闭一组精心设计的相互作用,我可以迫使所有能量在有限时间内完成爆炸。
这意味着,如果想要证明纳维-斯托克斯方程的全局正则性,必须利用真实方程所具有的某些特征,而这些特征是我的人工方程所无法满足的。因此某些方法得以排除。
所以数学的关键在于,它不仅仅是找到一个有效的技术并应用它,而是你需要避开那些无效的技术。对于真正困难的问题,通常有几十种你可能认为适用的方法,但只有在积累了大量经验后,你才能意识到这些方法根本行不通。
所以为邻近问题寻找反例,就可以排除掉它,从而节约时间,不会将精力浪费在根本不可能成功的事情上。
我的技术利用的就是超临界性。在偏微分方程中,方程之间就像不同力量在拔河。而在纳维-斯托克斯方程中,有两个相互竞争的项:耗散项和传输项。如果来自粘性的耗散项占主导,那么你会得到正则性。如果传输项占主导,这将是一个不可预测的非线性情况。
但这些力在小尺度上保持平衡,但在大尺度上不平衡。纳维-斯托克斯方程就是超临界方程。在越来越小的尺度上,传输项比耗散项强得多,所以粘性使事物平静下来。
这就是为什么在二维中问题很棘手,苏联数学家Ladyshenskaya在60年代就证明了在二维中没有爆炸,纳维-斯托克斯方程在二维是临界的,即使在非常小的尺度上,传递效应和粘性效应的强度始终大致相同。
我们目前有很多技术来处理临界和次临界方程,并证明其正则性,但对于超临界方程,情况尚不清楚。我对此做了很多工作,也有很多后续研究表明,对于许多其他类型的超临界方程,你可以构造出各种各样的爆炸示例。
一旦非线性效应在小尺度上主导了线性效应,各种坏事都可能发生。所以超临界性与临界性和次临界性会造成了很大的差异。
这是一个关键的定性特征,它区分出一些好的、可预测的方程,比如某些方程可以预测数百万年或者至少数千年的行星运动。但我们无法将天气预测到未来两周以上,因为这是一个超临界方程。因此方程在精细尺度上的非线性非常有趣。
而对于解决纳维-斯托克斯方程,有一种天真的方法,就是不断推动它进入下一个尺度,试图强制让其爆炸。事实证明,这在五维或更高维度中行得通。
但在三维中,我发现了一个有趣的现象,如果你改变物理定律,总是试图将能量推入更小的尺度,能量虽然确实扩展出去了,但上一个尺度上仍然残留有部分能量。结果这使它更容易受到粘性的影响,因此这种直接推进是不可行的。
所以我需要编程一个类似于气闸的延迟,让它在能量推入下一个尺度前一直停留,直到所有能量都被传递到该尺度上,才会开启进入下一个更小尺度的闸门。这样能量就可以逐级推进,抵抗粘性的影响。
当然这需要构造一个相当复杂的非线性项,类似电子电路,利用电阻器和电容器的堆叠,创造一个门,然后利用时钟建立阈值。这类似于鲁布·戈德堡机械,却是用数学描述的,这最终奏效了。
我意识到,也许能在实际方程中完成同样的事情,例如将水的方程式想象成一种蒸汽朋克的东西。类比现代计算机由电子通过非常细小的电线,并与其他电子相互作用实现驱动。
想象水脉冲也以特定速度移动,可能存在两种不同的构型,分别对应开或关。如果让两个运动水体碰撞,它会产生新的构型,比如“与门”或“或门”,这样输出将以一种可预测的方式依赖于输入。
将它们链接起来,也许能创造一台图灵机,一台完全由水制成的计算机。接下来就可以做机器人技术,比如液压等。可以创造一些流体模拟的机器,即冯·诺依曼机。
根据冯·诺依曼移民火星的提议,仅仅光机器运送人力的成本就高得离谱。但如果能运送一台机器到火星,它可以自行开采火星材料并冶炼新机器,那么移民是可行的。
也就是建造一个流体机器,在某种寒冷状态下可以创建自身的更小版本。大的水态机器人会将所有能量转移到更小的构型,然后关机进行自我清理。然后新构型,它会启动并做相同的事情,但更小更快。
而方程具有一定的缩放对称性,可以实现不断迭代。但实际上会让纳维-斯托克斯方程创造一个爆炸。
但现在这只是一个空想,因为有太多缺失的东西使它无法成为现实,例如无法创造基本的逻辑门、没有特殊的水构型、模拟计算总是存在错误、如何关闭大机器的电源而不干扰小机器的写入等等。
它不违背任何物理定律,所以原则上一切都可以发生。当然现在也有其他小组正在追求使纳维-斯托克斯爆炸的方法,他们实际上正在追求更接近直接自相似模型的东西,可以不完全按原样工作,也可能存在有比我刚才描述的更简单的方案来实现它。
生命游戏是一个离散方程
陶哲轩:数学的关键在于,它非常擅长发现一些完全不同的问题之间的联系。只要数学形式相同,就能建立联系。所以以前有很多关于元胞自动机的工作,其中最著名的是康威生命游戏。
存在一个无限的离散网格,在任何给定时间内,网格要么被一个细胞占据,要么是空的,并且有一个非常简单的规则,会告诉你这些细胞如何演化。所以,有时候细胞是存活的,有时候它们是死亡的。
这曾是一个非常流行的屏幕保护程序,实际上就是持续播放这些动画,它们彼此之间相当混乱,甚至有时看起来会像湍流。
但在某个时刻,人们在这个生命游戏中发现了越来越多有趣的结构,例如滑翔机。滑翔机是一个由四五个细胞组成的微小构型,它会像漩涡环一样朝着某个方向进化。
当然这是一个类比,生命游戏是一个离散方程,而纳维-斯托克斯则是一个连续方程,但在数学上它们存在相似的特征。所以随着时间的推移,可以在生命游戏中构建更多有趣的东西。
它是一个非常简单的系统。只需要大约三四个规则就可以实现。再比如有个叫滑翔机枪的东西,它除了吐出一个接一个的滑翔机之外,什么都不做。然后经过科学家的大量努力,终于设法为滑翔机构建了“与门”和“或门”。
这将是一个巨大的荒谬结构,即如果有一串滑翔机流入,另一串滑翔机也流入,那么也许将会有一串新生成的滑翔机流出。但如果只有其中一串含有滑翔机,则不会有输出。
所以一旦你可以构建这些基本门,那么仅仅通过软件工程,你就几乎可以构建任何东西,甚至一台巨大的蒸汽朋克类型的图灵机。
后来人们也确实在生命游戏中生成了可自我复制的巨大机器,一台冯·诺依曼机器,在很长一段时间内,人们认为它的内部就像滑翔机枪在完成计算,因为它会自我创建另一个可以复制的自己。
实际上,这其中很多工作都是由业余数学家们一起完成的。这也是启发我提出在纳维-斯托克斯方程中做同样事情的部分原因。
当然,模拟要比数字差得多,不能直接把生命游戏中的构造放进去。但它也再次说明,这是存在可能性的。
Lex Fridman:细胞自动机中会发生类似于流体的涌现,大规模运作的局部规则可以创造出极其复杂的动态结构。那么其中有任何部分适合进行数学分析的吗?或者是否存在工具加以解释。
陶哲轩: 问题是,只有通过非常精心准备的初始条件,才能获得这种涌现的复杂结构。对于滑翔机枪、门和自推进机器,如果只是随机放置细胞,那么将不会出现此类结构。
这与纳维-斯托克斯方程的情况类似,在典型的初始条件下,不会进行任何奇怪的计算。但通过工程或者以非常特殊的方式专门设计,就可以做出足够聪明的构造。
这在数学中是一个反复出现的挑战,可以称之为结构与随机性之间的二分法,即数学中的大多数生成对象都是随机的,只有极少数事物存在固定模式。
但现在,我们可以通过构造来证明某物存在模式,只要能够证明它确实每隔一段时间就会重复自己一次。例如,你可以证明大多数数字序列都没有模式。只要随机选取数字,就会出现大数定律,它会说明,从长远来看,你会得到和2一样多的1。
但如果给定一个特殊模式,比如π的数字,该如何证明它没有某种奇怪的模式呢?于是我花了很多时间,做的另一项工作是证明所谓的结构定理或逆定理,这些定理将会为事物何时可以变得非常结构化而提供检验。
有些函数是含有加性的,比如你有一个自然数映射函数,可以将2映射到4,3映射到6等。函数的加性意味着如果把两个输入叠加,输出也会相加,例如如果你把a+b乘以10,就等同于把a乘以10和把b乘以10然后相加。
但有些函数并不是完全可加的,例如取数n为10,乘以√2,然后取整,结果约为14点几,取整到14。n为20时则算下来取整到28。此时加性成立,10+10得20,14+14得28。
这种取整方式有时也会存在舍入误差,当把a+b相加时,函数给出的结果并不完全等于两个单独输出的和,而是和加上或减去一。所以此时它几乎是加性的但又不完全加性。
因此我在这上面做了很多工作,大致是如果一个函数表现出类似结构,那么基本上是有原因的,即附近存在一些其他函数。而它自己实际上是完全结构化的。
所以如果你能明确出逆定理,就会创造出二分法,即要么该研究对象完全没有结构,要么它们以某种方式与结构化的东西相关。但无论是哪一种情况,你都可以取得进展。
无限:假设是球形的奶牛
陶哲轩:一个很好的例子是数学中的塞迈雷迪定理,于1970年代得以证明,它涉及在一组数字集合中寻找某种类型的模式,即等差数列,例如3、5、7或10、15、20。
塞迈雷迪证明了,对于任何足够大的数字集合,即正密度集合,都包含有任意长度的等差数列。例如,奇数集合的密度为1/2,则其中包含任意长度的等差数列,因为其实奇数集合相当结构化,我可以轻松找到像11、13、15、17这个等差数列。
塞迈雷迪定理也同样适用于随机集合。如果我取一组奇数集合,然后抛掷一枚硬币,只保留掷出正面的数字,随机去掉一半的数,将得到一个完全没有模式的集合。但由于随机波动,你仍然会在这个集合中找到许多等差数列。
Q:能否证明在随机集合中存在任意长度的等差数列?
陶哲轩: 可以的,比如说无限猴子定理。如果一个房间内有无数会使用打字机的猴子,让它们随机打字,其中一只一定会打出完整的《哈姆雷特》剧本或任何其他有限的文本字符串。这需要相当长的时间,但只要是无限,那么它终会发生。
所以如果你取一个无限的数字串或其他,最终都会呈现出你想要的任何有限模式,只是需要很长时间,等差数列也是如此。
Q:人类应当如何看待无限呢?
陶哲轩:可以把无限视作一个有限数的抽象,而它没有界限。但现实生活中其实没有真正的无限,但你可以假设,比如如果我想有多少钱就有多少钱,想走多快就可以走多快。
数学家就是利用数学将这种形式主义理想化,不是极大或极小,而是无限或零。此时,数学将变得简洁。
在物理学中,我们常常开玩笑地说,假设是球形的奶牛,现实世界中的问题总会受现实世界影响,但你可以理想化,将某些东西送到无限,某些东西送到零,数学就变得容易处理。
Lex Fridman:我想知道使用无穷大有多频繁地迫使我们偏离现实世界的物理规律。
陶哲轩:这里存在很多陷阱。我们在本科数学课上花费了很多时间教授分析学,但分析学是关于如何取极限,例如a+b恒等于b+a,有限项可以交换,但无限项时,如果有一个收敛于某值的级数,重新排列,它将突然收敛于另一个值,则会出现错误。
所以当使用无限时,必须引入ε和δ,以及特定的推理方式,以避免类似错误。
近年来,人们开始对无限极限下成立的结果进行有限化,也就是说,某件事最终将会成真,但无法确定具体时间和速率。
那么如果我没有无限只猴子,而是有限只,我需要等待多久才能看到《哈姆雷特》出来呢?这是一个定量问题,可以用纯粹有限的方法解决,或者利用你的有限直觉。
结果表明,生成的文本长度将呈指数级增长,这也就是为什么你永远看不到猴子写出《哈姆雷特》的原因。也许你能看到猴子们写出了一个包含四个字母的单词,但仅此而已。
所以我发现,当把一个无限的陈述有限化,它就会变得直观得多,也就没那么奇怪了。当然缺点是有限化群要混乱得多,而无限化群在几十年前就得以发现,后来人们才将其有限化。
数学关注模型,物理解释模型
Q:数学与物理学之间,在理解和看待世界的方式上有什么区别?
陶哲轩:我认为科学通常是三者之间的相互作用:现实世界、我们对现实世界的观察,以及我们认为世界如何运作的心理模型。
我们无法直接接触现实,我们只拥有不完整且存在很多误差的观测结果。当我们想要预测的时候,例如预测天气,我们只有简化的模型,有时也只能给出不切实际的假设,就像球形奶牛。
这就是数学模型,数学关注的是模型,而科学收集观察结果并提出解释模型。数学让我们停留在模型内部,并询问模型带来的后果,以及对未来会做出什么预测、是否符合过去的观测数据。而这期间肯定存在共生关系。
数学与其他学科相比,是很不同寻常的,因为数学始于假设,比如模型的公理和模型的结论。但几乎其它学科中,都是始于结论,比如我想建一座桥,然后去找到通往那个结果的路径。这当中很少存在假设,当然推理小说除外。
我们生活中所做的绝大多数事情都是由结论驱动的,包括物理学和科学,例如“这颗小行星会去向哪里?”、“明天的天气会是怎样?”,但数学却是从公理出发。
Q:物理学中存在理论与实验之间的张力,你认为发现有关现实的真正新颖思想的强有力方法是什么?
陶哲轩:需要同时拥有自上而下和自下而上,这是所有事物之间真正的互动关系。随着时间推移,观察、理论和建模都应该更接近现实,即使一开始它们总是相距甚远,只需要拥有其中一个就能弄清楚将另一个推向何方。
因此,如果你的模型预测的是实验未捕捉到的异常情况,它将会告诉实验者去哪里查找更多数据来优化模型,这需要反复操作。
在数学本身中,也存在理论和实验的部分。只是最近,理论几乎完全占据主导地位。99%的数学是理论数学,实验数学非常少。因为假如他们想要研究素数或者其它,可以直接利用计算机生成大型数据集。
就像高斯发现了一个猜想,数论中最基本的素数定理,它预测了一百万乃至一万亿可以有多少个素数。这个问题上,他主要靠自己计算,但也雇佣了人类计算员,用以计算前100000个素数并制作表格,做出预测。
这是实验数学的一个早期例子,但显然理论数学要成功得多,也是直到最近,做一些复杂的数学计算才变得可行。但即便我们现在拥有强大的计算机,也只有一部分数学事物可以通过数值探索。
比如有一种叫做组合爆炸的东西,当你想研究1到1000的所有可能子集,子集数量将会是2 的1000次方,这比目前的任何计算机可枚举的都要大得多。所以有些数学问题无法直接通过暴力计算来解决。
国际象棋则是另一个著名的例子。关于国际象棋排列的数量,我们至今无法用计算机完全解决,但我们现在有AI,它们不会探索博弈树中的每个位置,而是寻求近似值。
事实上人们现在就正在使用这种国际象棋引擎来做实验性国际象棋。他们正在重新审视古老的国际象棋理论,例如传统的经典开局,也许并不是最优解,他们希望用国际象棋引擎来实现改进。
我希望数学在未来会有更大的实验成分,也许将由AI驱动。
数学的不合理但有效
Lex Fridman:你提到了柏拉图的洞穴寓言。如果人们不知道洞穴是人们观察现实的影子,而不是现实本身,并且他们相信他们所观察到的就是现实——从某种意义上说,这是数学家和也许所有人类都在做的事情,即观察现实的影子——我们有可能真正接触到现实吗?
陶哲轩:这当中存在三个本体论的东西,分别是实际的现实、我们的观察和我们的模型,严格来说它们彼此不同,而我认为它们将永远不同。但它们会随着时间逐渐靠近,但在靠近的过程中必须舍弃掉你最初的直觉。
例如在天文学中,最初人们认为世界模型是平的,因为它看起来很平,且很大。而宇宙的其余部分,即天空,则看起来很小。所以当你从模型出发,它实际上与现实相去甚远,但它又符合当下你的观察结论。
但随着时间推移和越来越多的观察,模型将更接近现实,我们也会意识到地球是圆的,它在旋转,并围绕着太阳系运行,而太阳系围绕着银河系运行,而宇宙在膨胀,膨胀本身也在加速膨胀……但事实上就在今年,我们发现宇宙的加速也是非恒定的,由于暗物质或暗能量这类东西的存在。
我们有一个数据拟合相当好的模型,在某种程度上可以解释它。该模型只有几个你必须指定的参数。但人们会说,那是捏造因子,有足够的捏造因子,你就可以解释任何事情。可是数学的观点是,希望模型中的参数要比观测数据集中的数据点少。
如果一个模型有10个参数,可以解释10个观测结果,该模型将完全无用,这叫做过拟合。而如果你的模型只有两个参数,却解释了1万亿个观测结果,这就是暗物质模型,我认为它有14个参数,可以解决天文学家拥有的PB级数据。
所以你可以把一个物理数学理论看作是对宇宙的一种数据压缩,即把这些PB级数据压缩为一个可以用五页纸描述的模型,并指定一定数量的参数,如果它能以合理的精度拟合几乎所有的观测结果,那么压缩越多,你的理论就越好。
爱因斯坦说过这样一句话:“宇宙中最难以理解的事情是它是可理解的。”,这就是数学的不合理但有效。
实际上这里有一些可能的数学解释,比如数学中有一种叫做普适性的现象。许多宏观尺度上的复杂系统都是从大量微观尺度上的微小相互作用中产生,而由于组合爆炸,你会认为宏观尺度的方程一定比微观尺度的方程指数级复杂。
如果要完全精确地求解,比如模拟一盒空气中的所有原子,就像阿伏伽德罗常数这将会是巨大的,如果你真的试图跟踪每一个粒子,这将是荒谬的。
但某些定律只在微观尺度上涌现,几乎不依赖于宏观尺度上发生的事情,或者只依赖于非常少的几个参数。所以,如果要模拟盒子里包含万亿粒子的气体,只需要知道它的温度、压力、体积以及五六个参数,就可以模拟10^23或任何数量的粒子的所有信息。
因此,我们无法在数学上理解普适性,但存在一些可以帮助我们理解普适性发生原因的玩具模型,例如中心极限定理就解释了为什么钟形曲线在自然界中无处不在,那么多事物都是高斯分布。
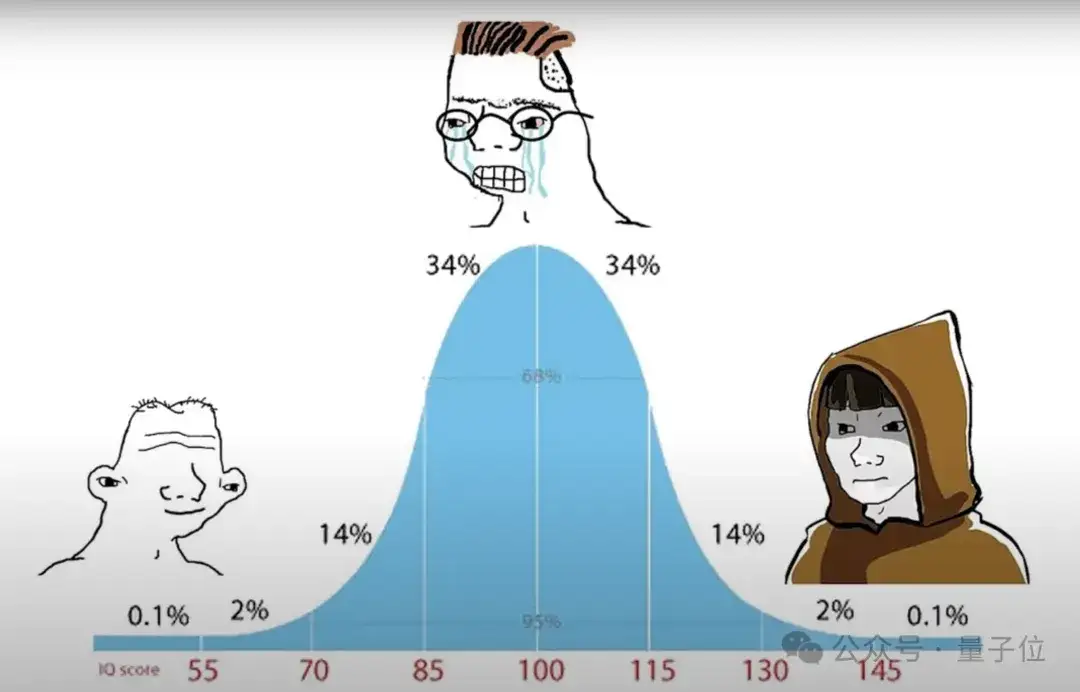
现在甚至还有一个携带钟形曲线的模因,甚至模因也具有普适性。如果你愿意,你可以选择元,但存在许多过程,比如选取很多独立的随机变量,以各种方式将它们平均在一起,取简单平均或更复杂的平均,我们就可以在各种情况下证明高斯曲线的出现。
但如果你有许多不同的输入,且它们之间存在某种系统关联,则可能得不到钟形曲线,所以普适性并不是100%可靠。
全球金融危机就是这方面的一个著名例子。人们认为抵押贷款违约的行为存在高斯曲线,如果在拥有抵押贷款的十万美国人中,询问违约比例,如果一切都是去相关的,将会生成漂亮的钟形曲线,然后你可以用期权和衍生品管理风险。
但如果经济中存在系统性冲击,推动所有人同时违约,那将是非常反高斯的行为,这就是2008年没有被充分考虑进去的后果。
我认为,现在人们更多地意识到,系统性风险实际上是一个更大的问题,模型很漂亮,但它可能不匹配现实。所以研究模型行为的数学非常重要,但也需要科学来验证它何时符合现实,何时不符合。两者都被需要。
而数学可以提供帮助,因为像中心极限定理就会告诉你,某些假设的输入之间如果不相关,那么你就会拥有高斯行为。它也会告诉你到哪里去寻找模型中的弱点。
所以如果你理解中心极限定理,就可以使用高斯行为或其它来模拟违约风险,如果你受过数学训练,你就会寻求输入之间的系统相关性,并询问经济学家这样存在多大的风险,然后你就可以继续了。所以在科学和数学之间总是存在这种协同作用。
Q:是否存在一种可以将不同领域的数学连接起来的底层结构?
陶哲轩:肯定存在相互联系的线索,数学的很多进展都来自于将两个先前没有联系的数学领域联系起来。一个古老的例子是几何和数论。在古希腊时代,它们并不被认为是相关的,直到笛卡尔意识到并发展了解析几何,可以用两个实数来参数化几何对象平面。几何问题最终可以转化为数字问题。
当然今天这两个领域已经统一了,类似的过程也在数学中反复上演,代数和几何曾是分开的,现在又有了代数几何。
我认为数学家也有各种风格,就像刺猬和狐狸,狐狸知道很多事但都只懂一点,而刺猬只知道一件事但知道得很深。理想的数学家合作就需要多样性,让一只狐狸与多只刺猬合作,或者反之亦然。
我主要认为自己是一只狐狸,我很喜欢套利这个金融说法,学习一个领域是如何运作的,了解该领域的技巧,然后去到另一个不相关领域,但我可以自行调整这些技巧,看到领域之间的联系。
所以还存在许多比我研究更深的科学家,他们是真的刺猬,了解一个领域的一切,且在那个领域更快、更有效,而我可以给他们提供额外的工具。
而两种思考之间,我更倾向成为狐狸,我喜欢寻找类比、叙述。假如我看到一个领域的结果并且很喜欢,但我不喜欢证明,尤其是它使用了我不是很熟悉的数学类型,我将经常会尝试用我喜欢的工具重新证明它。
通常我的证明更糟糕,但通过这样练习,我可以充分明白另一个证明试图在做些什么。由此我可以对那个领域使用的工具有所理解。这是非常具有探索性的,非常像是在疯狂的领域里做疯狂的事情,并且像是在大量重新发明轮子。
刺猬风格也会更学术,你将会非常注重知识,及时了解这个领域的所有进展。了解所有历史并对每种特定技术的优缺点有很好的理解。你会更依赖计算而不是试图寻找叙述。当然我也可以那样做,但始终有其他人在那方面更为擅长。
Q:你是在什么时候意识到数学可以有一种优雅和美感的?
陶哲轩:当我来到普林斯顿读研究生时,John Conway当时也在那里,他于几年前去世了。但我记得我参加的最早的研究讲座之一,就是Conway关于他的极端证明的报告。
Conway会以一种你通常不会想到的方式思考各种事物,他认为证明本身就占据了某种空间,所以如果你想证明某件事,比如说有无限多个素数,你可以把它们放到不同的轴上。
有些证明是优雅的,有些证明很长,有些证明是初级的。这样就有了证明空间,且空间本身具有某种形状。他对形状的极值点很感兴趣,比如在所有证明中,什么是以牺牲其他一切为代价的最短证明?或者什么是最初等的证明?或者其它。
所以他列举了一些著名定理的例子,然后他会给出他认为是这些定理的极端证明。这真的让人大开眼界,这不仅是得到一个有趣的结果证明,而且一旦你有了这个证明,试图用各种方式优化它,证明本身就拥有了一些技巧。
这也影响了我的写作风格。比如当你做本科数学作业时,你被鼓励写下任何有效的证明并交上去,得到一个勾,你就继续前进。
但如果你希望你的结果真正具有影响力并被人们阅读,它就不能只是正确的。它也应该让阅读成为一种享受,才能有动力推广到其他事物。
这和许多其他学科一样,比如像编码。数学和编码之间有很多类比。就像你可以用意大利面条式代码编写一些东西,它适用于某个任务,又快又脏而且高效。但其实有很多可以写好代码的好原则,这样其他人就可以使用它,并在此基础上构建,减少错误的发生,数学也有类似的事情。
另外还有一种叫做代码高尔夫的活动,我也觉得它美丽而有趣。人们使用不同的编程语言,来试图写出完成特定任务的最短程序。我甚至相信这里存在一个比赛,不仅可以对程序进行压力测试,还可以对证明或者不同语言进行测试。也许这是一种不同的符号,用以完成不同的任务。
Lex Fridman:你觉得数学中最美丽或最优雅的方程是什么?欧拉恒等式常被认为是数学中最美丽的方程,你是否在那个方程式中,在欧拉恒等式中找到了美?
陶哲轩:我来说的话,我觉得最吸引人的是不同事物之间的联系,欧拉恒等式使用了所有的基本常数,这很可爱。但对我来说,指数函数是欧拉引入来测量指数增长的,所以复利或衰减,任何持续增长、持续减少、膨胀或收缩的东西,都可以用指数函数建模。
而π来自圆和旋转,如果你想转一根针180度,你需要旋转π弧度。而i复数表示虚轴上的摆动,对应90度的旋转,所以是方向上的改变。所以指数函数代表当前方向上的增长和衰减。当你在指数中加入i时,它现在变成与当前位置成直角的运动。
然后欧拉恒等式将告诉你,如果你旋转一个时间π,你最终会得到另一个方向。它将通过复化和i的旋转,将所有数学工具统一起来,包含数学、动力学、几何和复数。
而当你第一次研究任何东西时,你必须测量事物并为它们命名,有时因为模型与现实相去甚远,也会给错误的东西起了好名字,但直到后来你才发现什么是真正重要的东西。
例如在物理学中,E=MC²,其中一件大事就是E,而当亚里士多德首次提出运动定律,然后是伽利略或牛顿能测量质量、加速度、力等等,所以有了著名的牛顿第二运动定律F=ma。因为这些是主要对象,所以它们被赋予理论中的核心位置。
直到后来人们开始分析这些方程,才发现似乎这些量总是守恒的,特别是动量和能量。而事物是否拥有能量,这并不明显,能量它不像质量、速度那样可以直接测量,但随着时间推移,人们逐渐意识到这实际上是一个非常基本的概念。
哈密顿最终在19世纪将牛顿物理定律重新表述为哈密顿力学,其中能量,也就是哈密顿量是主导对象,一旦你知道如何测量任何系统的哈密顿量,你就能完全描述动力学,即所有状态会发生什么。
它作为核心角色,起初也并不明显,而当量子力学出现时,视角的转变则提供了很大的帮助。研究量子力学的早期物理学家,他们首先尝试将牛顿力学融入量子力学,但遇到了很多麻烦,因为一切都是粒子,而我认为它是波,总之结合起来非常奇怪。
如果你问,F=ma的量子版本是什么,这很难回答。但事实证明,在经典力学背后的哈密顿量也是量子力学的关键对象,这里也有一个叫做哈密顿算符的对象。它是一种不同类型的对象,是运算符而不是函数,但一旦指定了它,你就指定了整个动力学。
所以这里有一个叫做薛定谔方程的东西,它可以准确地告诉你,一旦你拥有哈密顿量,量子系统将会如何演变。
所以将二者放在一起,看起来是完全不同的对象,一个涉及粒子,一个涉及波。但有了中心性,就可以将很多直觉和事实从经典力学转移到量子力学。
例如,在经典力学中,有一个叫做诺特定理的东西。每当物理系统中存在对称性,就有出现守恒定律。所以物理定律是平移不变的。
比如如果我向左移动10步,我会体验到与初始位置相同的物理定律,这对应动量守恒。而如果我以某个角度转身,我又将再次体验到相同的物理定律。这对应角动量守恒。如果我等待10分钟,我仍然有相同的物理定律,由于存在时间平移不变性,这对应能量守恒定律。
所以在对称性和守恒之间存在这种基本联系,这在量子力学中也成立。尽管方程完全不同,但因为它们都源于哈密顿量,哈密顿量控制一切。当每次哈密顿量具有对称性时,方程就会有一个守恒定律。所以一旦你拥有正确的表述,很多事情都变得清晰起来。
我们无法统一量子力学和广义相对论,因为我们还没有弄清楚基本对象是什么,例如我们必须放弃空间和时间的概念,因为这些空间几乎是欧几里得类型,只在非常小的尺度上出现量子涨落,从而形成时空泡沫,试图用笛卡尔坐标xyz解释是行不通的,但我们还不知道用什么来代替它。我们没有类似于哈密顿量能组织起一切的类似数学概念。
直觉就在那里,你必须转移它
Q:你的直觉是否认为存在一个万物理论,可以找到一个统一广义相对论和量子力学的语言?
陶哲轩:我相信如此。多年来,物理学的历史就是统一的历史,就像数学一样。例如电和磁是分开的理论,然后麦克斯韦统一了它们。牛顿统一了天体的运动与地球上物体的运动。等等诸如此类,都说明了统一时有发生。
再次回到这个观察和理论的模型,我们物理学的两个大理论,广义相对论和量子力学,现在发展如此之好,加起来涵盖了我们所能做的所有观察的99.9%。
你现在要么去研究极其疯狂的粒子加速器,或者早期宇宙,再或者那些知道很难以测量的东西,才能偏离这两个理论中的任何一个,直到你真正弄清楚二者如何结合在一起。
但我相信,我们已经这样做了几个世纪,我们在以前也已取得一定进展,没理由我们应该放弃。
Q:您认为您会成为一名发展万物理论的数学家吗?
陶哲轩:经常发生的情况是,当物理学家需要一些数学理论时,通常数学家们已经研究出了一些前身理论。
所以当爱因斯坦开始意识到空间是弯曲的,他去找一些数学家询问弯曲空间理论是否可用,然后他说,他认为黎曼发展了黎曼几何学,这恰恰是一种空间以各种一般方式弯曲的理论。事实证明,这就是爱因斯坦理论几乎完全需要的。
这就又回到了数学的不合理的有效性,那些能很好地解释宇宙的理论,往往也能很好解决具有相同数学对象的数学问题。归根结底,它们只是组织数据的两种有效方式。
而弦理论,虽然几十年来一直保持领先,但我认为它正在慢慢退出历史舞台,因为它与实验并不匹配。
Lex Fridman:当前最大的挑战之一就是实验非常困难,因为两种理论都如此有效,但另一方面,你所谈论的不仅是偏离时空,更是进入一些疯狂的维度,你现在所做的事情,对我们来说,已经距离我们认为地球是平坦的时候相隔甚远,我们很难用有限的认知来感知那个所谓的现实到底是什么。
陶哲轩:这就是为什么类比如此重要。圆形的地球并不直观,因为我们被困在其上,但我们对圆形物体以及光的工作原理有相当好的直觉。
实际上,这是一个很好的练习,为了真正弄清楚日食、月相是如何发生的,可以用圆形地球、圆形月亮的模型很轻松地解释。你可以拿一个篮球、一个高尔夫球和一个光源,自己实际去做这些事情,直觉就在那里,你必须转移它。
现代科学也许是自身成功的受害者,为了更加准确,需要离最初的直觉越来越远。因此,对于没有经历过科学教育的人来说,这个过程显得相当可疑,因此我们需要更多科学基础。
有些科学家做了相当出色的外出推广工作,但在家里也可以做很多科学的事情。YouTube上有很多视频,我最近就和Grant Sanderson一起做了一个YouTube视频,我们讨论古希腊人如何能够测量到月球的距离、到地球的距离,并使用你自己也可以复制的技术,不一定是花哨的太空望远镜或令人生畏的数学。
改变视角真的很重要。旅游可以拓宽思维,而这就是智力旅行,你把自己放在古希腊人或者其它时期的人的脑海中,做出球形奶牛的假设,这是数学家所做的,也是一些其他艺术家正在做的。
如果你提出公理,那么数学会让你遵循这些公理并得出结论,有时你将可以从初始假设中走得很远。
想象自己是个矢量场
Q:能否从数学的角度解读广义相对论,它的那一方面让你感兴趣,对你来说具有挑战性?
陶哲轩:我研究过一些方程。有一个叫做波映射方程或西格玛场模型的东西,它并不完全等同于时空引力本身的方程,而是某些可能存在于时空之上的场的方程。
所以爱因斯坦的相对论方程只描述时间和空间本身,但还有其他场存在,比如电磁场、杨-米尔斯场,以及一整套不同的方程。
其中爱因斯坦方程被认为是最非线性和困难的方程之一,但在层次结构中相对较低的,是这个叫做波映射方程的东西。
这是一个波,在任意给定点上都像是被固定在一个球体上。所以我可以想象时空中有许多箭头,这些箭头指向不同的方向,像波浪一样传播。如果你摆动其中一个箭头,它会传播并使所有箭头移动,这有点像麦田里的麦浪。
我对这个方程的全局正则性问题很感兴趣,那么是否可以让所有能量集中于一点呢?所以我考虑的方程实际上是所谓的临界方程,它实际上在所有尺度上的行为都大致相同。我勉强证明了,你实际上无法强迫所有能量都集中到一点上,能量必须在此刻稍微分散一点,而一旦它分散一点点,它就会保持正则。
是的,这是在2000年发生的事。所以这其实也是我后来对纳维-斯托克斯方程感兴趣的部分原因。我开发了一些技术来解决这个问题,所以得出的部分结论是由于球体的曲率,这个问题实际上是非线性的,存在一种非微扰效应。
当你正常观察它时,它看起来比波动方程的线性效应更大,即使你的能量很小,也很难将其控制。
但我开发了一种叫做规范变换的东西,方程有点像麦浪的演化,它们都在来回弯曲,存在很多运动。但如果想象一下,通过在空间的不同点上,附加小摄像机来稳定流动,这些摄像机试图以捕捉大部分运动的方式移动,在这种稳定的流动下,流动将会变得线性得多。
我发现了一种可以减少非线性效应量的变换方程,然后我就能够求解这个方程了。这是我在澳大利亚拜访我的姨母时,发现的这个变换,当时我试图理解所有这些场的动力学,但我无法单单用纸笔完成,也没有足够的计算机设备来做任何计算机模拟。
所以我最终闭上眼睛,躺在地板上,想象自己实际上是个矢量场,然后来回翻滚,试图找到如何改变坐标,让各个方向的事物都能以合理的线性方式运行。
当我这样做时,我的姨母走进来问道,我在做什么。我回答说,这很复杂。于是姨母说,好吧,你是年轻人,我不多问了。
学会策略性“作弊”
Q:你是如何解决难题的,是否在脑海中经常可视化数学对象、符号?
陶哲轩:有很多的纸和笔。作为一名数学家,我学到的一件事情是,策略性作弊。
数学之美在于你可以随心所欲地改变规则、改变问题,这是其它任何领域都无法做到的一点。如果你是一名工程师,有人说,在这条河上建造一座桥,你不能说,我想在这里建一座桥或者我想要纸而不是钢来建造它,但作为数学家,你可以做任何你想要做的事情。
这就像试图通关一个电脑游戏,其中有无限的作弊码可用。你可以自行设置,例如有一个很大的维度,我可以先将其设为一,先解决一维问题,因此存在一个主项和一个误差项,所以我需要做一个球形奶牛假设,假设误差项为零。
所以当你试图寻找解决问题的方法,不应该在铁人模式下进行,让事情变得最大化困难,更合理的解决方式是,如果有10件事让你的生活变得困难,你可以先找到其中一个问题并关闭另外九个困难。
这样你就安装了九个作弊码,而如果你安装了十个作弊码,那么这个游戏将是微不足道的。当你安装九个,然后集中解决那一个问题,它将教会你如何解决那个特定的困难,然后你关闭这个,再打开其它问题并依次解决。在你最终学会如何分别解决这10个问题后,再将其中几个合并处理。
小时候,我看了很多我们文化中的香港动作片,每次遇到打斗画面,例如英雄会被一百个坏蛋喽啰包围,在精心设计的场景下,他一次只会与一个人战斗,打败那个人后再继续前进。正因为如此,他可以打败他们所有人。
但是,如果这群人更聪明一点,就应该直接蜂拥而上,当然这样电影效果会很糟糕,但他们会赢。
Q:你通常是使用纸和笔工作吗?是否会使用计算机和LaTeX工作?
陶哲轩:实际上主要是纸和笔。在我的办公室里,我有四块巨大的黑板,有时候只需要把我所知道的关于问题的所有信息都写在这上面,然后我会坐在沙发上,看着整个东西。
其中有很多绘画和只有自己能理解的定制涂鸦。黑板的美妙之处在于可以擦除,但现在我也开始越来越多地使用计算机,部分原因是因为AI能执行简单的编码工作,让事情变得更加容易。
以前如果我想要绘制一个中等复杂度的函数,包含一些迭代或其它东西,我必须记住如何设置Python程序、以及循环如何工作并调试它,这需要两个小时的时间。但现在我可以在10到15分钟内完成,所以我现在使用越来越多计算机进行简单的探索。
总有算法来负责将一棵树和另一棵树进行匹配
Q:可以描述一下Lean形式化证明编程语言吗?以及它是如何作为证明助手提供帮助的?
陶哲轩:Lean是一种计算机语言,就像Python和C等标准语言一样,但在大多数语言中,重点在于产生可执行代码。代码行会执行一些操作,例如翻转比特、让机器人移动或在互联网上发送文本等。
而Lean也是可以做到这一点的语言,可作为一个标准的传统语言运行,但它也能生成证书。像Python这类软件可能会进行计算并告诉你3+4的答案是7,但Lean不仅可以生成答案,还能生成它是如何得到7的证明,以及其中涉及的所有步骤。
它创建了更为复杂的对象,不仅仅是陈述,而是带有证明的陈述。每一行代码都只是将先前的陈述拼凑在一起,然后创建新陈述。
这个想法并不新鲜,它们被称为证明助手。它们提供语言,让你可以创建相当复杂精细的数学证明。如果你的编译器可信,那它们会生成证书,确保你的观点100%正确,但它们也会让编译器变得非常小,并且有多个不同的编译器可用。
Q:你是否可以描述一下在纸笔上书写和使用Lean编程语言之间的区别?形式化一个陈述有多难?
陶哲轩:很多数学家都参与了Lean的设计,所以它被设计成单独的代码行,类似于数学论证的单独行。比如你可能想引入一个变量,证明一个矛盾。有很多你可以做的标准操作,理想情况下应该是一一对应的,但实践中并非如此。
Lean就像向一个极其迂腐的同事解释一个证明,他会指出,你真的是这个意思吗?如果这个是零怎么办?你如何证明这个?而Lean中包含很多自动化功能,可以减少麻烦。
例如,每个数学对象都必须包含一个类型,比如谈论X,X是实数、自然数,还是函数或者其它,如果非正式数学,它通常需要有上下文,例如“显然X是Y和Z之和,Y和Z是实数,那么X也应该是实数。”
Lean可以做很多类似的事情,每隔一段时间它就会说,你能告诉我更多关于这个对象是什么的信息吗?它是什么类型的对象?所以你必须在哲学层面上思考更多,不仅仅是你正在做的计算,而是每个对象在实际意义上代表什么。
Lex Fridman :它是使用LLM进行类型推断吗?还是可以与实数匹配?
陶哲轩:它使用了更传统的老式AI。你可以把这些东西都表示成树,总有算法来负责将一棵树和另一棵树进行匹配。每个物体都有历史可以追溯。
Lean是为可靠性而设计的,所以现代AI没有被用在里面,它是一个完全不相关的技术。
所以当一个数学家试图在Lean中编程一个证明时,通常会有这样一个步骤,比如“好的,我现在想要使用微积分的基本定理来做下一步。”
所以Lean开发者构建了这个庞大的项目mathlib,它是一个包含数万个有关数学对象有用事实的集合,其中就有微积分基本定理,但你需要找到它,所以现在的很多瓶颈是引理搜索。
你可以有各种专门用于数学引理搜索的搜索引擎,但现在有了这些大型语言模型,你就可以直接询问它们,例如当我编码时,我在我的IDE中安装了GitHub Copilot作为插件,它会扫描我的文本,看到我的需求。
当我需要使用微积分基本定理时,它会提供建议,25%的时间它完全正确,另外10-15%的时间它不完全有效,但足够接近,然后我会告知它需要修改的地方,它就会生效,然后大约有一半的时间,它给我的是完全的垃圾。但人们开始在上面使用一点点人工智能,主要在自动补全的层面上,你可以输入证明行的一半,让它告知你另外一半。
所以我现在估计,将一个证明形式化出来所需的时间和精力大约是写出来所花费的时间和精力的10倍,它是可行的,但很烦人。
这是它唯一迂腐的地方,但在某些情况下,形式化地做事情实际上更愉快。有一个我形式化了的定理,在最终陈述中存在常数12,12必须贯穿整个证明,所有其它数字都必须与这个最终数字12保持一致,所以我们写了一篇围绕着数字12的定理文章。
然后几周后,有人说可以通过重新处理其中一些步骤,将12改进为11。当这种情况发生在纸笔上时,每改变一个参数,就必须逐行检查证明的每一行是否仍然有效,并且可能存在一些你没有意识到的微妙之处,你没有意识到你在利用12的某些性质,所以一个证明可能在微妙之处崩溃。
所以我们用常数12形式化了这个证明,当新论文出来时,花了我们20个人大约3周时间形式化。然后现在将12更新到11,在Lean里面直接修改就行, 然后运行编译器,在所拥有的数千行代码中,90%仍然有效,只有少数几行标红。
现在我无法证明这些步骤的正确性,但它立即隔离出哪些步骤你需要改变,你可以跳过所有正常工作的部分,只会有一小部分地方需要你修改。所以在一两天内,我们就把我们的证明更新到了11。这是一个非常快的过程,比纸笔要顺利得多。
由于证明更长,每个单独的部分更容易阅读。例如当你拿到一篇数学论文,跳到第27页,看第6段,这里有一行数学文本,我常常不能立即读懂它,因为它假设了各种定义,我必须回去去找,也许10页前定义了这个,证明总是分散在各处,所以你基本上被迫连续阅读。
它不像小说那样,可以打开一半开始读,这里存在很多上下文。但当证明在Lean中时,如果你把光标放在某一行代码上,那里的每个对象,你都可以让光标悬停,它会说出这是什么,来自哪里,在哪里被证明。这比翻阅数学论文更容易回溯事物。
所以,Lean真正实现的一件事是,在原子尺度上协作证明,这在过去是无法做到的。所以传统上,当你想与另一位数学家合作时,要么在黑板前进行真正的互动,要么通过电子邮件或其它方式,但必须进行分段,例如我要完成第3节,你做第4节,但不能真正在同一时间在同一件事上协作工作。
但有了Lean,你就可以尝试形式化证明某一部分,然后说,我在第67行卡住了,我需要证明这个东西,但它并不完全有效,这是我有麻烦的三行代码。由于所有上下文都在那里,别人可以说,好的,我知道你需要做什么,你需要应用这个技巧或这个工具。
你可以进行极其原子级别的对话。因为Lean,我可以与世界各地的几十个人合作,其中大多数人我从未见过面。实际上我也不知道他们在过程中是否可靠,但Lean给了我一份信任证书,这样我就可以进行无信任数学。
Q:在合作时,解决数学难题的正确方法是什么呢?是分而治之,还是你会专注于某个特定部分,并且正在头脑风暴?
陶哲轩:首先总是有一个头脑风暴过程。对于数学研究项目,本质上从一开始,你真的无从下手。它不像一个工程项目,理论已经确立了几十年,实施才是主要困难。你甚至必须弄清楚什么是正确的路径。
就像我之前说的“作弊”,回到建桥的类比,首先假设你拥有无限的预算和无限的劳动力,现在你能建这座桥吗?那现在有无限的预算但只有有限的劳动力,现在你能做到吗?当然没有工程师能真正做到这一点,因为他们有固定的要求。
在项目开始你总是会尝试各种疯狂的事情,做出所有不切实际的假设,但你计划稍后再来修正解决。然后你会尝试看看是否存在一个可能有效的方法框架,并寄希望于将问题分解为更小的子问题,然后你就可以专注于子问题。
有时不同的合作者更擅长处理某些事情。例如我和本·格林的一个定理,叫做格林-陶定理(the Green-Tao theorem)定理。它是一个关于素数包含任意长度的等差数列的陈述,这是对塞迈雷迪定理的一个修改。
而我们合作的方式是,本已经证明了长度为3的等差数列含有一个类似的结果。他表明,像素数这样的集合包含大量长度为三的数列,甚至素数的某些子集也包含。但他的技术只适用于长度为三的数列,不适用于更长的数列。
但我有这些来自遍历理论的技术,这是我当时一直在玩的技术,我比本更熟悉。所以如果我能证明某些与素数相关的集合的特定随机性性质,就存在一定的技术条件拥有它。如果本能为我提供这个事实依据,我就可以得出定理。
但我要的是数论中一个非常困难的问题,他说我们不可能证明出来这个,所以他说,你能用一个弱假设来证明你的那部分定理吗?他提出了一些他可以证明的东西,但对我来说太弱了,我不能用这个。所以类似的对话来回进行。
我们之间存在不同的作弊方式,我想作弊更多,他想作弊更少。但最终我们找到了一种属性:A、他能证明;B、我可以使用,然后我们就可以证明我们的定理。所以要知道每次合作都会发生一些故事,没有两次完全相同。
Lean可以帮助科学家大规模地生产实验结果
Q:如何看待Lean这一类编程语言?
陶哲轩:目前只有少数数学项目可以以这种方式划分,在当前的技术水平下,大部分的Lean活动都是在形式化人类已经证明的定理,基本上一个数学论文就是一个定理或一种意义上的蓝图。
Lean可以将一个困难的陈述,比如一个大的定理,分解成100个小的引理,但通常不是所有的定理都写得足够详细以至于每一个都可以直接分解。
而蓝图就像一份非常繁琐的论文,其中每一步都尽可能详细地解释,并试图使每一步都相对独立,仅依赖于少数几个已证明的前置陈述,因此蓝图中的每个节点都可以独立处理,甚至不需要了解整个系统的运作方式。
嗯,这就像现代供应链,如果你想要制造一部 iPhone 或其他复杂物体,没有人能够独立完成整个物体,但你可以让一个专家,如果他们从其他公司获得一些部件,就能将它们组合成稍大一些的部件。
Lex Fridman:我认为这是一个非常令人兴奋的可能性,因为如果找到可以按这种方式分解的问题,就能拥有分布在全球各地的、成千上万的贡献者,是这样么?
陶哲轩:对的。目前大多数数学都是理论性的,而实验性数学则相对较少,我认为像Lean和其他软件工具,比如GitHub之类的,将允许实验数学以比我们现在所能做到的更大程度进行规模化。
现在如果你想要做任何关于数学模式或什么的数学探索,你只需要写一些代码来描述这个模式。我的意思是,有时候有一些计算机代数软件包会提供帮助,但通常只是由一位数学家编写大量的Python或其他代码。毕竟编程是一项容易出错的活,所以让其他人协作编写你的代码模块并不实际,因为如果其中一个模块有bug,整个系统就不可靠。
这些定制的意大利面条式的代码,由不是专业程序员而是由数学家编写的,它们笨拙而且缓慢,所以很难大规模地生产实验结果。但是有了Lean,数学家就能更好地进行这些工作。我有一个项目叫方程理论项目,在这个项目中我们生成了大约 2200 万个抽象代数的小问题。
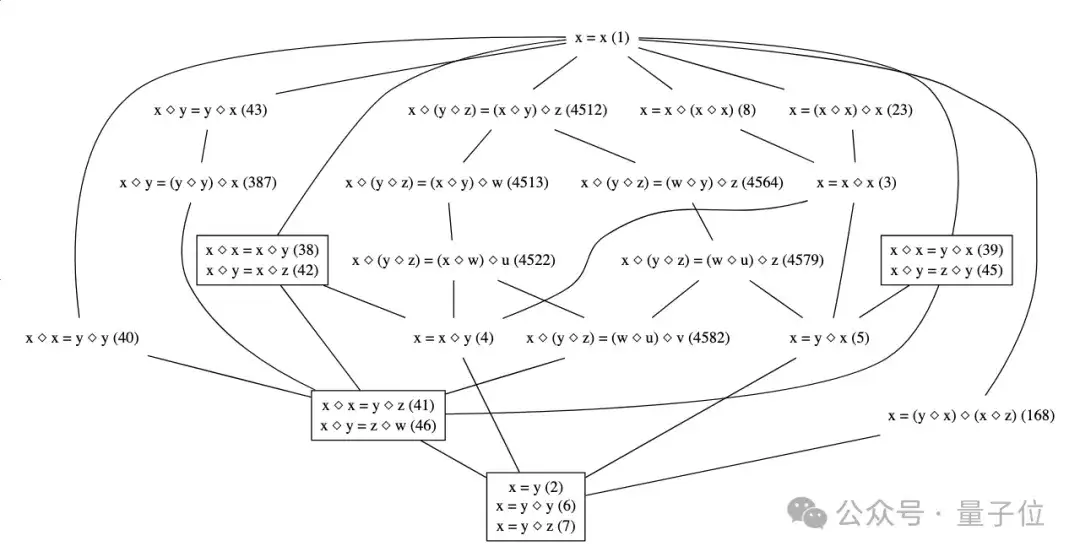
△图片来源于方程理论项目页
抽象代数研究乘法和加法等运算以及抽象的性质,比如乘法的交换律,XY总是等于YX,至少对数学来说是这样,这些运算遵循一些其它运算不遵循的法则。但并非所有的法则都是通用的,任何操作都可能遵循其它操作不遵循的法则,所以我们生成了大约4,000种可能的代数法则,以适应不同的运算。
我们的问题是哪些法则会隐含哪些其他法则?嗯,例如,交换律是否隐含结合律?答案是否定,因为事实证明你可以描述一个操作,它遵守交换律但不遵守结合律,但另外一些法则确实蕴含其它法则,有时它们可以彼此替换,可以用一些代数进行证明。因此我们研究了这4000条法则之间的配对,大约有2200万对组合,对于每一对我们都会问:这条法则是否蕴含了那条法则?如果是,请给出证明;如果不是,请给出反例。
这2200万个问题,每一个问题都可以交给一个本科生代数学生,他们有相当大的机会能够解决这些问题。尽管在这2200万个问题中,有少数几个,比如100个左右,确实非常难,但是很多问题都很简单。这个项目的目标就是确定整个图里哪些法则暗示了其它的法则。
Lex Fridman:这真是一个了不起的项目,一个好主意、好测试。这正是我们一直在讨论的问题,规模令人瞩目。
陶哲轩:是的,所以这种事情交给人工是不太可行的,我的意思是,最先进的技术在文献中大约会有15 个方程以及它们的应用方式,这差不多就是人类研究论文所能达到的极限了。如果你需要将规模扩大,就需要把这个项目众包,还需要信任——没有人能检查 2200 万个这些证明。你需要实现自动化,这只有在有了Lean之后才成为可能。
我们也希望大量使用人工智能,所以这个项目已经接近完成了:在这2200万个证明中,只剩下2个没有得到解决。而实际上,关于这两个,我们有两份纸笔证明,今天早上我还在努力完成它。所以这个项目我们几乎完成了。
Lex Fridman:这太厉害了,你能够招募到多少人去完成这个项目?
陶哲轩:50个左右 ,这在数学上被认为是一个巨大的数字。所以我们有一篇有50位作者的论文,还有一个大的附录说明每个人贡献了什么。
Q:在这种多人参与的项目中,有没有一种类似ELO评分的情况,可以根据贡献者的专业水平来为他们的贡献打分?
陶哲轩:这些精益项目的美妙之处在于,你可以自动获取所有这些数据,你知道,所有内容都必须上传到 GitHub,而 GitHub 会追踪谁贡献了什么。所以你可以在任何时间点生成统计数据,你可以说,哦,这个人贡献了这么多行代码或者其他什么的。但这些都是非常粗糙的指标,我不希望这会成为人们晋升评审的一部分。
不过我想在企业计算领域,人们已经在使用这些指标作为评估员工绩效的一部分了,再次强调,这是一个有点可怕的方向,会导致学术水平下降,我们不喜欢指标。
Lex Fridman:但学术界却在使用它们,只是使用的是旧指标,像论文数量。感觉这是一个有缺陷的指标,但也正朝着正确的方向发展,对吗?
陶哲轩:是的,我认为研究它很有趣,我们可以做研究来判断这些是否是更好的预测指标。有一个发现叫作古德哈特定律 (Goodhart’s law),如果一个统计数据实际上被用来激励表现,它就会变成一种游戏,而不再是一种有用的衡量标准。

因此,我们这个项目采用的是自我报告的形式。实际上,在科学领域存在关于人们贡献类型的标准分类,有概念、验证、资源提供、编程等等。有一个包含12个左右类别的标准列表,嗯,我们要求每位贡献者在一个包含所有类别所有作者的巨大矩阵中,在他们认为自己做出贡献的地方打勾,并且给出一个粗略的想法。比如你可能做了一些编程工作、提供了一些计算资源,但没有做任何纸笔验证或其他工作什么的……
传统上数学家们只是按姓氏的字母顺序排列,而我们没有这种传统,科学也有第一作者、第二作者的划分等等,我们也没有。我们为此感到骄傲,因为我们让所有作者拥有平等的地位。
但它也不能完全上升到这个高度。十年前我参加了一个一些被称为“多数学者项目”的事情,它是众包数学,那时候还没有Lean,所以它受限于需要一个主持人来检查所有提交的贡献是否真正有效,这实际上是一个巨大的瓶颈。嗯,我们仍然有一些项目有10位作者左右,但我们当时已经决定不要试图划分每个人做了什么,而是共同使用一个假名,因此我们以 Bwaki 的精神为基础,创造了一个名为DHJ Polymath的虚构人物,Bwaki是20世纪一群著名数学家的笔名。
当时的论文是以DHJ Polymath这个笔名来发表的,所以我们都没有获得作者署名。实际上这不算一个好结果,原因有几点,其中的一点是,如果你想要被考虑终身教职或者什么,你不能使用这篇论文作为你的出版物之一去提交,因为你没有正式的作者署名。另一件事情是,直到很久以后人们才意识到,当人们提到这些项目时,只会提到项目中参与的最著名的人,而不是其他参与者。
所以这次我们尝试了一些不同的:让每个人都有作者身份,同时附上这个矩阵来解释它如何运作。
Lex Fridman:仅仅是参与这样的大型合作项目就足够出色了。我看过几年前Kevin Buzzard关于 Lean 编程语言的一个演讲,你说这可能是数学的未来,这一点也很让人兴奋——世界最伟大的数学家之一也在拥抱这个似乎正在开创数学未来的东西。
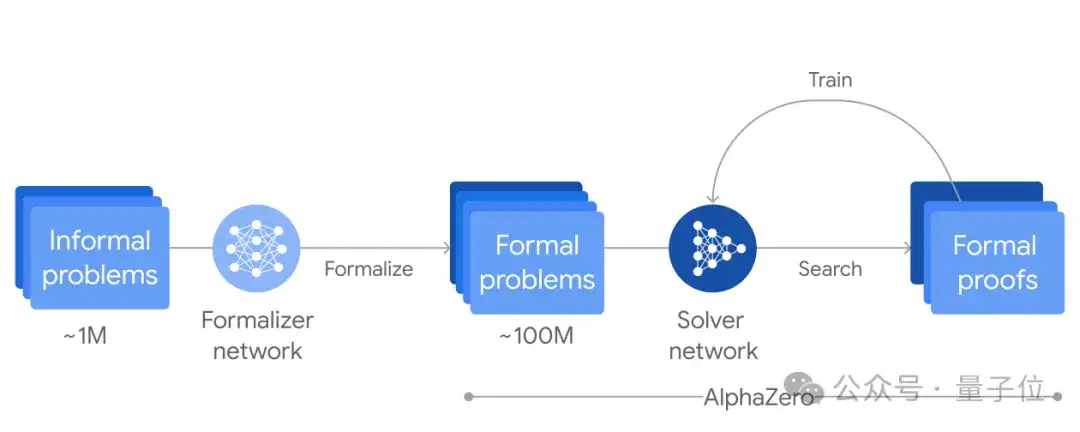
DeepMind的AlphaProof系统
Q:DeepMind的AlphaProof系统是通过强化学习训练的,使用的数据包括国际数学奥林匹克(IMO)问题在Lean中成功和失败的形式化证明,这属于较高水平的高中数学问题。这个系统怎么样?证明高中级别问题的系统与研究生级别问题之间存在着怎样的差距?
陶哲轩:随着证明中步骤数量的增加,难度会呈指数级增长,这是一次组合式爆炸。大型语言模型的问题在于它们会犯错误:如果一个证明有20个步骤,而你的模型在每个步骤中有10%的失败率去走向错误的方向,真正到达终点的可能性很小。
△图片来源于AlphaProof项目页
Lex Fridman:稍微扯一下题外话——从自然语言映射到形式程序的问题有多难?
陶哲轩:是的这实际上非常难,自然语言有很强的容错能力,你可以犯一些小的语法错误,第二语言的说话者还是能大致理解你在说什么;但是形式语言,如果你有一个小地方出错,整个事情就都成了无稽之谈。甚至形式到形式都非常困难,不同语言中存在不同的、互不相容的序言,有Lean、Coq和Isabelle等等,即使从形式语言转换到形式语言,依然是一个基本尚未解决的问题。
Lex Fridman:但是一旦你有了他们使用的非正式语言,他们就会用 RL 训练模型,用类似于AlphaZero的模型去尝试提出证据。他们还有一个模型,我相信是用于几何问题的独立模型。那么这个系统给你留下什么样的印象呢?你怎么看待这些差距?
陶哲轩:我们之前讨论过,随着时间的推移,一些令人惊叹的事情会变得有些常态化。当然,几何是一个可以解决的问题,这些都是很伟大的作品,展示了什么是可能的。但这个方法目前还不具备可扩展性,Google服务器时间要用三天时间去解决一道高中数学题。随着复杂性的指数级增加,这并不是一个可拓展的前景。
Lex Fridman:我们需要提一下他们获得了银牌。
陶哲轩:只是相当于银牌表现。首先,他们花费的时间远超规定时限,而且是在人类协助下完成形式化验证的。但既然解决方案获得了满分评定——我想这是因为通过了形式化验证——所以这种评判应该算是公平的。
事实上已经有人提议要举办一场”AI数学奥林匹克竞赛”。具体设想是:在人类选手参加正式奥林匹克竞赛的同时,AI系统也将同步获得相同的赛题,并在相同的时间限制内作答,所有解答结果都将由同一批评委进行评分。这意味着AI必须使用自然语言而不是形式化语言来完成证明。
但我希望下一届IMO比赛不会出现这种情况——这次IMO的表现确实在时间限制内不够理想。不过,在一些规模较小的竞赛中,比如那些只需要给出具体数字答案而非完整证明过程的比赛,AI的表现其实要好得多。因为对于这类有明确数值答案的问题,强化学习会更容易一些:你得到了正确答案、你得到了错误答案,这是非常明确的信号。
但长篇证明要么必须正式,这样Lean系统才能给出赞同或反对的反馈;要么就是非正式的,需要人类来评分。如果你试图进行数十亿次的强化学习运行,你知道,你无法雇佣足够多的人来对这些进行评分。实际上,光是基于常规文本进行强化学习对当前的语言模型来说已经很有挑战性了,而现在如果不仅要雇佣人工审核员给出好评或差评,还要对输出结果进行严格的数学验证……这样做的成本实在太高了。
“嗅觉”是人类特有的优势
Q:人类在数学领域最独特的能力是什么?哪些方面是AI短期内难以突破的?
陶哲轩:我认为数学家们所做的工作的性质随着时间的推移发生了很大的变化。
一千年前,数学家需要计算复活节的日期——那涉及极其复杂的运算,但这些计算早在一个世纪前就被自动化取代了。他们过去还要运用球面三角学进行航海导航,完成从旧大陆到新大陆的复杂计算,这些也都实现了自动化。
即使在AI出现之前,像Wolfram Alpha这样的工具(虽然它不是语言模型)已经能解决许多本科阶段的数学问题。在计算层面,验证常规问题——比如给出一个偏微分方程题目,要求AI用20种标准解法的其中一种求解——AI可以回答:”我已尝试全部20种方法,这里有100种不同的排列,这是我的结果。”这类任务AI将表现得非常出色。一旦你解决了其中一个问题,就可以让AI攻击100个相似的变体。
但人类仍然保有独特的优势:当前AI最大的短板在于,当它走错路时它可能会说:”我要把问题拆分为两种情况,尝试这个技巧。”对于简单问题,运气好时这个方法有效;但有时它提出的解题思路完全是胡说八道,即使看上去像模像样。这是语言模型生成数学内容很让人头疼的地方。
确实,人类撰写的低质量数学内容我们也见过不少,比如缺乏正规训练者的投稿。但糟糕的人类证明通常能快速识别,它会犯一些非常基本的错误;而AI生成的证明却可能表面完美无瑕,因为强化学习实际上就是训练它们去生成看起来像是正确的文本,这对许多应用场景来说这就已经够了。所以错误往往非常隐蔽,等你找到它们时,又会发现它们真的很愚蠢,因为没有人会真的犯这种错误。
Lex Fridman:是的,这在编程环境下非常令人沮丧,因为我自己也经常编程。当人类写低质量代码时,有一种叫做代码异味(code smell)的东西,你可以立刻看出来异常迹象。但AI生成的代码从表面看起来完美规范,直到最后你才发现其中隐藏着极其明显的愚蠢错误,偏偏这些错误还藏在看似良好的代码结构里。
陶哲轩:嗅觉是人类特有的一种东西,嗯,还有一种比喻性的数学嗅觉,但这个我们不清楚如何让 AI 复制它。Alpha Zero等程序在围棋和国际象棋等领域取得了一定的进展,在某种程度上,它们已经发展出了一种对围棋和国际象棋局势的嗅觉,它们知道这个局势对白方有利,对黑方有利。即使无法阐明原因,仅仅拥有这种“嗅觉”就让它们能够制定策略。
所以如果人工智能获得某种评估特定证明策略可行性的能力,你可以说:“我打算把这个问题分解成两个小子任务”,它们可以说:“嗯,这个看起来不错,这两个子任务看起来比你的主要任务更简单,而且它们仍然有很好的机会实现,值得一试。”或者“哦不,你让问题变得更糟糕了,因为这两个子问题实际上比你原本的问题还要难。”这种情况实际上经常发生,当你尝试一些随机的方法,很容易把问题变得更加复杂而不是变得简单。所以,如果AI能够拥有“嗅觉”,那它们也许可以开始和人类水平的数学家媲美。
Lex Fridman:这是一个难题,但不是竞争,而是合作。我们假设一下,如果我给你一个能够做到你某些方面的能力的预言机,你可以与之合作,你希望那个预言机能做什么?你是否会希望它成为一种验证器,去检查代码异味,就像你本人那样?陶教授,这是一个充满希望、富有成果的方向。或者你想让它生成可能的证明,然后由你来看哪一个是正确的?你喜欢的话,或许还可以生成不同的表现形式,用完全不同的方式去看待同一个问题?
陶哲轩:是的,我认为以上选项都有可能,很多时候我们不知道如何使用这些工具,因为这是一种范式。过去我们从未遇到过如此矛盾的AI系统——它们既能理解复杂指令并处理海量任务,又会在细微处表现出令人不安的不稳定性,同时却仍能产出相当优质的结果。这种既强大又不可靠的特性组合确实耐人寻味。
这就像同时具备了两种特质的混合体:一方面如同可以深入交流的研究助手,另一方面又像传统软件工具那样具备规模化运行能力,只不过前者无法规模化,后者又太过局限。Tim Gowers早在2000年就预见到了这种数学协作场景,说来有趣,距今正好二十多年。他在文章中设想了一个未来数学助手与人类数学家的对话场景:人类提出创意构想,AI负责评估可行性;AI也会主动建议”需要验证100个特例吗”;或是实时反馈”你说命题对所有n成立,但我发现n=46时出现反例”。这种自由流动的协作模式正是我们所期待的:人类和AI双方随机提出想法或计算需求,没有预设路径。
我测试过这种协作方式,故意用已知答案的问题与AI合作。但当我建议使用某种方法时,AI往往会另辟蹊径。有时它能发现精妙的论证思路,有时却会完全偏离正轨,这时就不得不打断:”不对不对,这个方向错了,使用这个方法。”好的,它可能就会开始使用我提出的方法,然后回到我们期望看到的路径。但你必须一直去引导它,才能让它走上你想要的路径,让它更像你,最终才能强迫它给出你想要的证明。
就像是要赶一只猫一样,嗯,我需要付出的个人努力,不仅在于引导它,还要去检查它的输出,因为它看上去能成功但实际上并不可以。这比自己做还要累得多,但这就是当前最先进的水平。
Lex Fridman:我想知道是否会发生一个阶段性的转变,以至于不再感觉像是在赶猫,也许它的发展速度会让我们感到惊讶。
陶哲轩:我相信会。在形式化方面,我之前提到过,形式化一个证明比用手写要花费 10 倍的时间。但用这些现代 AI 以及更好的工具,Lean的开发者们正在做得更加出色,他们不断增加更多功能并使其更用户友好,这个时间正在从9倍降到8倍再降到7倍……好的,这没什么大不了,但终有一天它会低于1。这就是一个阶段性的转变。
因为当你写论文的时候,它忽然就有意义了。先用Lean语言完成证明,或是通过与AI实时协作完成内容,这个流程将变得理所当然,而期刊审稿流程也将随之革新:对于已经通过Lean形式化验证的论文,审稿人只需要评估研究成果的重要性和它与现有文献的关联性,而不需要过度担心证明过程的正确性,因为这些都是已被系统认证过的。
数学领域的论文正在变得越来越长,实际上,除非它们非常重要,否则为那些真正长的论文找到好的审稿人越来越难。这确实是一个问题,而形式化恰好在合适的时间出现,使得这种情况变得更容易猜测。
Lex Fridman:随着工具链的完善和其他相关因素的发展,我们可以预见Mathlib这类数学知识库很可能呈现指数级增长,这是一种良性循环。
陶哲轩:是的,我的意思是,LaTeX 如今已成为所有数学家使用的标准排版语言。过去人们使用各种文字处理器和打字机,但在某个时间点,LaTeX比其他所有的竞争对手都更容易使用,短短几年内就完成了整个学术界的彻底转换,这种转变堪称戏剧性。
AI和菲尔兹奖的距离:差一个研究生
Q:距离 AI 系统作为合作者参与获得菲尔兹奖级别证明的研究,我们还有多少年?换句话说,AI 何时能达到这种顶尖协作水平?
陶哲轩:这取决于AI和人类协作的水平。
Lex Fridman:我的意思是,它是否值得获得菲尔兹奖。
陶哲轩:各占一半吧,如果这是一篇获奖论文,其中包含一些 AI 系统协助写作的话,你知道,就比如说,仅是完成顺序就已经…我使用它来加速我自己的写作。比如说,你可以有一个定理,有一个证明,证明分为三个情况,我写下第一个情况的证明,而自动补全建议:“现在,这里是第二个情况证明该如何进行”,并且它完全正确,太棒了,节省了我大约5到10分钟的打字时间。
Lex Fridman:但在那种情况下,AI系统并不会获得菲尔兹奖。我们是谈论20年、50年还是100年?你觉得呢?好吧。
陶哲轩:我曾经发表过一个预测,到2026年——也就是明年——将会出现AI和数学的合作,不是获得菲尔兹奖的那种,而是实际研究水平的数学,比如一些由 AI 部分生成的、已发表的想法。也可能不是想法本身,但至少是一些计算或者验证工作。
Lex Fridman:这种情况已经发生了吗?
陶哲轩:已经发生过了,是的。有些问题是通过复杂的流程解决的,即与 AI 对话来提出想法,然后人类去尝试,尽管它有可能不适用。
Lex Fridman:但它会提出一个不同的想法。
陶哲轩:确实有一些数学成果,只有在人类数学家和AI的共同参与下才得以完成,但他们的功劳很难理清。我的意思是,尽管这些AI工具并不能复制数学运算所需要的所有技能,但它们可以复制其中的相当一部分,大概30%到40%,它们可以填补某些方面的空白。
编程就是一个很好的例子:用Python编程对我来讲是一件很麻烦的事,毕竟我不是一个专业的程序员,但是AI大大降低了做这件事情的摩擦成本,它为我填补了这个空白。现在AI在文献综述方面已经做得相当不错了,但仍然存在一个幻觉的问题,你知道,有些时候它会给出一些完全不存在的参考文献。但我认为这是一个能够解决的问题,通过用正确的方式进行训练等等,或者可以使用互联网进行验证,在几年之内应该就可以到达这样的水平:当你需要一个引理时,你可以问AI,之前是否有人证明过这个引理?AI就会进行一次高级的网络搜索,然后告诉你,这里有6篇论文提到了类似的情况。
我的意思是你现在就可以问它,它会给你6篇论文,但其中可能只有一篇是真实且与问题相关的、一篇真实但与问题无关,剩下4篇完全是凭空捏造出来的。AI现在确实有非零的成功率,但存在太多的垃圾信息,信号与噪声的比率太差了,以至于它只有在你已经大致了解需要的关系时才最有帮助。嗯,你只需要被提示、被提醒一篇已经潜藏在你记忆中的论文,而不是帮助你发现那些你甚至没有意识到但却是正确引用的新内容。但是当它做到时,那个正确的选项会被埋没在其他一系列的糟糕选项中。
Lex Fridman:AI能够自动生成一个靠谱的相关工作部分是一件很美妙的事情,它可能会带来另一个阶段的变化,因为它能正确地归功于人,并帮人类跳出“是的”这个思维定式。
陶哲轩:现在有一个很大的障碍需要克服:这就像自动驾驶汽车,你知道,它的安全边际必须非常高才行。所以,是的,所有AI应用都存在“最后一公里”问题,它们可以开发出20%到80%的时间里都有效的工具,但这仍然不够,事实上,在某些方面甚至更加糟糕。
Lex Fridman:换个方式来问菲尔兹奖的问题,你认为在哪一天它会让你真正地感到惊讶?当你读到头条新闻关于AI做了某件事的报道,一种真正的突破,让人惊呼”这是菲尔兹奖级别”,就像当年AlphaZero在围棋领域的突破那样。
陶哲轩:大概是十年,我能看到它做出两个人们认为无关的事情之间的猜想,并且实际上很有可能正确并且有意义。目前的模型面临着很多困难,我的意思是,举个例子,物理学家梦想让AI发现新的物理学定律,你知道,他们的梦想就是你只管将所有的数据喂给AI,它就能够给出我们以前从未见过的新的规律。但实际上,目前的尖端技术甚至难以从数据里发现旧的物理规律,即使它发现了,也存在很严重的污染,也就是说它之所以能够做到,只是因为它已经在某个训练数据中得到了这个旧规律,比如说玻意耳定律,或者任何你试图重构的规律。
部分原因在于,我们并没有针对于此的正确类型的训练数据,对于物理定律来说,我们并没有一百万个不同的宇宙,每个宇宙包含一百万条自然定律。
虽然我们已经发表了很多人们能够证明的东西,以及最终被验证的猜想,或者产生的反例,但是我们没有关于那些被提出但很快被意识到是错误猜想的数据,然后人们说,哦,我们应该实际上改变我们的主张,以这种方式修改它,使其更具合理性。一个像这样的试错过程是人类数学发现中真正不可或缺的一部分,但我们不记录它,因为它很尴尬。
呃,我们会犯错,但我们只愿意发表我们的成功,所以人工智能没有办法访问这些数据来训练。我有时候开玩笑说,AI得去读个研究生,真的,你知道得去上研究生课程、做作业、去办公室、犯错,嗯,得到关于如何改正错误的建议并从中学习。
庞加莱猜想:想象一个被揉皱并扭曲的球
Q:Grigori Perelman在七年时间里几乎不与外界接触,独自解决了庞加莱猜想,这是个什么问题?也许再谈谈Grigori Perelman的这段经历?
陶哲轩:好的,这是一个关于弯曲空间的问题,地球就是一个很好的例子。你可以想象一个二维曲面,它可能是一个带洞的环面,也可能有很多洞,而且表面可能有多种先验拓扑结构,即使你假设它是有界的、光滑的等等。我们已经弄清楚了如何对曲面进行分类,初步近似地看,一切都由一种被称为亏格的属性决定,即这个曲面上有多少个洞:球体的亏格为0,环面的亏格为1,以此类推。
区分这些二维曲面的一种方法是,球体具有一种被称为单连通性的特性,意味着如果你在球体上取任何闭合环路,它都可以被收缩成一个点,同时保持在曲面上,而环面并不具备这种性质。如果你在一个环面的外部取一根绕着环面的绳索,它无法通过环面的那个洞,也就没有办法闭合并收缩成一个点。球体是唯一具有这种可收缩性性质的曲面,直到球面经过连续变形。这就是我想称之为与球面拓扑等价的物体。
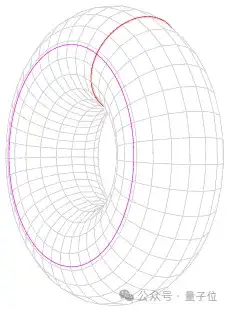
庞加莱在更高的维度上提出了相同的问题,但这变得难以可视化,因为你可以在三维空间中想象一个曲面,但作为一个弯曲的自由空间,我们对四维空间没有很好的直观理解,无法将三维空间嵌入到四维空间中,我们需要五个、六个甚至更高维度的空间。但无论如何,从数学上讲,你仍然可以提出这个问题:如果你有一个有界的三维空间,它还具有这个单连通的性质,即每一个闭合曲线都可以收缩,你能把它变成一个三维球体的版本吗?这就是庞加莱猜想。
奇怪的是,在四维、五维甚至更高维度上,这个问题反而更容易解决——它首先在更高的维度上得到了解决——可能是因为某种程度上,它有更多的空间来变形,更容易把事物变成一个球体。但三维情况下真的很难,人们尝试了多种方法,比如说某种剖分方法,把曲面分割成小三角形或四面体,然后根据这些面面如何相互作用来进行推导;或者也有代数方法,使用各种代数对象,比如所谓的“基本群”,你可以将它们附加到同调、上同调、以及所有这些非常高级的工具上。它们也没能完全奏效。
但是Richard Hamilton提出了一个微偏分方程(PDE)的方法,问题是这样的,你有一个球体,但它的呈现方式非常的奇怪:想象一个被揉皱并扭曲的球,让人看不出来那是个球。如果你有一个某种意义上是变形球体的曲面,你可以将它想象成一个气球,试着给它充气,随着空气的注入,它的皱纹会被抚平,就变成了一个漂亮的球体;但如果它是个环面或者类似的东西,它就会在某个点卡住。当内环收缩到零时,中间会得到一个奇点,并且无法再继续膨胀或者流动了。Richard Hamilton创造了这个流程,现在被称为里奇流(Ricci flow),这是一种把任意曲面或空间平滑化、变得越来越圆的方法,让它看起来像个球体。这个过程要么会形成一个球体,要么就产生一个奇点。就像是偏微分方程,它们要么具有全局规划性,要么就具有有限时间爆炸性,基本上这几乎是完全相同的事情。一切都是相互关联的。
Richard Hamilton指出,对于二维曲面,如果能保持永不形成奇点,就永远不会遇到麻烦,它会一直流动,并且形成一个球体,于是他得到了二维结果的一个新的证明。
Lex Fridman:这是一个很棒的解释,对于里奇流及其在此背景下的应用。对于2D情况来说,这里的数学有多难?
陶哲轩:这些是非常复杂的方程,与爱因斯坦方程不相上下,额,略微简单一些,但它们被认为是难以求解的非线性方程。2D中有很多特殊技巧可以提供帮助,但问题在于,在3D中这个方程实际上是超临界(supercritical )的。与纳维-斯托克斯方程相同的问题,随着爆发性增长,曲率可能会集中在越来越小的区域,并且看起来越来越非线性,情况变得越来越糟。
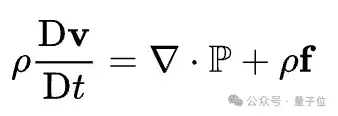
△纳维-斯托克斯方程的一般形式
可能会出现各种各样的奇点,其中一些可能存在于那些被称为“脖子夹”(neck pinchers)的、表面像杠铃一样的地方,并且在某一点收缩;有些奇点足够简单,你可以从中间剪开,然后就能把一个表面变成两个,并分别演化它们;但也存在这样的可能性:会出现一种非常棘手的像打了结一样的奇点,没办法对它进行任何“手术”。所以就需要对所有的奇点进行分类,比如知道事情可能会出错的所有方法是什么。
Perelman首先做的是把问题从超临界问题过渡到临界问题,像我之前说过能源的发明,哈密顿量阐明了牛顿力学。他介绍了一些概念,现在称为佩雷尔曼减少体积(Perelman’s reduced volume)以及佩雷尔曼的熵(Perelman’s entropy),并引入了新的量,比如能量,这些量在每个尺度上都保持一致。非线性实际上突然看起来不再像以前那么可怕了。

△Grisha Perelman证明庞加莱猜想的论文
他仍然需要分析奇点这一关键问题——这本身也是一个类似的问题——就难度上,和我所研究的波映射问题相当。所以Perelman设法对所有奇点进行了分类,并展示如何对每种情况进行处理。通过这种方式,他解决了庞加莱猜想。这包含了很多雄心勃勃的举措,今天的大语言模型都没办法做到。我的意思是,我充其量只能想象一个模型会将这个想法在数百种尝试方案中提出,但除此之外的99个将会是彻底的死路一条,而你只有在经过几个月的工作之后才能发现。Perelman肯定感觉到这是正确的道路才会去追求,因为从A到B要花费好几年的时间。
Lex Fridman:严格从数学角度来说,或者更广泛地,从流程上来说,你也做过类似困难的事情。你能从Perelman经历的过程中推断出什么?因为他是独自一人去完成这件事的。在这样的过程中会遇到哪些低谷?就像人工智能不知道自己什么时候会失败一样,当你坐在办公室里,意识到过去的几天甚至几周所做的事情是个失败的时候,你会作何反应?
陶哲轩:嗯,对我来说,我会换个问题。就像我说的,我是一只狐狸而不是一只刺猬。
Lex Fridman:但这是合理的,你可以休息一下,离开,去研究不同的问题。
陶哲轩:是的,你也可以修改这个问题,我的意思是,你可以去“作弊”,如果有什么东西阻碍了你,一些不好的情况不断出现,你的工具不起作用什么的……你可以假设按理来讲这种糟糕的情况不会发生,进行一些神奇的思考,从战略上来讲看看其它的论点是否成立。如果你的方法存在多个问题,那么你有可能就会放弃,但如果这是唯一的问题,其他的一切都顺利的话——那么它仍然值得挑战,你可以进行一些前方侦查什么的。
有时候犯错误甚至是有益的,我有一个项目确实因此赢得了一些奖项。和其他四个人一起,我们再次研究了这个PDE问题,实际上这又是一个爆破正则的问题,这种问题被认为非常困难。另一位菲尔兹奖得主Jean Bourgain曾经研究过这种问题的特殊情况,但他没能解决一般情况,而我们研究这个问题两个月,以为我们解决了它。我们作出了一个可爱的论证认为一切都吻合,为此我们很兴奋,我们计划举行庆祝活动,让大家聚在一起喝点香槟什么的。我们开始写它,然后我们中的其中一个人——不是我——另一位合著者说:“哦!在这个引理中,我们必须估算这个展开式中出现的13项,我们估算了其中的12项,但我们的笔记里却找不到第13项,有人能找到它吗?”然后我说:“好的,我会看看这个。”结果,好吧,我们完全忽略了这一项,并且这一项变得更糟糕了,比其他12项加起来还要糟糕。
事实上,我们没办法估算这个第13项,我们又尝试了几个月,尝试了几乎所有不同的排列组合,总有一个东西让我们无法控制。这非常让人沮丧。但因为我们已经投入了好几个月,并为此付出了好几个月的努力,我们依然在坚持。我们尝试了越来越绝望的、疯狂的事情,两年以后,我们找到了另外的一种方法,和我们最初的设想有些不同,这种方法并没有产生这些有问题的项,而是确实解决了这个问题。所以我们用了两年的时间解决了这个问题。但如果我们没有那个看似即将解决问题的虚假希望,我们可能在第二个月左右就放弃,并着手去解决一个更简单的问题了。如果我们知道要用2年的时间,我也不确定我们还会不会启动这个项目。
有时候这些不正确的——就像哥伦布在新大陆航行一样——这是一个测量地球大小的错误版本,他以为他会找到一条通往印度的新的贸易曲线,至少他在招股说明书上是这样宣传的,我的意思是,它实际上可能对此心知肚明。
Q:仅从心理因素来看,你有没有产生过最让你感到无措的自我怀疑?
Lex Fridman:感觉数学实在是太令人着迷了,当你在某个问题上投入太多精力但结果却是错误的时候,它可能会击溃你。就像是,国际象棋也击溃了一些人。
陶哲轩:我认为不同的数学家对数学有着不同的情感投入程度,有些人认为这只是个工作,你遇到了问题,你可以不解决,而是继续下一个,所以你总是可以继续投入另一个问题,这减少了情感上的联系。还有一些情况会产生一些被称为数学病的问题,就是他们会只抓住那个问题不放,花费数年只思考那个问题,即使他们的职业生涯会因此受损。但他们说:“好吧,但这是个大突破,一旦我解决了这个问题,它将弥补所有失去机会的岁月。”这种心态偶尔确实有效,但我讲真不推荐给没有毅力的人。
我从来没有对任何一个问题投入过多精力,一个帮助我们的点是,我们不需要提前明确我们的问题。当我们提交研究提案时,我们会说我们将研究这一系列问题,但即使我们不确定五年内我肯定会提供所有这些问题的证明,而是承诺取得一些进展或发现一些有趣的现象。也许你没能解决那个问题,但你发现了一个相关的、你可以对其说些新东西的问题,而那是一个更可行的任务。
加法和乘法都简单,但是合在一起……
Q:有没有一个一直困扰着你们的问题?像孪生素数猜想、黎曼猜想、克拉兹猜想?
陶哲轩:孪生素数,听起来……好吧,再说,我的意思是,像黎曼猜想一样,那真是遥不可及,甚至完全没有可行的途径。即使我使用了所有我知道的作弊手段,在这个问题里也依然无法从A到B。我认为首先需要在数学的其他领域取得突破,然后有人要认识到那个突破是可以运用于这个问题的。
Lex Fridman:所以我们应该后退一步,只讨论素数。它们通常被称为数学的原子。你能谈谈这些原子提供的结构吗?

陶哲轩:自然数有两种基本运算:加法和乘法。所以如果你想生成自然数,你可以做两件事之一:你可以从1开始,一次次地加1,这样就生成了自然数,所以从加法角度看,它们很容易生成1、2、3、4、5;或者你可以取质数,如果你想从乘法角度生成,你可以取所有质数,2、3、5、7,然后把它们全部乘在一起。这样你就得到可能除了1以外所有自然数。所以从加法和乘法角度看,自然数有两种不同的思考方式。单独来看,它们都不算太难,关于自然数的任何问题,如果是只涉及加法或乘法的,都相对容易解决。
令人沮丧的是,当你把这两者结合起来,问题忽然就变得极其丰富……我的意思是,我们知道数论中有一些命题实际上是不可判定的。像是某些多元多项式方程是否存在自然数解的问题,它们的答案取决于数学基础命题的不可判定性——比如数学公理本身的一致性。
但即使是最简单的问题,把一些乘法和加法运算结合起来,比如在素数上做一些附加操作,像是移动2位。分别来说我们都很了解,但如果你问当你平移一个素数两位时,能否得到一个另素数?或者你能多久得到另一个素数?将两者联系起来竟然变得如此困难。
Lex Fridman:孪生素数猜想就是这样的,它假设存在无限多对相差为2的素数。有趣的是,你在回答这些种类繁多的复杂问题时取得了非常成功的进展,比如你提到的格林-陶定理,它证明了素数序列包含任意长的等差数列。你能证明出这样的定理,真是令人难以置信。

陶哲轩:是的。所以我们意识到,这种类型研究的重点是不同的模式具有不同级别的不可摧毁性。孪生素数问题的难点在于,如果你把世界上所有的素数都列出来,3、5、7、11 等等,其中有一些是成对的,比如 11 和 13 是一对孪生素数,还有其他孪生素数等等。如果你愿意的话,你可以轻松地编辑素数以摆脱这些孪生素数。虽然孪生素数是无穷多的,但它们在素数里实际上相当稀疏,一开始确实有不少,但一旦到了数百万、数万亿级别,它们就变得越来越稀少。实际上,如果有人能够访问素数数据库,他们只需在这里或那里删除几个素数,就可以让孪生素数猜想成为错误。只需要删除0.01%的素数或者类似的什么,真是明智之举。
因此,你可以提供一个经过审查的素数数据库,它通过所有关于素数的统计测试、遵循多项式定理和其他质数效应,但不再包含任何孪生素数。这对于孪生素数猜想来说是一个真正的障碍,意味着任何旨在在实际素数中找到孪生素数的证明策略,在应用于这些稍作修改的素数时都必须失败。因此,这必定是素数中某种非常微妙、精细的特征,而不仅仅是通过整体统计分析就能得到的。
另一方面,算术级数被证明要稳健得多。你可以取素数,实际上可以排除 99%的素数,你可以选择任意90个参与者。结果发现,我们另一个证明是,你仍然可以得到算术级数。算术级数非常多,它们就像蟑螂一样。
Lex Fridman:对于不了解的人来说,算术级数是一系列相差某个固定值的数。
陶哲轩:是的。但它又像是那种无限猴子现象(一只猴子在无限时间内随机独立地敲击打字机键盘上的按键,几乎肯定会打出任何给定的文本),对于任何固定长度的集合,你不会得到任意长度的进展,只会得到相当短的进展。
Lex Fridman:但你说孪生素数不是无限猴子现象。我的意思是,这是一只非常狡猾的猴子,但它仍然是一种无限猴子现象。
陶哲轩:如果素数真的是随机的,这些素数是由猴子生成的,那么事实上无限猴子定理就是这样的。
Lex Fridman:但你说是孪生素数,你不能使用同样的工具。它看起来几乎不是随机的。
陶哲轩:嗯,我们不知道。我们相信素数的表现像是一个随机集合。所以我们关心孪生素数猜想的原因,是一个测试案例,测试我们是否能够真正地、自信地、假设错误率为0%,说素数表现得像是一个随机集合。我们已知的素数的随机版本至少有100%的概率包含孪生素数,或者随着你越来越向外延伸,概率趋于 100%。所以,我们相信素数是随机的。算术级数之所以不可摧毁,是因为无论它看起来是随机的还是周期性的结构,在这两种情况下,算术级数都会出现,但原因不同。这就是这个定理的基本原理,有很多证据都证明了算术级数定理,它们都通过某种二分法得到证明:即你的集合要么是结构化的,要么是随机的,在两种情况下你都可以说些什么,然后你把两者结合起来。
但在孪生素数中,如果素数是随机的,那么你很高兴,你就赢了。如果素数是结构化的,它们能够以一种特定的方式结构化并消除孪生素数。我们不能排除这个阴谋。
Lex Fridman:但据我了解,你可以做到在K元组(K-tuple)版本上取得进展。
陶哲轩:是的。所以关于阴谋的一个有趣之处是,任何一个阴谋理论都很难被证伪。如果你相信世界是由蜥蜴统治的,你会说“那么这里有一些证据表明它不是由蜥蜴统治的。”嗯,但是那个证据也是蜥蜴的阴谋,你可能遇到过这种情况。几乎没有办法可以明确排除阴谋,在数学上也是如此,一个完全致力于消除孪生素数的阴谋还必须渗透到数学的其他领域,但至少据我们所知,它可以保持一致。但有一个奇怪的现象,你可以用一个阴谋排除其他阴谋。所以如果世界是由蜥蜴统治的,它就不能同时是由外星人统治的,对吧?
所以一个不合理的事情很难被证伪,但多个不合理的事情就有工具了。比如我们知道存在无限多个素数,其中任意两个素数的差值不超过……实际上,这个数字最高是246,存在一个界限。所以有孪生素数;有一种东西叫做表亲素数(cousin primes),它们的差值为4;还有相差6的性感素数(sexy primes)——这个概念远没有其名称所暗示的那么令人兴奋。
你可以排除其中一个阴谋,可一旦你有 50 个阴谋,事实证明,你无法一次性排除所有的可能性。这需要这个阴谋空间里太多的能量。
Q:你是怎么做界限部分的?你是怎么为不同的素数发展界限的?
陶哲轩:所以这最终是基于一个被称为鸽巢原理(the pigeonhole principle)的东西。鸽巢原理就是,如果你有若干只鸽子,并且它们都必须进入鸽巢,而鸽子数量多于鸽巢数量,那么至少有一个鸽巢里必须有至少两只鸽子。所以必定有两只鸽子彼此距离很近。比如,如果你有 100 个数字,它们都介于 1 到 1000 之间,那么其中两个数字之间的距离最多为 10,因为你可以将 1 到 100 的数字分成 100 个鸽巢。假设你有 101 个数字,那么这 101 个数字中必定有两个数字之间的距离小于 10,因为这两个数字必须属于同一个鸽巢。这是数学基本原理的基本特征。
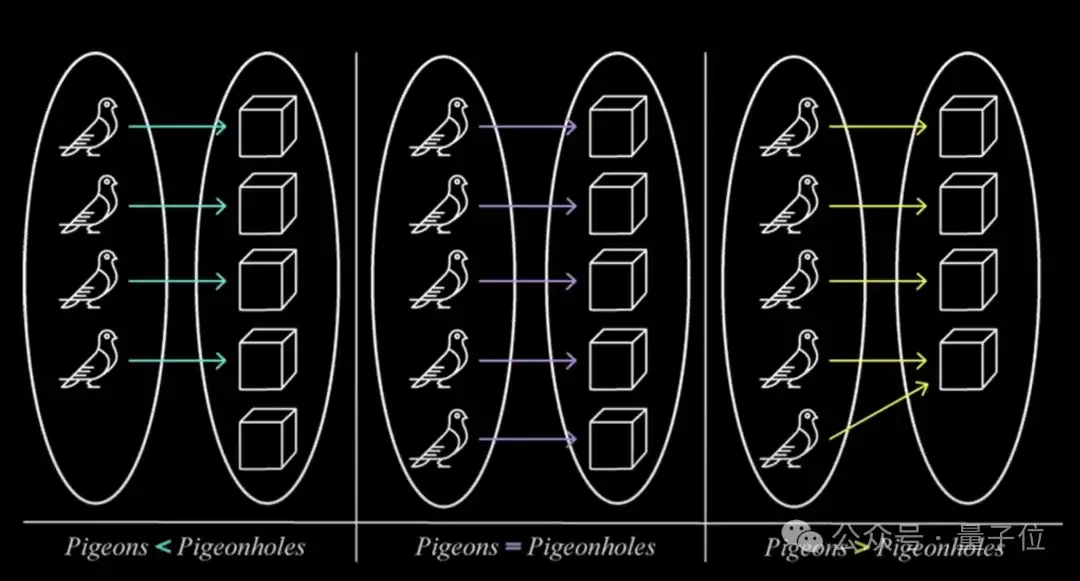
鸽巢原理不能直接和素数一起使用,因为素数在向外延伸时会变得越来越稀疏,也就是说质数会变得越来越少。但事实证明,有一种方法可以给数字分配权重。有些数字算是准素数(almost primes ),但它们并非没有除了自身和1以外的任何其他因数,只不过它们拥有的因数非常少。事实证明,我们对准素数比素数理解得更透彻。例如人们很早就知道存在孪生素数,这个问题已经被研究透了。所以准素数是我们能够理解的东西。因此,你实际上可以将注意力集中在合适的准素数集合上。素数相对来讲非常稀疏,相比之下,准素数的稀疏程度要低得多。
你可以构建一个准素数的集合,其中素数的密度大约是 1%,这能让你有机会通过应用某种鸽巢原理来证明大约只有100个素数。但为了证明孪生素数猜想,你需要获得素数的密度,在准素数内几乎达到50%的阈值,一旦达到 50%,你就会得到孪生素数。但不幸的是,无论你选择多么好的准素数集合,素数的密度永远不会超过 50%,这就是所谓的“奇偶性壁垒”(the parity barrier)。我非常想攻克它,所以,我长远的梦想之一是就找到一种方法来突破这个障碍,因为这将不仅解开孪生素数猜想,还能解开克拉兹猜想,和许多数论领域正在受阻的其它问题。因为我们的现有技术需要超越这个理论上的“奇偶性壁垒”,就像试图超光速行驶一样。
Lex Fridman:所以我们应该说孪生素数猜想是数学史上最大的问题之一,克拉兹猜想也是,它们感觉像是邻居。有没有哪天你觉得自己看到了解法?
陶哲轩:有的。有时你尝试某种方法,它就会非常有效,你就会感受到像我们之前谈到的数学气味(mathematical smell)。当事情进展顺利时,你会从经验中学习,因为有一些困难是不得不去遭遇的。我的一位同事可能会这样表达:如果你在纽约街头被蒙上眼睛放进车里,在几个小时后,你的眼罩被摘掉,发现你到了北京。我的意思是,这有点太容易了,不知道为什么并没有跨越海洋,即使你不知道具体发生了什么,你会怀疑有些事情不对劲。
Lex Fridman:但这仍然在你脑海中,你是否每次都会回到素数领域看一会儿?
陶哲轩:是的,在我没什么其他事情可做的时候——这种情况越来越少了,我现在有很多事情要处理——但当我有空闲时间,又不想做我的实际研究项目,也不想处理行政事务,或者不想为家人做些差事,我可以玩这些有趣的东西。通常情况下什么也得不到,你必须学会说:“好吧,再试一次,什么都没发生,我会继续前进。”偶尔我也会解决这些问题,或者有时就像你说的,你以为你解决了问题,然后你继续研究可能 15 分钟,然后你想到,“我应该检查一下,这简单得有点令人难以置信了。”通常都是这样。
Lex Fridman:关于孪生素数和克拉兹猜想这些问题的解决时间,你的直觉是怎么看的?
陶哲轩:关于孪生素数,我认为我们将会不断获得更多进展。这确实至少需要10年,这个“奇偶性壁垒”是剩下的最大的难题,有更简单的版本,我们已经非常接近这个猜想了。所以我认为在 10 年内我们将会有更多更接近的结果,但可能不会得到全部。孪生素数问题相对接近,但黎曼猜想,我一点头绪也没有,我的意思是,我想这是偶然发生的。
Lex Fridman:所以黎曼猜想是关于素数分布的更普遍的猜想,是吧?
陶哲轩:是的。这表明,在某种程度上只从乘性角度来看,对于只涉及乘法不涉及加法的问题,质数确实表现得像你希望的那样随机。
概率中存在一个现象称为平方根抵消(square root cancellation),如果你想要调查美国民众对某个问题的看法,并且只询问一两个选民,你可能会抽到一个糟糕的样本,然后你会得到一个对整体平均值的非常不精确的测量。但如果你抽样的人数越来越多,准确性就会越来越好,并且准确性随着你抽样人数的平方根而提高。如果你抽样 1,000 人,你可以得到 2%或 3%的误差范围。在同样的意义上,如果你以某种乘法性方式测量质数,你可以测量某种类型的统计数据,它被称为黎曼zeta函数,并且上下波动。
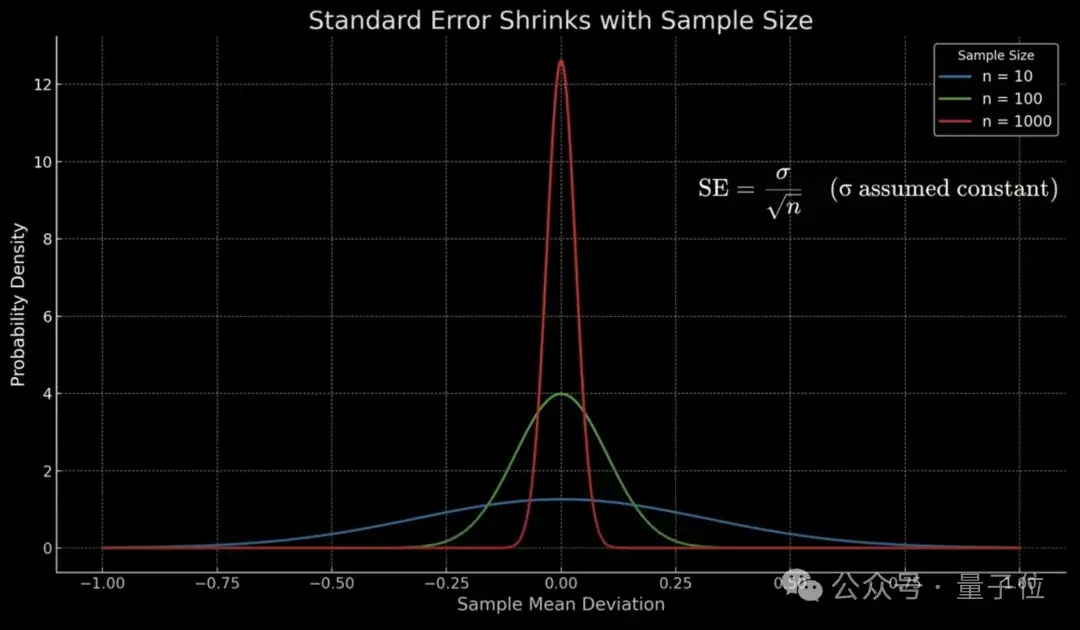
但从某种意义上说,随着你不断取更多平均值、不断进行更多采样,波动应该会像随机变量一样减小。并且有一种非常精确的方法来量化这一点。
黎曼猜想以一种非常优雅的方式捕捉了这一点,但就像数学中的许多其他方法一样,我们几乎没有工具来证明某件事真的表现得非常随机。这实际上不仅仅是一点点随机,但这种平方根抵消要求其行为像一个真正随机的集合一样随机。我们知道,对于与奇偶性校验问题有关的事情,大多数的常用技术都无法解决。证明必须出乎意料,但没有人提出过任何严肃的提议。正如我所说,有很多种方法可以解决,你可以稍微修改一下质数,就可以破坏黎曼猜想。它必须非常精细、你不能应用具有巨大误差范围的东西、它必须能够勉强工作,所有的这些陷阱你都会遇到并且非常娴熟地躲避。
Q:对你来说,素数最神秘的是什么?
陶哲轩:这是个好问题,从推测上来说,我们对素数有一个很好的模型。我的意思是它们具有某些规律,比如质数通常是奇数。但除了存在一些明显的规律外,它们表现得非常随机,只是假设它们会这样表现。
所以有一个称为 Cramér质数随机模型的东西,在某个时间点之后,素数的表现就像一个随机集合。这个模型还有各种细微的修改,但这是一个非常好的模型,它与数值相匹配,并告诉我们应该预测什么。就像是我告诉你可以完全肯定孪生素数猜想是正确的。随机模型给出了极高的准确性,我只是无法证明这一点。我们的数学大多是为了解决包含规律的问题而优化的。而质数存在这种反模式,实际上几乎所有事物都是这样,但我们无法证明这一点。
我想质数是随机的并不神秘,因为它们没有必要有任何秘密模式。但神秘的是,究竟是什么机制真正迫使随机性发生?这一点完全缺失。
克拉兹猜想:赌桌上没有赢家
Q: 克拉兹猜想陈述简单而富有美感,解决起来却极其困难。Paul Erdos关于克拉兹猜想说过,数学可能还没有准备好解决这类问题。还有人表示这是一个极其困难的问题,完全超出了当前数学的范畴——这是在 2010 年的说法,但你已经取得了一些进展。为什么如此难以解决?你能解释一下它到底是什么吗?
陶哲轩:这是一个可以解释的问题,借助一些视觉辅助工具会更有帮助。你可以取任何一个自然数,比如 13,然后对它应用以下步骤:如果它是偶数,就除以2,如果是奇数,就乘以3再加1。这样做,偶数会变小,奇数会变大,所以13会变成40,因为13乘以3是39,加1就得到40。这是一个简单的过程。对于奇数和偶数,它们都是非常容易的操作。然后把它们结合起来,仍然相当简单。

但接着你会问,迭代它会发生什么?把刚刚得到的输出反馈回去,所以13变成40,40现在是偶数,除以2是20;20仍然是偶数,除以2是10,5;然后5乘以3加1是16;然后是8,4,2,1;然后从1开始,它会变成1,4,2,1,1,4,2,1,无限循环。
所以,我刚才描述的这个序列,13,40,20,10,这些都是所谓的冰雹序列,有一个关于冰雹形成的过于简化的模型,这个模型实际上并不完全正确,但仍然以初步近似的身份被教给高中生。这个模型是:一个小冰块形成冰晶并悬浮在云中,因为风的作用上下移动,有时在寒冷时它会获得一些质量,也许也会稍微融化一点。这个上下移动的过程形成了部分融化的冰,最终导致冰雹的形成,然后它最终会落到地球上。
克拉兹猜想是,无论你从多高的地方开始,你取一个数,这个数可能是数百万或数十亿,这个上下移动的过程,如果你是奇数就上升,是偶数就下降,它最终总会落到地球上。
Lex Fridman:也就是说无论你从这个非常简单的算法的哪里开始,你最终都会到达1。
陶哲轩:如果你绘制这些序列,它们看起来像布朗运动、像股票市场。它们似乎以看似随机的模式上下波动。事实上通常就是这样,如果你输入一个随机数,实际上可以证明,至少在最初,它看起来像随机游走。而这是一个向下漂移的随机游走。就像如果你总是在赌场玩轮盘赌,而赌注稍微对你不利。所以有时你赢,有时你输,但在长期来看,你输的比赢的多。通常如果你一遍又一遍地玩,你的钱包会变成零。
我证明的结果大致是,从统计上看,大约99%的输入会漂移到——可能不是完全到1——但会比开始时小得多。所以这就像我告诉你,如果你去赌场,大多数情况下,如果你玩得足够长,你最终手里的钱会比你开始时少。这有点像我证明的结果。
Lex Fridman:你能沿着这个思路继续证明完整的猜想吗?
陶哲轩:嗯,问题在于我使用了概率论中的参数,并且总有这种特殊事件发生。在概率论中,我们有这个大数定律,它告诉你例如如果你在一个赌场玩一个期望值随时间递减的游戏,你几乎可以肯定以接近100%的概率会输钱,但总会有一些例外情况。从数学上讲,即使游戏的概率并不有利,你也可能只是稍微比输的次数多赢几次。
这和Navier-Stokes方程非常相似,大多数时候你的波可以分散,但可能存在一个例外性的初始条件选择,会导致你“爆炸”。而且可能存在一个例外性的特殊数字选择,它们被放入其中会飞向无穷大,而所有其他数字会坠入地球,坠入一个点。
事实上,有一些数学家,比如Alex Kontorovich提出,这些坍缩迭代实际上类似于细胞自动机。实际上,如果你看它们在二进制中的表现,它们确实有点像生命游戏类型的模式。类比于生命游戏如何创造出巨大的自我复制物体等等,或许你可以创造出某种比空气重的飞行器。一个编码这种机器的数字,它的任务就是编码,创造出某种更大的版本。
Conway也研究了这个问题,实际上非常相似,那对Navier-Stokes项目更具有启发性。Conway研究了克拉兹问题的推广,其中不是乘以三加一或除以二,而是有更复杂的分支列表,而不是两种情况。也许有17种上下波动的情况,他展示了一旦你的迭代变得足够复杂,你实际上可以编码图灵机,并且可以让这些问题变得不可判定。事实上,他发明了一种编程语言,用于这类分式线性变换,他称之为FractRat。这是一个关于“Fortran”的文字游戏。你也可以进行编程,如果你输入的数字被编码为素数,它就会降为零,否则就会上升,诸如此类。这类问题的总体复杂性实际上与所有数学一样复杂。
Lex Fridman:我们之前讨论过的细胞自动机的一些神秘之处,有一个数学框架来谈论细胞自动机,也许在克拉兹猜想中也需要同类型的框架。
陶哲轩:如果你要做——不是统计上,而是你真的想要去做——地球上所有输入的100%,可行的可能是统计学上的99%,趋近于1。但就像所有事情一样,那看起来很难。
找到P=NP的算法,可以同时解决很多其他问题
Q:在所有著名的问题中,你觉得哪个在可触及范围内是最难的问题?是黎曼猜想吗?
陶哲轩:黎曼就在那里。P =NP是个好问题,因为它是个元问题(meta problem)。如果你解决了这个问题,从积极的意义上来说,找到了P等于NP的算法,那么这有可能同时解决很多其他问题。
Lex Fridman:我们应该提到一些我们一直在谈论的猜想,现在很多内容都是建立在它们之上的。P=NP的连锁反应比其他任何的都多。
陶哲轩:如果黎曼猜想被证伪,那将给数论学家带来巨大的精神冲击,但它也会对密码学产生连锁效应,因为很多密码学都使用数论,使用涉及质数等的数论构造。它非常依赖于数论学家多年来积累的直觉,其中涉及质数的运算哪些是随机的,哪些不是。特别是,加密方法被设计成将文本信息转换成看似随机噪声的文本,因此我们相信,至少在数学上,几乎不可能被破解。但如果某个东西动摇了我们的信念,就像黎曼猜想是错误的,这意味着存在我们尚未知晓的质数实际模式。有一种就会有更多,我们的许多密码系统都会因此受到质疑。
Lex Fridman:但那样的话,你又如何去谈论质数呢?又走向克拉兹猜想了,你希望它是随机的对吗?
陶哲轩:是的,所以更广泛地说,我只是在寻找更多工具、更多方法来证明事物是随机的。如何证明阴谋没有发生?
Q:在你看来,P=NP这种事情是可能发生的吗?你能想象一个它发生的宇宙吗?
陶哲轩:这是可能的。我的意思是,存在各种情况。有一种情况是它在技术可行的,但实际上不可实施。证据有点倾向于否定,即P可能不等于NP 。
Lex Fridman:我的意思是,这看起来像是类似于黎曼猜想的那种情况。我认为证据非常倾向于否定。
陶哲轩:是这样,倾向于否定远比倾向于肯定要多。关于P=NP的有趣之处正在于,我们面临的障碍也比几乎所有其他问题都要多。所以虽然有一些证据,但我们也有很多结果排除了许多种解题方法。这是计算机科学实际上做得非常出色的一件事:它确实表明某些方法行不通。
突然,人们开始想要知道你的意见
Lex Fridman:我读过一个有趣的故事,说当你获得菲尔兹奖时,有个人从互联网上给你写信,问你在获得这个崇高奖项后打算做什么?然后你很快就非常谦逊地回答说,闪亮的金属并不能解决我目前正在研究的问题,所以我会继续研究它们。
首先,我觉得你在那种情况下回复邮件很有趣,其次,这也显示了你的谦逊。但无论如何,也许你可以谈谈菲尔兹奖,但这也是我询问Gregorio Perlman的另一种方式。你认为他为什么会以拒绝菲尔兹奖和随之而来的价值 100 万美元的千禧年奖而闻名?他声称:“我对金钱或名声不感兴趣。这个奖项对我完全无关紧要。如果证明是正确的,那么其他任何认可都不需要。”
陶哲轩:Perlman甚至在那些倾向于有些理想主义观点的数学家中也算是个异类。我从未见过他,我想有一天见到他会很有意思,但我从未有过这个机会。我认识见过他的人:他总是对某些事情持有强烈的观点。我的意思是,他并不是完全脱离数学界,他会发表演讲、写论文等等,但在某个时刻他决定不再和社区的其他人打交道了。
他有些失望或是什么,我不知道,他决定离开,去圣彼得堡采蘑菇或是别的什么。那也可以,你可以那样做。那是事情的另外一面。我们解决的很多问题中,有些确实能够实际应用,那很棒。但如果你停止思考某个问题……所以他自那以后在这个领域没有再发表过论文,但这没关系,还有许多、许多其他人也这样做了。
所以我想,我最初没有意识到菲尔兹奖有点让你成为体制的一部分。大多数数学家,职业数学家,只是专注于发表下一篇论文,也许提升一个等级,开始几个项目,可能带了一些学生之类。但突然人们开始想要知道你的意见,你必须稍微思考一下那些你可能会愚蠢地说出来的话,在过去没有人会听你的,现在这更重要。
Q:菲尔兹奖对你有束缚感吗?你还能像以前一样享受乐趣、保持叛逆精神、尝试疯狂的事情、玩弄想法吗?
陶哲轩:我现在的空闲比以前少了很多,这主要是我的选择。我的意思是,我总可以选择拒绝,所以我拒绝了很多事情。我还可以拒绝得更多,或许我的声誉会变得不那么可靠,以至于人们不再向我询问。这总是一个选择。
但我作为博士后,并没有像我现在这样花那么多时间只专注于一个问题,或者瞎搞。我仍然会做一点。但是,随着你在职业生涯中不断进步,软技能(soft skills)变得越来越重要,数学在某种程度上把所有技术技能都提前到职业生涯的早期阶段。所以作为博士后,你要么发表成果,要么被淘汰。你被激励于基本上专注去证明非常技术性的定理,这样既能证明自己,也能证明算法,但是,当你职位更高时,你必须开始指导学生、面试,并试图塑造领域的研究方向,有时你还得处理各种行政事务。这是一种适当的社会契约,因为你需要深入工作,看看什么能帮助数学家。
Lex Fridman:另一方面,建立秩序的真正积极之处在于,你可以成为照亮许多年轻数学家或对数学感兴趣的年轻人的光。我可能会说,我挺喜欢菲尔兹奖的,它在某种程度上激励了很多年轻人,这就是人类大脑的运作方式。同时我也想向Perlman这样的批评奖项的人表示敬意,在他看来,那是他的原则,任何能够按照自己的原则行事、做到大多数人都做不到的事情的人,看到这一点都令人赞叹。
陶哲轩: 一定程度的认可是有必要的,也很重要,但同样重要的是不要让这些事情主宰你的生活,只关注获得下一个大奖之类的。所以你会再次看到这些试图只解决重大数学问题,而不去处理那些不那么“吸引人”,但确实有趣且富有启发性的事情的人。
正如你所说的,就像人类思维的工作方式一样,当我们理解的事物与人类相关联,并且与少数人类相关联时,我们会更好地理解。以我们人类思维的构造方式,我们能理解 10 到 20 个人之间的关系,但一旦超过 100 个人——我想有一个专有名称来描述这种限制,超过这个限制,它就变成了“盲众”。所以我们必须简化整个群体,你知道,99.99%的人类都变成了“盲众”,这些模型往往是不正确的,这会导致各种问题。
所以是的,为了让一个学科更人性化,如果你识别出少数几个人,并说这些人代表了这个学科,比如榜样,这确实有一定的作用。但它也可能有害,因为我会第一个说,我自己的职业道路并不是典型的数学家的道路。
那种非常加速的教育,我错过了很多课,我认为我一直有非常幸运的指导机会,我处在正确的时间、正确的地点。某人的轨迹和我不同并不意味着他们不能成为优秀的数学家,他们会成为,但风格会非常不同,而且我们需要不同风格的人。
有时人们过于关注完成数学或其他领域耗时数百年或数十年的项目中的最后一步,而忽略了这一过程建立在大量先前工作之上。但如果你不是专家,很难讲述这个故事。简单地说某个人做了某件事要容易得多,历史也因此变得简单很多。
Lex Fridman:我认为总的来说,这是一件非常积极的事情。谈到乔布斯,作为苹果的代表,大家都知道——那令人难以置信的设计、令人难以置信的工程团队、团队中的那些个人。他们不是团队,而是团队中的个人,那个团队有很多才华,但这只是一个简洁的说法,就像乔布斯。
陶哲轩:是的,作为一个起点,作为一个初步的近似。
Lex Fridman:然后读一些传记,去了解更深的初步近似。
我们需要那些有毅力和无畏精神的人
Q:你提到你也在普林斯顿大学。当时Andrew Wiles也在那里当教授,他宣布证明了费马大定理。现在回过头来看,有了更多关于那个数学历史时刻的背景,你当时是怎么想的?
陶哲轩:嗯,当时我是研究生。我依稀记得当时有媒体报道,我们的信箱都在同一个邮件室,突然Andrew Wiles的信箱里塞满了信件。
我们都在茶话会上讨论过,但我们不明白。我们大多数人基本上没理解那个证明,我们理解的是高层细节。事实上,Kevin Buzzard有一个正在进行的项目要在 Lean 中形式化它。
Lex Fridman:我们能稍微偏离一下主题吗?那有多难?因为据我所知,费马大定理的证明涉及非常复杂的东西。
陶哲轩:是的,现在要将其形式化真的很难。他们使用的对象是可以定义的,他们已经在 Lean 中定义过了,所以定义是可以做到的。这确实不是件简单的事,但它已经完成了。但是关于这些对象还有很多非常基本的事实,在所有这些不同的数学论文中花了数十年时间才得以证明,所有这些都需要形式化。
Kevin Buzzard有一个为期五年的资助来形式化费马大定理,他的目标是他认为自己可能无法一直追溯到基本公理,但他希望形式化到只需要依赖黑盒,即当时一些理论家在 1980 年就已经知道的东西,然后其他人或其他工作可以从那里继续进行。
这与我所熟悉的数学领域不同。在我研究的分析学中,我们研究的对象更贴近基础。我研究像素数、函数等至少在高中数学教育范围内可以定义的东西。但随后,数论中存在一个非常高级的代数分支,人们已经在这个领域构建了结构,而且是一个非常稳固的结构。至少在基础层面,它已经非常成熟,有相应的教科书等等。
但确实存在这样的情况:如果你没有经过这些年的学习,而想了解这个结构的第六层在发生什么,你必须花费大量时间,他们才能让你达到能够看到你所熟悉的东西的程度。
Lex Fridman:关于Andrew Wiles的经历,有哪些方面让你感到启发,正如我们之前谈论的,他七年的大部分时间都是秘密工作?
陶哲轩:这多少符合人们对数学家浪漫化的想象,在人们把数学家都想象成这些有点古怪的法师之类的人物时,这确实加强了这种观点。他做出了伟大的成就,而且他解决问题的风格与我自己的风格非常不同,这很棒。我们需要这样的人。
Lex Fridman:你能谈谈这个么?比如在合作方面?
陶哲轩:如果一个问题太难,我就喜欢放弃,但我们需要那些有毅力和无畏精神的人。我曾与这样的人合作,我想放弃,因为我们尝试的第一个方法没有成功,第二个也没有成功。但他们坚信,并且有第三、第四和第五个方法,最终成功了。而我不得不承认,“好吧,我原本认为这不会成功,但没错,你一直是对的。”
人类并非天生就拥有数学中心
Q:对于那些不了解情况的人来说,你不仅因工作的卓越而闻名,还因惊人的生产力而著称。所以,能不能谈谈你在不同领域之间转换的独到之处?
陶哲轩:在不同领域之间转换对我是很有效的,但也有一些人非常高效,他们能专注深入。
我认为每个人都需要找到自己的工作流程。数学中令人遗憾的一点是,数学在教学方法上似乎有一种适合所有人的方式,有一套特定的课程等等。如果你参加数学竞赛或类似的活动,你也许会获得略有不同的体验。
但我认为许多人,他们直到很晚,甚至通常是太晚,才找到自己的数学母语。所以他们会放弃数学,并且对试图用他们不喜欢的方式教他们数学的老师有不好的体验。
我的理论是,人类并非天生就拥有数学中心,进化并没有直接赋予我们大脑的数学中心。我们拥有视觉中心、语言中心以及其他一些进化中完善了的功能中心,但我们并没有天生的数学直觉。
然而我们的其他中心足够复杂,使我们能够将大脑的其他区域用于数学活动。因此,有些人已经掌握了如何利用视觉中心进行数学思考,在数学思考时会非常依赖视觉;有些人则改造了他们的语言中心,以非常符号化的方式思考;还有些人,如果他们非常具有竞争性并且喜欢玩游戏,大脑中有一部分非常擅长解决谜题和游戏,这部分也可以被改造用于数学。
但是当我和其他数学家谈论时,他们并不完全这样认为,我能看出他们使用的是其他不同的思维方式,这些方式并非相互排斥,但他们可能更偏爱视觉化。我其实并不那么偏爱视觉化,我自己也需要很多视觉辅助工具。但数学提供了一个通用语言,所以即使我们思考的方式不同,我们仍然能够相互交流。
Q:你能看出思考过程中使用的是不同的系统吗?
陶哲轩:是的,人们走不同的路径。他们在我感到困难的事情上非常迅速,反之,但我们仍然能达到同一个目标。
但我们的教育方式——除非你有个性化的导师或类似的东西——教育作为某种金融技能必须大规模生产。你必须用同一种方式教 30 个孩子,哪怕他们有 30 种不同的风格,你不能用 30 种不同的方式来教。
对年轻人的建议
Q:对于那些在数学上苦苦挣扎,但对数学感兴趣并希望变得更好的年轻学生,你对他们有什么建议吗?
陶哲轩:这是一个棘手的问题。好消息是,现在课堂之外有很多丰富的数学拓展资源。在我那个年代,就已经有数学竞赛,图书馆里也有通俗数学读物。现在还有YouTube、一些专门解决数学难题的论坛。
数学也出现在其它地方,例如一些扑克牌爱好者会对具体的概率问题感兴趣,实际上在扑克、国际象棋和棒球领域,都有一群业余概率论爱好者群体。
数学无处不在,我希望通过Lean这类新工具,可以将更广泛的公众纳入数学研究项目,当然目前还没有发生。
在科学领域,公民科学也有一定的空间,比如天文学中有业余爱好者发现了彗星、生物学中有人能识别蝴蝶。在数学方面,业余数学家也可以发现新素数。
但在以前,我们必须验证每一个贡献,就像大多数数学研究项目那样,来自公众的意见其实帮助不大,甚至事实上,那只会耗费时间,因为光是查错就很麻烦。
但现在形式化项目的好处是,它们正在聚集、吸纳更多人参与其中。所以我敢肯定,有些高中生已经为其中一些形式化项目做出了贡献,现在你不需要成为博士,就可以研究原子问题。
而编程则更容易进入,你可以执行代码并得到结果,很快就能打印出“Hello World”。如果把编程当作一门完全理论的学科来教,你只学计算机科学、函数理论、例程等,除了专门的家庭作业以外,你实际上不会在周末为了好玩而去编程,它们会被认为和数学一样难。
所以正如我所说,有一些非数学家群体,他们为了某些特定目的而运用数学,例如优化他们的扑克游戏策略,对他们而言,数学就变得有趣了。
Q:你对年轻人整体上有什么建议,例如如何选择职业、找到自我和擅长的东西?
陶哲轩:我认为你需要适应和灵活,获得可转移的技能,比如学习一种特定的编程语言或一门特定的数学学科或其它东西。其实这本身并不是完全可迁移,但可以从中知道如何用抽象概念进行推理,或者在出现问题时如何解决问题。这些都是我认为,即使在我们能使用的工具越来越好的情况下,即使你在AI支持下工作,我们仍然需要掌握的东西。
而我一直对数学的新方法感兴趣,因为我认为我们现在很多做事的方式都是低效的。我的很多同事,都花费了很多时间在做非常常规的计算上,或者是其他科学家知道怎么做但我们不知道的事情,为什么我们不能直接搜索并快速得到回应呢?这就是为什么我一直对探索新的工作流程很感兴趣。
大约四五年前,我在一个委员会里,我们需要为数学研究所征集一些举办有趣研讨会的想法。当时,Peter Scholze刚刚确立了他的一项新定理,计算机辅助证明方面也有一些其它的进展,看起来相当有趣。
我说,我们应该为此举办一个研讨会,这会是一个好主意。然后因为我对这个想法过于热情,我被要求去实践它。我和Kevin Buzzard、Jordan Ellenberg以及其他一些人一起做了,这是一次相当成功的研讨会。我们把一群数学家、计算机科学家和其他人聚集在一起,了解了最新的进展和状态。
这些进展非常有趣,但大多数科学家都不知道这些进展正在进行,还有很多很好的概念得以验证,是对一些即将发生的事情的暗示。这些都发生在ChatGPT出现之前,其实那时,也有一场关于语言模型及其未来潜在能力的演讲。这让我为之感到兴奋,于是我开始做报告,希望应该有更多人开始关注这个领域。
而就在这个会议举办之后,ChatGPT出现了,然后突然间AI无处不在。我接受了大量关于这个主题的采访,特别是有关AI和形式化证明辅助之间的互动。我说是的,它们应该结合起来,这里存在完美的协同效应。
然后在某个时刻,我意识到自己应该身体力行,而不只是口头说说而已。因为我既不在机器学习领域工作,也不在证明形式化领域工作,我仅仅只能靠权威发言,以知名数学家的身份让人们相信这将改变数学,但这是有限度的,尤其是当我自己一点都没有参与其中的时候,所以我认为我必须亲自实践来证明它。
实际上,我投入的很多事情,我都没有事先预料我将花费多少时间在上面,只有当我深陷某一个项目中时,我才意识到,我已经投入了太多。
如今数学如此庞大,没有人能了解所有的现代数学。不可避免的我们会犯错,但你不能仅用虚张声势来掩盖错误,因为人们会要求看你的证明,如果没有证明,那就是没有。
数学要求我们保持诚实,虽然这并不万能,但我们确实有一种倾向于承认错误的文化,因为我们总是被迫如此。
有史以来最伟大的数学家
Q:你认为谁是有史以来最伟大的数学家?
陶哲轩:首先,这取决于时间。如果你随着时间的累积来看,欧几里得是主要竞争者之一,然后在那之前是一些不知名的匿名数学家,无论是谁提出了数字的概念。
Lex Fridman:现在的数学家们还能感受到希尔伯特的影响吗?
陶哲轩:是的,直接影响,20世纪发生的所有事情都直接受其影响。例如希尔伯特空间,我们有很多东西都是以他的名字命名的,光是数学的体系安排,以及某些概念的引入。其中23个问题极具影响力。
这里存在无处不在的旁观者效应。如果没有人说你应该做X,那么每个人都只是四处走动,等待别人做某事,但实际什么也没做。
所以实际上,你必须教会数学本科生的是,你应该总是尝试去做一些事情。所以你会看到他们尝试数学问题时总会陷入瘫痪,如果他们意识到某种技巧可以应用,他们就会尝试,但他们也看到了一些问题,标准技巧已经明显不适用的情况下,他们就会无从下手,不知道该做什么。
这让我想起一句辛普森一家的名言:“我什么都没尝试,但我完全不知道怎么办了。”所以,要知道下一步就是尝试任何事情,无论多么愚蠢,甚至注定会失败,你也会从失败方式中得到启发。比如失败是因为你完全没有考虑过这个假设,那么这个假设一定有用,这就是一个线索。
Q:您能详细说一下之前提过的一个叫做结构化拖延法的方法吗?当你不想做一件事时,去想象一件比这更糟糕的事情,然后以不做更糟糕的事情来拖延,这是一个很有效的技巧。
陶哲轩:是的,对于任何事情,心理学都很重要。当你和马拉松运动员交谈时,他们谈论的最重要的事情不是训练方案或饮食,而在很大程度上是心理,只要自我欺骗相信问题是可行的,这样你就会有动力去做它。
Q:是否存在我们人类大脑永远无法理解的东西?
陶哲轩:作为数学家,根据归纳法,一定存在足够大的数字,而我们无法理解,这是我首先能想到的。
Lex Fridman:那么集体智慧可行吗?
陶哲轩:是的,我认为复数意义上的人类,原则上在状态好时,拥有比单个个体总和更多的智慧。当然它也可能更少。
复数意义上的数学共同体是一个令人难以置信的超级智能体,没有任何单个的人类数学家能与之匹敌。有时你能看到在数学社区中,对于非常困难的问题,能够迅速给出快速的答案。作为专家,旁观这个过程实际上是种享受。
Q:对于人类文明的整个过程,是什么让你充满希望?
陶哲轩:我认为年轻一代总是非常有创造力、热情和发明力。和年轻学生一起工作是一种乐趣。要知道科学的进步告诉我们,过去非常困难的问题,现在变得非常容易解决。
比如说导航,了解自己在地球上的位置,这曾经是个非常可怕的问题,人们因此丧命或者倾家荡产,但现在我们口袋里的设备就能自动帮我们做到,这已经不再是问题。现在对于我们来说,似乎不可行的事情,只有可能是家庭作业练习。
Lex Fridman:是的,所以我总是对生命的有限性感到悲哀,我们无法看到我们作为一个文明创造的所有酷炫事物。
陶哲轩:现在已经发生了很多事情,如果能够回到过去,和十几岁的自己交谈,或者仅仅是让互联网和现在的人工智能交谈,它们都已经逐渐被内化。你会理所当然地认为AI可以听懂我们说话,并对任何问题给出合理的或者稍微有点错误的答案。但这在两年前,还是令人震惊的。
Lex Fridman:在当下看着互联网上的各种反应,这种戏剧性场面也很有趣。人们很快就把一切都视为理所当然,然后我们人类似乎能用任何自己创造出来的东西,自娱自乐。有人持一种观点,另一个人需要持相反观点,然后为此争论不休。但是当你退后一步看待事情的轨迹时,即使是机器人技术的进步,也会感叹人类的创造力。
陶哲轩:是的。当基础设施和文化健康时,人类共同体可以比其中的个体更聪明、成熟和理性得多。
Lex Fridman:没错,在有一个地方,我总是能够看到理性,那就是您博客的评论区,那里汇集了很多非常聪明的人。好的,最后非常感谢您抽出时间接受访谈。
陶哲轩:谢谢,这是我的荣幸。
Lex Fridman:最后请让我引用伽利略的一句话为本次访谈收尾:
数学是上帝用来书写宇宙的一种语言。

参考链接:
[1]https://lexfridman.com/terence-tao-transcript
[2]https://www.youtube.com/watch?v=HUkBz-cdB-k
[3]https://github.com/teorth/equational_theories
[4]https://arxiv.org/abs/math/0211159
—完—



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


