建筑生破解60年数学悬案，制成「永远同一面朝上」的单稳四面体
闻乐 时令 发自 凹非寺 量子位 | 公众号 QbitAI
扔100次，99次「同一面朝上」。
这个由碳纤维和碳化钨（航空材料）打造的“几何怪物”，竟破解了60年数学悬案。
添加图片注释，不超过 140 字（可选）
如果这个发明早一点出现，或许“雅典娜”月球着陆器也不会一侧翻就躺平了（doge）。
早在1966年，数学家约翰·康威和他的搭档查德·盖伊提出了“均匀单稳态四面体”构想。
他们想利用均匀材料制作一个重量分布均匀的四面体，无论将这个四面体如何放置，它总会翻到稳定的那一面朝上。
几年后，这对搭档通过不断尝试，否定了均匀单稳四面体的猜想：这是不存在的。
但是，如果让重量分配不均匀呢？
后来，康威猜测不均匀配重的单稳四面体应该存在，但他未发表任何证明。
半个世纪以后，这个数学猜想由建筑学者杰尔戈·阿尔马迪“跨界”证实，还制作出了实物。
所以，这位建筑学者是如何在数学问题上大展身手的呢？
从连续曲面到尖顶多面体
伟大的数学家约翰·康威对多四面体的排列和平衡方式非常感兴趣。
于是，他和搭档想要构建一个由均匀材料制成的四面体——其重量均匀分布，无论如何翻滚，最终总会翻到其稳定的一面。
很遗憾的是，他们在长达几年的研究之后发现，这种均匀单稳四面体是不存在的。
这时，康威转变了原来的想法：如果允许模型配重不均匀，那这样的单稳四面体存在吗？
这个问题就像是在陀螺玩具下面装上一个重物，似乎是可行的。
但有人认为，这种解决方法只适用于光滑形状的物体，对于多面体来说可能并不合适。
康威认为这种四面体应该存在，但他没有发表过任何证明。
并且，他本人更专注于研究更高维度、均匀重量的四面体的平衡问题，所以不均匀单稳四面体的探索在数十年来并没有得到广泛关注。
直到2006年，数学家多莫科斯和其同事发现了 “gömböc” 形状。
这种形状有一个非常不寻常的特点——单稳态。
如果随意抛掷，它始终会翻滚到其平衡点上。
它只在两个点上保持平衡，但一个稳定，另一个不稳定，就像硬币的圆面和侧面一样。
添加图片注释，不超过 140 字（可选）
但“gömböc”的某些地方是圆的，它是一个连续曲面而非多面体，多莫科斯想知道一个尖顶多面体是否也能具有类似的特性。
因此康威的猜想引起了他的兴趣。
于是，多莫斯科和他的团队开始踏上了探索单稳四面体之路。
直到他的一个学生出现，值得注意的是，这个学生本身还不是学数学的。
借助计算机发现单稳四面体
这个学生就是阿尔马迪，他是在多莫科斯的一个选修课上接触到了这个问题。
2022年，阿尔马迪作为一名建筑专业的学生选修了多莫科斯的力学课程。
学期末，多莫科斯让他设计一个简单的算法，探索四面体如何平衡。
与康威时代用纸和笔进行计算不同，几十年后的阿尔马迪已经有了计算机作为辅助。
于是，他利用计算机穷举搜索大量可能的形状。
最终，阿尔马迪的算法程序找到了一个四面体四个顶点的坐标，当配备具体重量时，这个四面体就具有了单稳态性质。
这证明康威的猜想是对的。
然而，具有这种性质的四面体只有一个吗？还有没有其他符合条件的四面体？它们之间有什么共性呢？
带着这些问题，团队利用计算机开始了更深层次的探索。
他们意识到，要让四面体实现单稳态，其三条相连的边（即两个面相交的地方）必须构成钝角，且质心必须落在四个“加载区”之一。
简单来说，加载区就是单稳四面体内部的四个小四面体区域。
当四面体倾倒时，质心会向支撑面的一侧移动，如果质心始终处于该面所对应的加载区内，则重力作用下，会使四面体始终稳定在该面上，若质心超出加载区，四面体就可能会翻到其他面。
理论已经证明了单稳四面体存在，那么这个结构能用真实材料制作出来吗？
团队模拟了单稳四面体从倾倒到稳定的路径。
通过计算得出需要用密度约为太阳核心1.5倍的材料构建形状的一部分。
添加图片注释，不超过 140 字（可选）
后来，他们找到了一个更可行的方式，设计了一个大部分是空心的四面体。由轻质的碳纤维框架构成，其中一小部分由碳化钨制成。
为了让较轻的部分尽可能轻，即使是碳纤维框架也必须是空心的。
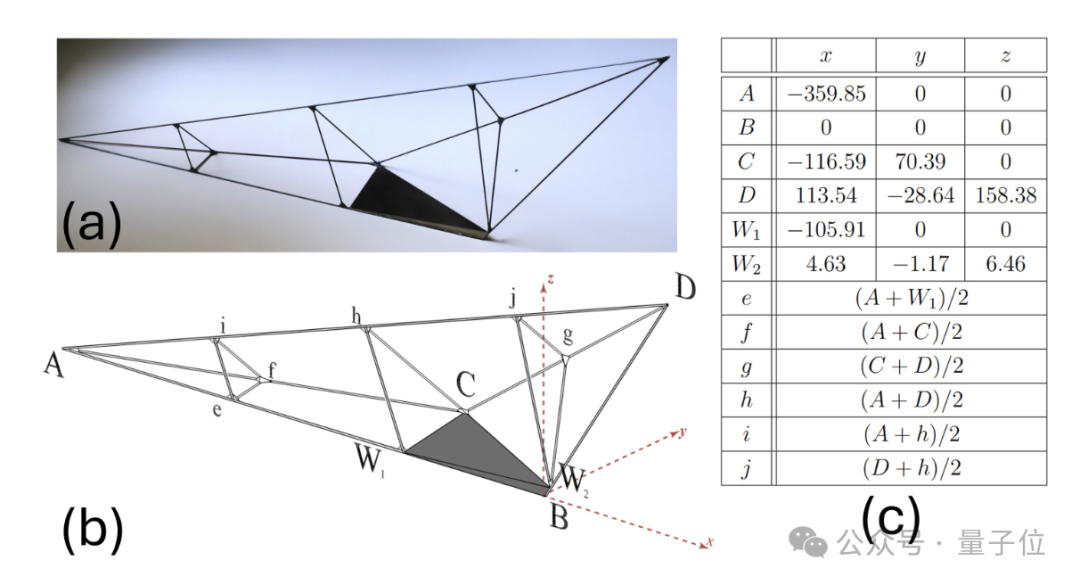
添加图片注释，不超过 140 字（可选）
经过精密制造与高昂投入，多莫科斯团队终于完成模型，却发现它无法按照理论进行翻滚。
直到某天，多莫科斯和总工程师发现模型其中一个顶点上粘着一个胶水团。
他们请技术员把它清理掉，20分钟后，阿尔马迪收到了多莫科斯的短信：“它工作了。”
这让正在散步的阿尔马迪开始在街上跳来跳去，他兴奋地表示：
“我们设计了它，而且它有效，这真是太棒了！”
从手动解题到计算机辅助
单稳四面体猜想的提出者约翰·康威专注于研究高维度几何平衡问题。
快速计算是康威的一个标志性特质。
1970年，康威在一篇论文中提出了一种更高效的方法来完成同样的工作，据说，他只用了一个下午的时间。
他的方法被称为“康威记号”，这种方法使得绘制“结”中的缠结和重叠变得容易很多。
曾有人说，他是唯一一个能用自己双手解决问题的数学家，无需借助工具就能达成让人惊叹的成就。
△约翰·康威
而在几十年后，人们有了计算机来辅助解决复杂问题。
建筑学者阿尔马迪“跨界”解决数学问题离不开计算机的辅助。
添加图片注释，不超过 140 字（可选）
正如网友所说，这个单稳四面体的形状是由计算机计算并且筛选出的。
如果没有计算机帮忙搜索，或许这个问题还将持续下一个60年。
添加图片注释，不超过 140 字（可选）
在完成这项数学工作后，阿尔马迪还幽默地表示：
“我原本想成为一名建筑师，为什么会在这里？”
答案或许是因为计算机～
目前，多莫斯科与阿尔马迪正致力于将这个成果迁移到航空工作中，比如设计翻倒后能自动恢复正面的月球着陆器。
添加图片注释，不超过 140 字（可选）
论文地址：https://arxiv.org/abs/2506.19244 参考链接： [1]https://www.quantamagazine.org/a-new-pyramid-like-shape-always-lands-the-same-side-up-20250625/ [2]https://news.ycombinator.com/item?id=44381297 [3]https://www.quantamagazine.org/john-conway-solved-mathematical-problems-with-his-bare-hands-20200420/
—完—
版权所有，未经授权不得以任何形式转载及使用，违者必究。
正文完
可以使用微信扫码关注公众号（ID：xzluomor）
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
tornado crypto mixer
Discover the power of privacy with TornadoCash! Learn how this decentralized mixer ensures your transactions remain confidential.
ดูบอลสด
Very well presented. Every quote was awesome and thanks for sharing the content. Keep sharing and keep motivating others.
ดูบอลสด
Pretty! This has been a really wonderful post. Many thanks for providing these details.
ดูบอลสด
Pretty! This has been a really wonderful post. Many thanks for providing these details.
ดูบอลสด
Hi there to all, for the reason that I am genuinely keen of reading this website’s post to be updated on a regular basis. It carries pleasant stuff.
Obrazy Sztuka Nowoczesna
Thank you for this wonderful contribution to the topic. Your ability to explain complex ideas simply is admirable.
ufabet
Hi there to all, for the reason that I am genuinely keen of reading this website’s post to be updated on a regular basis. It carries pleasant stuff.
ufabet
Very well presented. Every quote was awesome and thanks for sharing the content. Keep sharing and keep motivating others.